
Karakteristiske egenskaber, fordele og ulemper ved metoden med lav pris

Det laveste omkostningsmetode er en procedure, der anvendes til at opnå den indledende mulige løsning på et transportproblem. Anvendes, når prioriteten er at reducere produktdistributionsomkostningerne.
Metoden med den laveste pris søger at opnå de laveste transportomkostninger mellem flere efterspørgselscentre (destinationerne) og flere forsyningscentre (kilderne)..

Produktions- eller forsyningskapaciteten for hver kilde samt behovet eller efterspørgslen fra hver destination er kendt og fast..
Omkostningerne ved at transportere en enhed af produktet fra hver kilde til hver destination er også kendt..
Produktet skal transporteres fra forskellige kilder til forskellige destinationer på en sådan måde, at det imødekommer efterspørgslen fra hver destination og samtidig minimerer de samlede transportomkostninger..
Andre metoder kan bruges, hvis prioriteten er tidsbesparelser snarere end omkostningsbesparelser.
Artikelindeks
- 1 Funktioner
- 1.1 Trin til den laveste omkostningsmetode
- 1.2 Anvendelser
- 2 fordele
- 3 ulemper
- 4 Eksempel
- 4.1 Forklaring af metoden
- 5 Referencer
Egenskaber
Den optimale fordeling af et produkt fra forskellige kilder til forskellige destinationer kaldes et transportproblem..
- Transportmodeller beskæftiger sig med transport af et produkt fremstillet i forskellige fabrikker eller fabrikker (forsyningskilder) til forskellige lagre (efterspørgselsmål).
- Formålet er at opfylde kravene til destinationerne inden for fabrikkernes produktionskapacitetsbegrænsninger til de minimale transportomkostninger..
Trin til den laveste omkostningsmetode
Trin 1
Den celle, der indeholder de laveste transportomkostninger i hele tabellen, vælges. Denne celle tildeles så mange enheder som muligt. Denne mængde kan være begrænset af begrænsninger i udbud og efterspørgsel..
I tilfælde af at flere celler har de laveste omkostninger, vælges den celle, hvor den maksimale tildeling kan foretages.
Derefter fortsætter vi med at justere udbud og efterspørgsel i den berørte række og kolonne. Det justeres ved at trække det beløb, der er tildelt cellen.
Trin 2
Den række eller søjle, hvor udbuddet eller efterspørgslen er opbrugt (det være sig nul), elimineres.
Hvis begge værdier, udbud og efterspørgsel, er lig med nul, kan enhver række eller kolonne elimineres vilkårligt.
Trin 3
De foregående trin gentages med de næste laveste omkostninger og fortsætter, indtil alt tilgængeligt tilbud i de forskellige kilder eller al efterspørgsel fra de forskellige destinationer er opfyldt..
Ansøgninger
- Minimer transportomkostningerne fra fabrikker til lagre eller fra lager til detailbutikker.
- Bestem den laveste prisplacering for en ny fabrik, lager eller salgskontor.
- Bestem produktionsplanen for mindstepriser, der imødekommer virksomhedens efterspørgsel med produktionsbegrænsninger.
Fordel
Den laveste omkostningsmetode anses for at give mere nøjagtige og optimale resultater sammenlignet med det nordvestlige hjørne.
Dette skyldes, at metoden med det nordvestlige hjørne kun tager højde for kravet om levering og tilgængelighed med det øverste venstre hjørne som startgodtgørelse uanset forsendelsesomkostninger..
På den anden side inkluderer metoden med laveste omkostninger transportomkostninger, mens der foretages opgaver..
- I modsætning til den nordvestlige hjørne-metode giver denne metode en nøjagtig løsning, da den tager hensyn til transportomkostningerne ved kortlægning.
- Den billigste metode er en meget enkel metode at bruge.
- Det er meget simpelt og let at beregne den optimale løsning med denne metode.
- Den billigste metode er meget let at forstå.
Ulemper
- For at opnå den optimale løsning skal visse regler følges. Imidlertid følger metoden med den laveste pris ikke trin for trin.
- Den laveste omkostningsmetode følger ikke systematiske regler, når der er uafgjort i de laveste omkostninger.
- Den billigste metode giver mulighed for udvælgelse gennem medarbejderobservation, hvilket kan skabe misforståelser for at opnå den optimale løsning.
- Det har ikke evnen til at tilvejebringe nogen form for kriterier til at bestemme, om løsningen opnået med denne metode er den mest optimale..
- Mængderne af tilbud og krav er altid de samme, da de ikke varierer over tid..
- Det tager ikke hensyn til andre typer faktorer at tildele, men kun transportomkostningerne.
Eksempel
Konceptet med den laveste omkostningsmetode kan forstås gennem følgende problem:
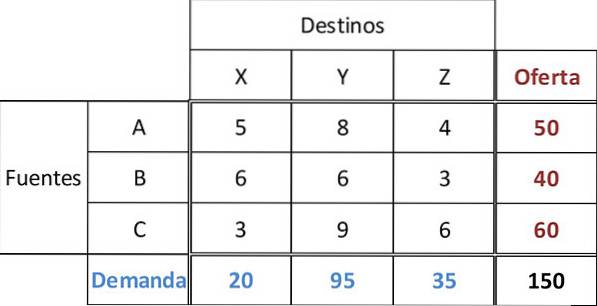
I denne tabel er forsyningen af hver kilde A, B, C henholdsvis 50, 40 og 60 enheder. Efterspørgslen fra de tre forhandlere X, Y, Z er henholdsvis 20, 95 og 35 enheder. For alle ruter angives transportomkostningerne.
Minimumsomkostningerne ved transport kan opnås ved at følge nedenstående trin:
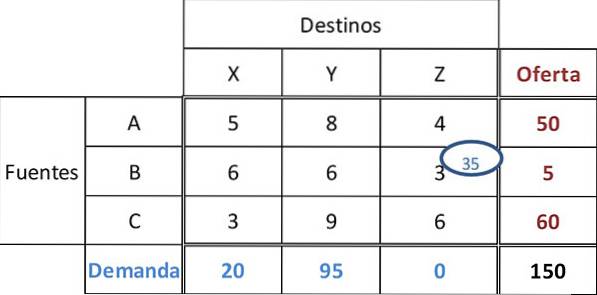
Minimumsomkostningerne i tabellen er 3 med uafgjort i cellerne BZ og CX. Generelt skal omkostningerne vælges, hvor det største beløb kan tildeles for at opnå den bedste indledende løsning.
Derfor tildeles 35 enheder til celle BZ. Dette tilfredsstiller efterspørgslen fra forhandler Z og efterlader 5 enheder i kilde B.
Forklaring af metoden
Igen er minimumsomkostningerne 3. Derfor tildeles 20 enheder til celle CX. Dette opfylder efterspørgslen fra forhandler X og efterlader 40 enheder i kilde C.
Den næste minimumomkostning er 4. Efterspørgslen efter Z er imidlertid allerede afsluttet. Vi går til den næste minimumomkostning, som er 5. Også efterspørgslen efter X er allerede afsluttet.
Den næste minimumomkostning er 6 med uafgjort mellem tre celler. Du kan dog ikke tildele enheder til cellerne BX og CZ, fordi efterspørgslen fra detailhandlerne X og Z er opfyldt. Derefter tildeles 5 enheder til celle BY. Dette afslutter levering af kilde B.
Den næste minimumomkostning er 8 ved at tildele 50 enheder til celle AY og afslutte levering fra kilde A.
Den næste minimumomkostning er 9. 40 enheder tildeles celle CY, hvorved efterspørgslen og udbuddet til alle destinationer og kilder fuldføres. Den resulterende endelige opgave er:
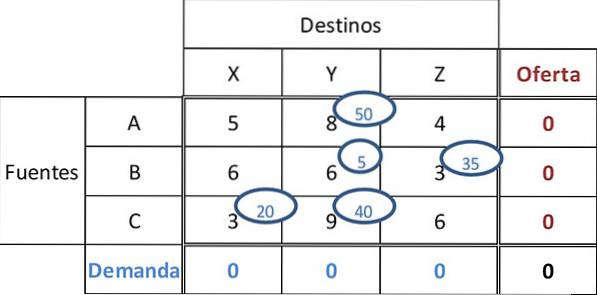
De samlede omkostninger kan beregnes ved at multiplicere de tildelte beløb med omkostningerne i de tilsvarende celler: Samlede omkostninger = 50 * 8 + 5 * 6 + 35 * 3 + 20 * 3 + 40 * 9 = 955.
Referencer
- Forretningsjargoner (2019). Mindste omkostningsmetode. Hentet fra: businessjargons.com.
- Opdragsrådgivning (2019). Hjælp til tildeling af mindste omkostningsmetode. Hentet fra: assignmentconsultancy.com.
- Forretningsstyring (2015). Transportproblem. Hentet fra: engineering-bachelors-degree.com.
- Josefina Pacheco (2019). Hvad er den laveste omkostningsmetode? Web og virksomheder. Hentet fra: webyempresas.com.
- Atozmath (2019). Eksempel på mindste omkostningsmetode. Hentet fra: cbom.atozmath.com.



Endnu ingen kommentarer