Definition af centripetalacceleration, formler, beregning, øvelser

Det centripetal acceleration til_c, Også kaldet radial eller normal, det er accelerationen, som en bevægende genstand bærer, når den beskriver en cirkulær sti. Dens størrelse er v^to/ r, hvor r er cirkelens radius, den er rettet mod midten af ​​den og er ansvarlig for at holde mobilen på vej.

Dimensionerne på centripetalacceleration er længde pr. Tidsenhed i kvadrat. I det internationale system er de m / s^to. Hvis centripetalaccelerationen af ​​en eller anden grund forsvinder, forsvinder også kraften, der tvinger mobilen til at opretholde den cirkulære sti.

Dette er hvad der sker med en bil, der prøver at svinge på et fladt, iskoldt spor, hvor friktionen mellem jorden og hjulene er utilstrækkelig til, at bilen kan svinge. Derfor er den eneste mulighed, der er tilbage, at bevæge sig i en lige linje, og det er derfor, det forlader kurven.

Artikelindeks

• 1 Cirkulære bevægelser
• 2 Den centripetale kraft
• 3 Formler til centripetal acceleration
• 4 Øvelse løst
  • 4.1 Svar
• 5 Referencer

Cirkulære bevægelser

Når en genstand bevæger sig i en cirkel, er den centripetale acceleration til enhver tid rettet radialt mod centrum af omkredsen, en retning, der er vinkelret på den fulde sti.

Da hastighed altid er tangent til stien, viser hastighed og centripetal acceleration at være vinkelret. Derfor har hastighed og acceleration ikke altid samme retning.

Under disse omstændigheder har mobilen mulighed for at beskrive omkredsen med konstant eller variabel hastighed. Den første sag er kendt som Uniform Circular Movement eller MCU for dens akronym, den anden sag vil være en variabel cirkulær bevægelse.

I begge tilfælde er centripetalacceleration ansvarlig for at holde mobilen roterende og sikre, at hastigheden kun varierer i retning og i retning.

For at have en variabel cirkulær bevægelse er der imidlertid brug for en anden komponent i accelerationen i samme retning af hastigheden, som har ansvaret for at øge eller mindske hastigheden. Denne komponent af acceleration er kendt som tangentiel acceleration.

Variabel cirkulær bevægelse og kurvlinær bevægelse generelt har begge komponenter i acceleration, fordi kurvlinær bevægelse kan forestilles som stien gennem utallige perifere buer, der udgør den buede sti..

Den centripetale kraft

Nu er en styrke ansvarlig for at levere accelerationen. For en satellit, der kredser om jorden, er det tyngdekraften. Og da tyngdekraften altid virker vinkelret på banen, ændrer den ikke satellitens hastighed..

I et sådant tilfælde fungerer tyngdekraften som en centripetal kraft, som ikke er en særlig eller separat kraftklasse, men som i satellitens tilfælde er rettet radialt mod centrum af jorden.

I andre typer cirkulær bevægelse, for eksempel en bil, der drejer en kurve, spilles centripetalkraftens rolle af statisk friktion, og for en sten bundet til et reb, der roteres i cirkler, er spændingen i rebet den kraft, der tvinger mobil til spin.

Formler til centripetal acceleration

Centripetalacceleration beregnes ved udtrykket:

ac = v^to/ r

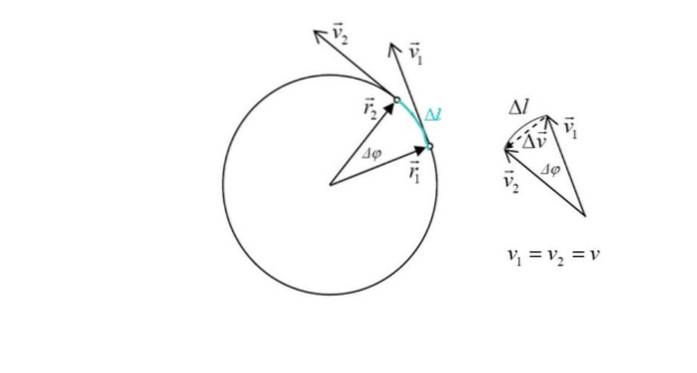
Dette udtryk afledes nedenfor. Per definition er acceleration ændringen i hastighed over tid:

Mobilen tager tid Δt i ruten, som er lille, da punkterne er meget tætte.

Figuren viser også to positionsvektorer r₁ Y r_to, hvis modul er det samme: radius r af omkredsen. Vinklen mellem de to punkter er Δφ. I grønt fremhæver sløjfe krydset af mobilen, betegnet som Δl.

I figuren til højre ses det, at størrelsen af ​​Δv, ændringen i hastighed er nogenlunde proportional med Δl, da vinklen Δφ er lille. Men hastighedsændringen er nøjagtigt relateret til acceleration. Fra trekanten kan det ses ved at tilføje vektorer, der:

v₁ + Δv = v_to → Δv = v_to - v₁

Δv det er interessant, da det er proportionalt med centripetal acceleration. Fra figuren kan det ses, at da vinklen Δφ er lille, er vektoren Δv er i det væsentlige vinkelret på begge dele v₁ synes godt om v_to og peger på midten af ​​omkredsen.

Selvom vektorerne indtil nu er fremhævet med fed skrift, for virkningerne af en geometrisk natur, der følger, arbejder vi med modulerne eller størrelsen af ​​disse vektorer, undgår vi vektortegningen.

Noget andet: du skal bruge definitionen af ​​central vinkel, som er:

Δφ= Δl / r

Nu sammenlignes begge figurer, som er proportionale siden vinklen Δφ det er normalt:

Opdeling efter Δt:

til_c= v^to/ r

Træning løst

En partikel bevæger sig i en cirkel med en radius på 2,70 m. På et givet øjeblik er dens acceleration 1,05 m / s^to i en retning, der udgør en vinkel på 32,0º med bevægelsesretningen. Beregn din hastighed:

a) På det tidspunkt

b) 2,00 sekunder senere, forudsat konstant tangentiel acceleration.

Svar

Det er en varieret cirkulær bevægelse, da udsagnet indikerer, at accelerationen har en given vinkel med bevægelsesretningen, der hverken er 0 ° (det kan ikke være en cirkulær bevægelse) eller 90 ° (det ville være en ensartet cirkulær bevægelse).

Derfor eksisterer de to komponenter - radial og tangential - sammen. De vil blive betegnet som en_c allerede_t og er tegnet i følgende figur. Vektoren i grønt er nettoaccelerationsvektoren eller simpelthen acceleration til.

a) Beregning af accelerationskomponenterne

til_c = a.cos θ = 1,05 m / s^to . cos 32,0º = 0,89 m / s^to (i rødt)

til_t = a.sen θ = 1,05 m / s^to . sin 32,0º = 0,57 m / s^to (i orange)

Beregning af mobilens hastighed

Siden en_c = v^to/ r, derefter:

v = v_eller +til_t. t = 1,6 m / s + (0,57 x 2) m / s = 2,74 m / s

Referencer

1. Giancoli, D. Fysik. 2006. Principper med applikationer. Sjette udgave. Prentice Hall. 107-108.
2. Hewitt, Paul. 2012. Konceptuel fysik. Femte udgave.Pearson.106-108.