Det aksiomer af sandsynlighed de er matematiske udsagn, der henviser til teorien om sandsynlighed, som ikke fortjener bevis. Axiomerne blev etableret i 1933 af den russiske matematiker Andrei Kolmogorov (1903-1987) i sit arbejde Grundlæggende om sandsynlighedsteori og lagde grundlaget for den matematiske undersøgelse af sandsynligheden.
Når du udfører et bestemt tilfældigt eksperiment ξ, er prøveområdet E sættet med alle mulige resultater af eksperimentet, også kaldet begivenheder. Enhver begivenhed betegnes som A og P (A) er sandsynligheden for dens forekomst. Derefter fastslog Kolmogorov, at:
-Axiom 1 (ikke negativitet): sandsynligheden for, at en begivenhed A finder sted, er altid positiv eller nul, P (A) ≥0. Når sandsynligheden for en begivenhed er 0, kaldes den umulig begivenhed.
-Axiom 2 (sikkerhed): hver gang en begivenhed, der hører til E, er dens sandsynlighed for forekomst 1, som vi kan udtrykke som P (E) = 1. Det er det, der er kendt som en sikker begivenhed, da der med al sikkerhed er et resultat, når man gennemfører et eksperiment.
-Axiom 3 (tilføjelse): i tilfælde af to eller flere inkompatible begivenheder to og to, kaldet A1, TILto, TIL3…, Sandsynligheden for, at begivenhed A forekommer1 plus Ato plus A3 og så videre er det summen af sandsynlighederne for, at hver enkelt sker separat.
Dette udtrykkes som: P (A1 U Ato U A3 U…) = P (A1) + P (A.to) + P (A.3) + ...
Artikelindeks
Sandsynlighedsaksiomerne anvendes i vid udstrækning i en lang række applikationer. For eksempel:
En tommelfingerstang eller stød kastes i luften, og når den falder på gulvet, er der mulighed for at lande med punktet op (U) eller med punktet ned (D) (vi overvejer ikke andre muligheder). Eksempelrummet for dette eksperiment består af disse begivenheder, derefter E = U, D.
Ved at anvende aksiomerne har vi:
P (E) = 1 (Axiom 2)
Men P (E) = P (U) + P (D) (Axiom 3), fordi disse begivenheder er gensidigt uforenelige eller uensartede. Tommelfingeren falder ikke med spidsen op eller ned på samme tid, den er den ene eller den anden, men ikke begge, da andre muligheder ikke overvejes. Derefter:
P (U) + P (D) = 1
P (U) = 1 - P (D)
Uanset om det er lige så sandsynligt, at det lander spids op eller peger nedad, P (U) = P (D) = ½ (Axiom 1). Det kan dog være, at konstruktionen og designet af thumbtack er mere tilbøjelige til at falde på den ene eller anden måde. For eksempel kan det være det P (U) = ¾ mens P (D) = ¼ (Axiom 1).
Bemærk, at summen af sandsynlighederne i begge tilfælde giver 1. Axiomerne angiver dog ikke, hvordan sandsynlighederne skal tildeles, i det mindste ikke fuldstændigt. Men de bekræfter, at de er tal mellem 0 og 1, og at som i dette tilfælde er summen af alle 1.
Sandsynlighedens aksiomer er ikke en metode til at tildele sandsynlighedsværdien. Til dette er der tre muligheder, der er kompatible med aksiomerne:
Hver begivenhed tildeles den samme sandsynlighed for at ske, så er sandsynligheden for forekomst defineret som:
P (A) = antal sager, der er gunstige for begivenhed A / antal mulige sager
For eksempel, hvad er sandsynligheden for at trække et es fra en bunke franske kort? Bunken har 52 kort, 13 af hver kulør, og der er 4 dragter. Hver dragt har 1 ess, så i alt er der 4 ess:
P (som) = 4/52 = 1/13
Laplace's regel er begrænset til begrænsede prøvepladser, hvor hver begivenhed er lige sandsynlig.
Her skal eksperimentet kunne gentages, da metoden er baseret på at udføre et stort antal gentagelser..
Lad os lave gentagelser af eksperimentet ξ, hvoraf vi finder ud af, at n er antallet af gange, hvor en bestemt begivenhed A forekommer, så sandsynligheden for, at denne begivenhed opstår, er:
P (A) = limi → ∞ (ingen af dem)
Hvor n / i er den relative hyppighed af en begivenhed.
Definition af P (A) på denne måde tilfredsstiller Kolmogorovs aksiomer, men har den ulempe, at mange tests skal udføres for at sandsynligheden er passende.
En person eller en gruppe mennesker kan blive enige om at tildele sandsynligheden for en begivenhed gennem deres egen vurdering. Denne metode har den ulempe, at forskellige mennesker kan tildele forskellige sandsynligheder til den samme begivenhed..
I eksperimentet med samtidig at kaste 3 ærlige mønter skal du opnå sandsynligheden for de beskrevne begivenheder:
a) 2 hoveder og en hale.
b) 1 hoved og to haler
c) 3 kryds.
d) Mindst 1 ansigt.
Hoved er betegnet med C og haler med X. Men der er flere måder at få to hoveder og en hale på. For eksempel kan de to første mønter lande hoveder og den tredje kan haler. Eller det første kan falde hoveder, det andet haler og det tredje hoveder. Og endelig kan den første være haler og de resterende hoveder.
For at besvare spørgsmålene er det nødvendigt at kende alle de muligheder, der er beskrevet i et kaldet værktøj trædiagram eller sandsynlighedens træ:
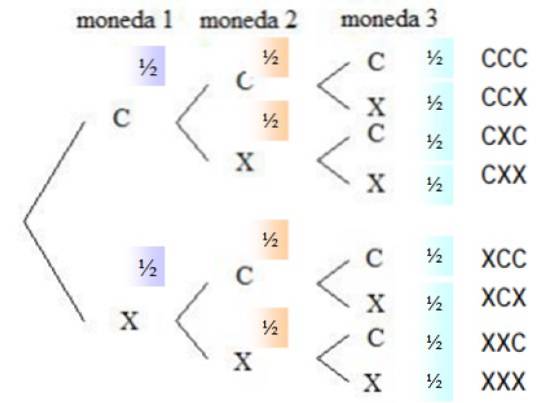
Sandsynligheden for, at en mønt kommer ud af hovederne, er ½, det samme gælder haler, da mønten er ærlig. I højre kolonne vises alle de muligheder, som kastet har, dvs. prøveområdet.
Fra prøveområdet vælges de kombinationer, der reagerer på den anmodede begivenhed, da rækkefølgen, som ansigterne vises i, ikke er vigtig. Der er tre gunstige begivenheder: CCX, CXC og XCC. Sandsynligheden for, at hver begivenhed sker, er:
P (CCX) = ½. ½. ½ = 1/8
Det samme sker for CXC og XCC begivenhederne, hver har en 1/8 sandsynlighed for at ske. Derfor er sandsynligheden for at få nøjagtigt 2 hoveder summen af sandsynligheden for alle gunstige begivenheder:
P (2-sidet) = 1/8 + 1/8 + 1/8 = 3/8 = 0,375
At finde sandsynligheden for, at nøjagtigt to kryds forekommer, er et problem analogt med det foregående, der er også tre gunstige begivenheder taget fra prøveområdet: CXX, XCX og XXC. Derfor:
P (2 kryds) = 3/8 = 0,375
Intuitivt ved vi, at sandsynligheden for at få 3 haler (eller 3 hoveder) er lavere. I dette tilfælde er den søgte begivenhed XXX i slutningen af højre kolonne, hvis sandsynlighed er:
P (XXX) = ½. ½. ½ = 1/8 = 0,125.
Det anmodes om at opnå mindst 1 ansigt, det betyder, at 3 ansigter, 2 ansigter eller 1 ansigt kan komme ud. Den eneste begivenhed, der er uforenelig med dette, er den, hvor 3 haler kommer ud, hvis sandsynlighed er 0,125. Derfor er den ønskede sandsynlighed:
P (mindst 1 hoved) = 1 - 0,125 = 0,875.
Endnu ingen kommentarer