Frit faldskoncept, ligninger, løste øvelser

Det frit fald det er den lodrette bevægelse, som et objekt oplever, når det falder fra en bestemt højde tæt på jordens overflade. Det er en af ​​de enkleste og mest øjeblikkelige bevægelser, der er kendt: i en lige linje og med konstant acceleration.

Alle genstande, der tabes, eller som kastes lodret op eller ned, bevæger sig med accelerationen på 9,8 m / s^to leveret af jordens tyngdekraft, uanset dens masse.

I dag kan denne kendsgerning accepteres uden problemer. Men at forstå den sande natur af frit fald tog et stykke tid. Grækerne havde allerede beskrevet og fortolket det på en meget grundlæggende måde i det 4. århundrede f.Kr..

Artikelindeks

• 1 Bevægelsesligninger for frit fald
  • 1.1 Kinematiske mængder
  • 1.2 Hastighed som en funktion af forskydning
• 2 Eksempler på frit fald
  • 2.1 Acceleration
  • 2.2 Position som funktion af tid: y (t)
  • 2.3 Hastighed som funktion af tid: v (t)
  • 2.4 Hastighed som en funktion af forskydning
  • 2.5 Det lodrette kaste op
• 3 Løst øvelser
  • 3.1 Øvelse 1
  • 3.2 Øvelse 2
• 4 Referencer

Ligninger med frit fald bevægelse

Når først overbevist om, at accelerationen er den samme for alle kroppe, der frigøres under tyngdekraften, er det tid til at etablere de ligninger, der er nødvendige for at forklare denne bevægelse..

Det er vigtigt at understrege, at der ikke tages højde for luftmodstand i denne første bevægelsesmodel. Resultaterne af denne model er dog meget nøjagtige og tæt på virkeligheden..

I alt det følgende antages partikelmodellen, det vil sige objektets dimensioner tages ikke i betragtning, forudsat at al massen er koncentreret i et enkelt punkt.

For en ensartet accelereret retlinet bevægelse i lodret retning tages y-aksen som referenceakse. Den positive retning tages opad og den negative retning nedad..

De kinematiske størrelser

På denne måde er ligningerne af position, hastighed og acceleration som en funktion af tiden:

Acceleration

a = g = -9,8 m / s^to (-32 ft / s^to)

Position som en funktion af tiden: og T)

y = y_eller + v_eller . t + ½ gt^to

Hvor og_eller er mobilens startposition og v_eller er den indledende hastighed. Husk, at i lodret opadkast er starthastigheden nødvendigvis forskellig fra 0.

Som kan skrives som:

og - og_eller = v_eller . t + ½ gt^to

Δy = v_eller . t + ½ gt^to

Med ΔY er den forskydning, der udføres af den mobile partikel. I enheder af det internationale system er både position og forskydning angivet i meter (m).

Hastighed som en funktion af tiden: v (t)

v = v_eller + g. t

Hastighed som en funktion af forskydning

Det er muligt at udlede en ligning, der forbinder forskydningen med hastigheden uden tid at gribe ind i den. Til dette ryddes tidspunktet for den sidste ligning:

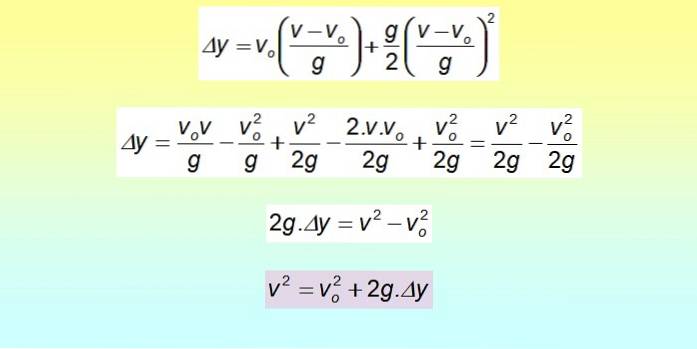
Δy = v_eller . t + ½ gt^to

Pladsen er udviklet ved hjælp af det bemærkelsesværdige produkt, og vilkårene omgrupperes.

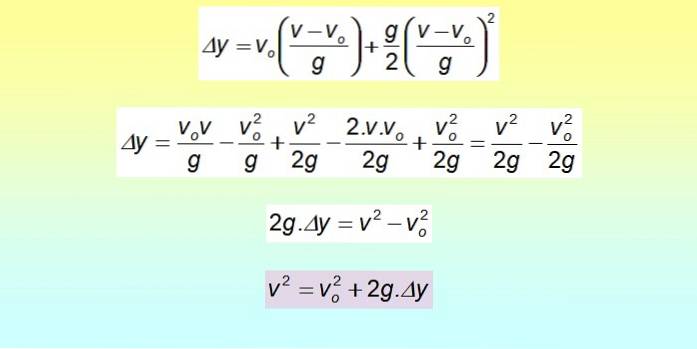
Denne ligning er nyttig, når du ikke har tid, men i stedet har du hastigheder og forskydninger, som du vil se i afsnittet om løste eksempler..

Eksempler på frit fald

Den opmærksomme læser vil have bemærket tilstedeværelsen af ​​den indledende hastighed v_eller. De foregående ligninger er gyldige for lodrette bevægelser under tyngdekraften, både når objektet falder fra en bestemt højde, og hvis det kastes lodret op eller ned.

Når objektet tabes, gøres det simpelthen v_eller = 0 og ligningerne forenkles som følger.

Acceleration

a = g = -9,8 m / s^to (-32 ft / s^to)

Position som en funktion af tiden: og T)

y = y_eller+ ½ gt^to

Hastighed som en funktion af tiden: v (t)

v = g. t

Hastighed som en funktion af forskydning

v^to = 2 g. D y

D y vil også være negativ, da v^to det skal være en positiv mængde. Dette vil ske, uanset om du tager kilde eller nul koordinatsystem ved startpunktet eller på jorden.

Hvis læseren foretrækker det, kan han tage den nedadgående retning som positiv. Tyngdekraften vil fortsætte med at handle, hvis det menes at være + 9,8 m / s^to. Men du skal være i overensstemmelse med den valgte tegnkonvention.

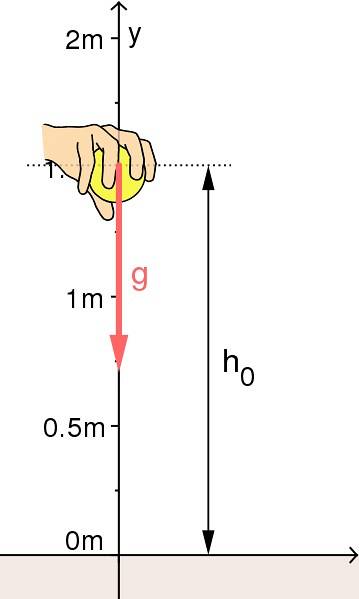
Det lodrette kast op

Her kan selvfølgelig starthastigheden ikke være nul. Du er nødt til at give objektet en impuls til at stige. I henhold til den angivne starthastighed vil objektet stige til en større eller mindre højde.

Selvfølgelig vil der være et øjeblik, når objektet stopper et øjeblik. Derefter er den maksimale højde fra startpunktet nået. Ligeledes er accelerationen stadig g nedad. Lad os se, hvad der sker i dette tilfælde.

Beregning af den maksimale nåede højde

Valg af i = 0:

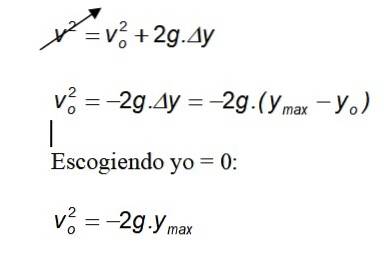
Da tyngdekraften altid peger på jorden i negativ retning, annulleres det negative tegn.

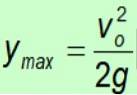
Beregning af den maksimale tid

En lignende procedure bruges til at finde den tid, det tager for objektet at nå den maksimale højde.

v = v_eller + g. t

Det gør det v = 0

v_eller = - g. t_maks

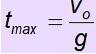
Flyvetid er, hvor længe objektet varer i luften. Hvis objektet vender tilbage til startpunktet, er stigningstiden lig med nedstigningstiden. Derfor er flyvetiden 2. t maks.

Er det to gange t_maks den samlede tid, objektet varer i luften? Ja, så længe objektet starter fra et punkt og vender tilbage til det.

Hvis lanceringen foretages fra en bestemt højde over jorden, og objektet får lov til at fortsætte mod den, vil flyvetiden ikke længere være dobbelt så lang tid.

Løst øvelser

I opløsningen af ​​de følgende øvelser overvejes følgende:

1-Højden, hvorfra objektet tabes, er lille sammenlignet med jordens radius.

2-luftmodstand er ubetydelig.

3-Værdien af ​​tyngdeacceleration er 9,8 m / s^to

4-Når det kommer til problemer med en enkelt mobil, vælges det fortrinsvis og_eller = 0 ved startpunktet. Dette gør normalt beregninger lettere..

5-Medmindre andet er angivet, betragtes den lodrette opadgående retning som positiv.

6-I de kombinerede stigende og faldende bevægelser tilbyder ligningerne, der anvendes direkte de korrekte resultater, så længe konsistensen med tegnene opretholdes: opadgående positiv, nedadgående negativitet og tyngdekraft -9,8 m / s^to eller -10 m / s^to hvis afrunding foretrækkes (for nemheds skyld ved beregning).

Øvelse 1

En kugle kastes lodret opad med en hastighed på 25,0 m / s. Svar på følgende spørgsmål:

a) Hvor højt gør det?

b) Hvor lang tid tager det at nå dit højeste punkt?

c) Hvor lang tid tager det for bolden at røre jordens overflade, når den når sit højeste punkt?

d) Hvad er din hastighed, når du vender tilbage til det niveau, hvorfra du startede?

Opløsning

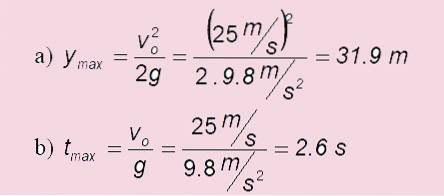
c) I tilfælde af en planstart: t_flyvningen = 2. t_maks = 2 x6 s = 5,1 s

d) Når den vender tilbage til startpunktet, har hastigheden samme størrelse som den oprindelige hastighed, men i den modsatte retning, derfor skal den være - 25 m / s. Det kontrolleres let ved at erstatte værdier i ligningen for hastighed:

Øvelse 2

En lille postpose frigives fra en helikopter, der falder ned med en konstant hastighed på 1,50 m / s. Efter 2,00 s beregnes:

a) Hvad er kuffertens hastighed?

b) Hvor langt er kufferten under helikopteren?

c) Hvad er dine svar på del a) og b) hvis helikopteren stiger med en konstant hastighed på 1,50 m / s?

Opløsning

Punkt a

Når du forlader helikopteren, bærer posen derfor starthastigheden på helikopteren v_eller = -1,50 m / s. Med den angivne tid er hastigheden steget takket være tyngdeacceleration:

v = v_eller + g. t = -1,50 - (9,8 x 2) m / s = - 21,1 m / s

Afsnit b

Lad os se, hvor meget kufferten er faldet fra startpunktet på det tidspunkt:

Kuffert: Dy = v_eller . t + ½ gt^to = -1,50 x 2 + ½ (-9,8) x 2^to m = -22,6 m

Er valgt Y_eller = 0 ved startpunktet, som angivet i begyndelsen af ​​afsnittet. Det negative tegn angiver, at kufferten er faldet 22,6 m under startpunktet..

I mellemtiden helikopteren Det er faldet med en hastighed på -1,50 m / s antager vi med konstant hastighed, derfor har helikopteren på den angivne tid på 2 sekunder rejst:

Helikopter: Δy = v_eller.t = -1,50 x 2 m = -3 m.

Derfor adskilles kufferten og helikopteren efter 2 sekunder med en afstand på:

d =| -22,6 - (-3) | m = 19. 6 m.

Afstand er altid positiv. For at fremhæve denne kendsgerning anvendes den absolutte værdi.

Afsnit c

Når helikopteren stiger, har den en hastighed på + 1,5 m / s. Med den hastighed kommer kufferten ud, så den efter 2 s allerede har:

v = v_eller + g. t = +1,50 - (9,8 x 2) m / s = - 18,1 m / s

Hastigheden viser sig at være negativ, da posen efter 2 sekunder bevæger sig nedad. Det er steget takket være tyngdekraften, men ikke så meget som i afsnit a.

Lad os nu finde ud af, hvor meget kufferten er kommet ned fra startpunktet i løbet af de første 2 sekunders rejse:

Taske: Δy = v_eller . t + ½ gt^to = +1,50 x 2 + ½ (-9,8) x 2^to m = -16,6 m

I mellemtiden er helikopteren er opstået med hensyn til startpunktet og har gjort det med konstant hastighed:

Helikopter: Δy = v_eller.t = +1,50 x 2 m = +3 m.

Efter 2 sekunder adskilles kufferten og helikopteren med en afstand på:

d =| -16,6 - (+3) | m = 19,6 m

Den afstand, der adskiller dem, er den samme i begge tilfælde. Kufferten bevæger sig mindre lodret i det andet tilfælde, fordi dens indledende hastighed blev rettet opad..

Referencer

1. Kirkpatrick, L. 2007. Fysik: Et blik på verden. 6^ta Forkortet udgave. Cengage læring. 23 - 27.
2. Rex, A. 2011. Grundlæggende fysik. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14^th. Red. Bind 1. 50 - 53.
4. Serway, R., Vulle, C. 2011. Fundamentals of Physics. 9^na Ed. Cengage Learning. 43 - 55.
5. Wilson, J. 2011. Fysik 10. Pearson Education. 133 - 149.