
Chi-kvadrat (χ²) fordeling, hvordan man beregner det, eksempler
Beviset Chi i firkant eller chi-firkant (χto, hvor χ er det græske bogstav kaldet "chi") bruges til at bestemme opførelsen af en bestemt variabel, og også når du vil vide, om to eller flere variabler er statistisk uafhængige.
For at kontrollere en variabels opførsel kaldes den test, der skal udføres chi kvadrat test af pasform. For at finde ud af om to eller flere variabler er statistisk uafhængige, kaldes testen chi firkant af uafhængighed, også kaldet beredskab.
Disse tests er en del af den statistiske beslutningsteori, hvor en population undersøges, og der træffes beslutninger om den og analyserer en eller flere prøver taget fra den. Dette kræver, at der antages visse antagelser om de kaldte variabler hypotese, hvilket måske eller måske ikke er sandt.
Der er nogle tests, der kontrasterer disse formodninger og bestemmer, hvilke gyldighed der er inden for en vis tillidsmargin, herunder chi-kvadrat-testen, som kan anvendes til at sammenligne to og flere populationer..
Som vi vil se, hæves to typer hypoteser normalt omkring en populationsparameter i to prøver: nullhypotesen kaldet Heller (prøverne er uafhængige) og den alternative hypotese betegnet som H1, (prøverne er korreleret) hvilket er det modsatte af det.
Artikelindeks
- 1 Hvornår anvendes chi-kvadrat-testen?
- 1.1 Betingelser for at anvende det
- 2 Chi firkantet fordeling
- 2.1 Grader af frihed
- 2.2 Formulering af hypoteser
- 3 Hvordan beregnes chi-kvadratstatistikken?
- 3.1 Acceptkriterier for Ho
- 4 Beregningseksempel
- 5 Referencer
Hvornår bruges chi-kvadrat-testen?
Chi-kvadrat-testen anvendes på variabler, der beskriver kvaliteter, såsom køn, civilstand, blodgruppe, øjenfarve og præferencer af forskellige typer.
Testen er beregnet, når du vil:
-Kontrol af, om en distribution er passende til at beskrive en variabel, der kaldes godhed af pasform. Ved hjælp af chi-kvadrat-testen er det muligt at vide, om der er signifikante forskelle mellem den valgte teoretiske fordeling og den observerede frekvensfordeling..
-Ved, om to variabler X og Y er uafhængige af det statistiske synspunkt. Dette er kendt som uafhængighedstest.
Da den anvendes på kvalitative eller kategoriske variabler, bruges chi-kvadrat-testen i vid udstrækning inden for samfundsvidenskab, ledelse og medicin..
Betingelser for at anvende det
Der er to vigtige krav for at anvende det korrekt:
-Dataene skal grupperes i frekvenser.
-Prøven skal være stor nok til, at chi-kvadratfordelingen er gyldig, ellers er dens værdi overvurderet og fører til afvisning af nulhypotesen, når det ikke skulle være tilfældet..
Den generelle regel er, at hvis en frekvens med en værdi mindre end 5 vises i de grupperede data, bruges den ikke. Hvis der er mere end en frekvens mindre end 5, skal de kombineres til en for at opnå en frekvens med en numerisk værdi større end 5.
Chi kvadratfordeling
χto det er en kontinuerlig fordeling af sandsynligheder. Der er faktisk forskellige kurver, afhængigt af en parameter k hedder grader af frihed af den tilfældige variabel.
Dens egenskaber er:
-Arealet under kurven er lig med 1.
-Værdierne for χto de er positive.
-Fordelingen er asymmetrisk, det vil sige den har en bias.
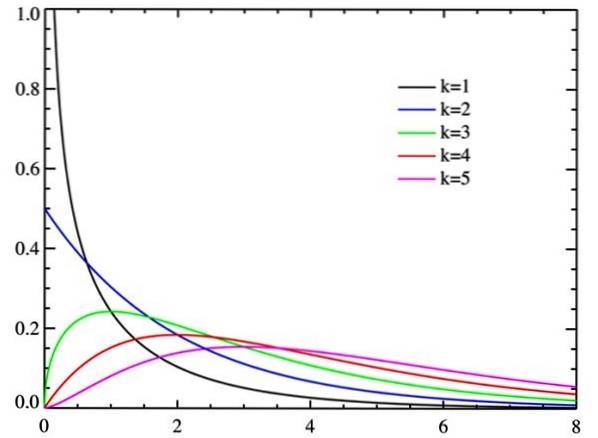
Grader af frihed
Når frihedsgraderne stiger, har chi-kvadratfordelingen en tendens til normalitet, som det kan ses af figuren.
For en given fordeling bestemmes frihedsgraderne gennem beredskabstabel, hvilket er tabellen, hvor de observerede frekvenser af variablerne registreres.
Hvis et bord har F rækker og c kolonner, værdien af k det er:
k = (f - 1) ⋅ (c - 1)
Formulering af hypoteser
Når chi-kvadrat-testen er passende, formuleres følgende hypoteser:
-Heller: variablen X har en sandsynlighedsfordeling f (x) med de specifikke parametre y1, Yto…, Ys
-H1: X har en anden sandsynlighedsfordeling.
Sandsynlighedsfordelingen antaget i nulhypotesen kan for eksempel være den kendte normalfordeling, og parametrene ville være gennemsnittet μ og standardafvigelsen σ.
Derudover evalueres nulhypotesen med et vist niveau af betydning, det vil sige et mål for den fejl, der ville blive begået, når den afvises, at den er sand.
Normalt er dette niveau indstillet til 1%, 5% eller 10%, og jo lavere det er, desto mere pålideligt er testresultatet..
Og hvis den chi-kvadratiske test af beredskab anvendes, som, som vi har sagt, tjener til at verificere uafhængigheden mellem to variabler X og Y, er hypoteserne:
-Heller: variabler X og Y er uafhængige.
-H1: X og Y er afhængige.
Igen er det nødvendigt at specificere et niveau af betydning for at kende størrelsen på fejlen, når man træffer beslutningen..
Hvordan beregnes chi-kvadratstatistikken?
Statistikken for chi-kvadrat beregnes som følger:

Summationen udføres fra første klasse i = 1 til den sidste, hvilket er i = k.
Hvad mere er:
-Feller er en observeret frekvens (kommer fra de opnåede data).
-Fog er den forventede eller teoretiske frekvens (skal beregnes ud fra dataene).
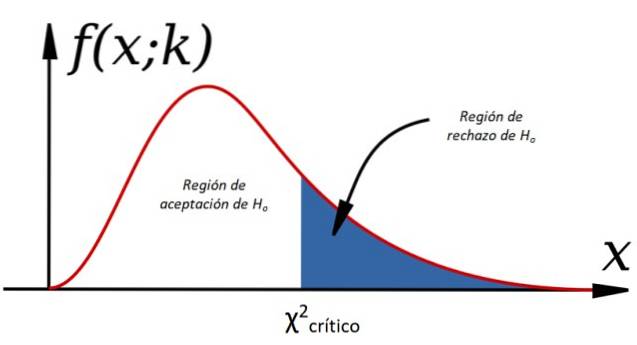
For at acceptere eller afvise nulhypotesen beregner vi χto for de observerede data og sammenlignet med en kaldet værdi kritisk chi-firkant, hvilket afhænger af frihedsgraderne k og niveauet af betydning a:
χtokritisk = χtok, α
Hvis vi for eksempel vil udføre testen med et signifikansniveau på 1%, så er α = 0,01, hvis det vil være med 5%, så er α = 0,05 og så videre. Vi definerer p, fordelingsparameteren, som:
p = 1 - a
Disse kritiske chi kvadratværdier bestemmes af tabeller, der indeholder den kumulative arealværdi. For eksempel for k = 1, der repræsenterer 1 frihedsgrad og α = 0,05, hvilket er lig med p = 1- 0,05 = 0,95, er værdien afto er 3.841.

H acceptkriteriereller
Kriteriet for accept af Heller det er:
-Ja χto < χtokritisk H acceptereseller, ellers afvises det (se figur 1).
Beregningseksempel
I den følgende applikation vil chi kvadrat test bruges som en test af uafhængighed.
Antag, at forskerne vil vide, om præferencen for sort kaffe er relateret til personens køn, og specificer svaret med et signifikansniveau på α = 0,05.
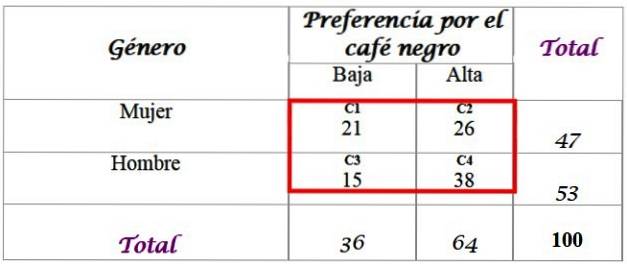
Til dette er der et stikprøve på 100 personer, der er interviewet, og deres svar er tilgængelige:
Trin 1
Fastlæg hypoteserne:
-Heller: køn og præference for sort kaffe er uafhængige.
-H1: smagen til sort kaffe er relateret til personens køn.
Trin 2
Beregn de forventede frekvenser for fordelingen, for hvilke totalerne tilføjet i sidste række og i højre kolonne i tabellen er påkrævet. Hver celle i det røde felt har en forventet værdi Fog, som beregnes ved at multiplicere summen af din række F med summen af din kolonne C, divideret med summen af prøven N:
Fog = (F x C) / N
Resultaterne er som følger for hver celle:
-C1: (36 x 47) / 100 = 16,92
-C2: (64 x 47) / 100 = 30,08
-C3: (36 x 53) / 100 = 19,08
-C4: (64 x 53) / 100 = 33,92
Trin 3
Dernæst skal chi-kvadratstatistikken beregnes for denne fordeling i henhold til den givne formel:

Trin 4
Bestem χtokritisk, vel vidende at de registrerede data er i f = 2 rækker og c = 2 kolonner, derfor er antallet af frihedsgrader:
k = (2-1) ⋅ (2-1) = 1.
Hvilket betyder, at vi skal se i værdien χ i tabellen ovenfortok, α = χto1; 0,05 , som er:
χtokritisk = 3.841
Trin 5
Sammenlign værdierne og beslut:
χto = 2.9005
χtokritisk = 3.841
Siden χto < χtokritisk nulhypotesen accepteres, og det konkluderes, at præferencen for sort kaffe ikke er knyttet til personens køn med et signifikansniveau på 5%.
Referencer
- Chi Square Test for uafhængighed. Gendannet fra: saylordotorg.github.io.
- Med Wave. Statistikker anvendt på sundhedsvidenskab: chi-kvadrat-testen. Gendannet fra: medwave.cl.
- Sandsynligheder og statistikker. Chi-square godhed-af-fit test. Gendannet fra: probayestadistica.com.
- Triola, M. 2012. Elementær statistik. 11. Udgave. Addison Wesley.
- UNAM. Chi kvadrat test. Gendannet fra: asesorias.cuautitlan2.unam.mx.


Endnu ingen kommentarer