
Carnot cyklus faser, applikationer, eksempler, øvelser
Det Carnot cyklus det er sekvensen af termodynamiske processer, der finder sted i en Carnot-motor, en ideel enhed, der kun består af reversible typeprocesser; det vil sige dem, der har fundet sted, kan vende tilbage til den oprindelige tilstand.
Denne type motor betragtes som ideel, da den mangler spredning, friktion eller viskositet, der opstår i virkelige maskiner, der omdanner termisk energi til brugbart arbejde, selvom konverteringen ikke udføres 100%.

En motor er bygget ud fra et stof, der er i stand til at udføre arbejde, såsom gas, benzin eller damp. Dette stof udsættes for forskellige temperaturændringer og oplever igen variationer i dets tryk og volumen. På denne måde er det muligt at flytte et stempel inde i en cylinder.
Artikelindeks
- 1 Hvad er carnot-cyklussen?
- 2 faser af Carnot-cyklussen
- 2.1 Udgangspunkt
- 2.2 Første fase: isoterm ekspansion
- 2.3 Anden fase: adiabatisk ekspansion
- 2.4 Tredje trin: isoterm kompression
- 2.5 Fjerde fase: adiabatisk kompression
- 3 Carnots sætning
- 3.1 Bevis for Carnots sætning
- 3.2 Konsekvens af sætning og begrænsninger
- 4 eksempler
- 4.1 Et stempel inde i en cylinder
- 4.2 Forskellige reversible processer
- 4.3 Et atomkraftværk
- 5 Øvelser løst
- 5.1-Eksempel 1: effektivitet af en varmemotor
- 5.2-Eksempel 2: absorberet varme og varmeoverført
- 6 Referencer
Hvad er carnot-cyklussen?
Carnot-cyklussen finder sted i et system kaldet Carnot-motoren eller C, som er en ideel gas indesluttet i en cylinder og forsynet med et stempel, der er i kontakt med to kilder ved forskellige temperaturer T1 og Tto som den, der er vist i nedenstående figur til venstre.
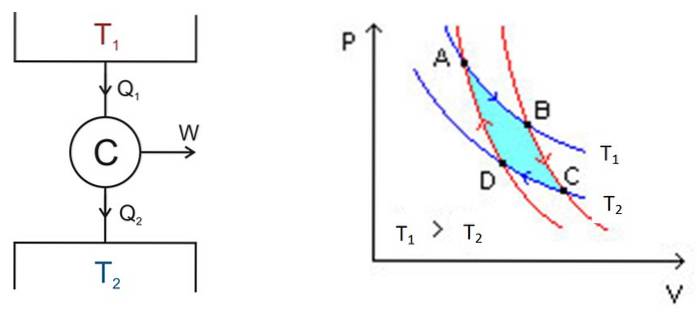
Der finder følgende grove processer sted:
- En bestemt mængde varme tilføres enheden Qindgang = Q1 fra den termiske tank ved høj temperatur T1.
- Carnots motor C udfører arbejde W takket være denne tilførte varme.
- En del af den anvendte varme: affaldet QAfslut, overføres til den termiske tank, som har en lavere temperatur Tto.
Faser af Carnot-cyklussen
Analysen udføres ved hjælp af et PV-diagram (tryk-volumen), som vist i figur 2 (højre figur). Formålet med motoren kan være at holde det termiske reservoir 2 køligt og udvinde varme fra det. I dette tilfælde er det en køling maskine. Hvis du derimod ønsker at overføre varme til termisk tank 1, er det en varmepumpe.
P-V-diagrammet viser ændringerne i motorens tryk - temperatur under to forhold:
- Holde temperaturen konstant (isoterm proces).
- Ingen varmeoverførsel (varmeisolering).
De to isotermiske processer skal forbindes, hvilket opnås ved termisk isolering.
Punkt
Du kan starte når som helst i cyklussen, hvor gassen har visse betingelser for tryk, volumen og temperatur. Gassen gennemgår en række processer og kan vende tilbage til startbetingelserne for at starte en ny cyklus, og den endelige interne energi er altid den samme som den oprindelige. Da energi er bevaret:
Arbejde udført af C = varmeindgang - varmeydelse
ΔW = Qindgang - SpørgsmålAfslut
Området inden for denne sløjfe eller turkis i figuren svarer nøjagtigt til det arbejde, der udføres af Carnot-motoren.
I figur 2 markeres punkt A, B, C og D. Vi starter ved punkt A efter den blå pil..
Første fase: isoterm ekspansion
Temperaturen mellem punkterne A og B er T1. Systemet absorberer varme fra det termiske reservoir 1 og gennemgår en isoterm ekspansion. Derefter øges lydstyrken, og trykket falder.
Imidlertid forbliver temperaturen ved T1, siden når gassen udvider sig, køler den ned. Derfor forbliver dens interne energi konstant.
Anden fase: adiabatisk ekspansion
Ved punkt B begynder systemet en ny udvidelse, hvor systemet hverken vinder eller mister varme. Dette opnås ved at placere det i varmeisolering som angivet ovenfor. Derfor er det en adiabatisk udvidelse, der fortsætter med at pege C efter den røde pil. Volumen øges, og trykket falder til den laveste værdi.
Tredje trin: isoterm kompression
Det begynder ved punkt C og slutter ved D. Isoleringen fjernes, og systemet kommer i kontakt med termisk tank 2, hvis temperatur Tto er mindre. Systemet overfører spildvarme til det termiske reservoir, trykket begynder at stige, og lydstyrken falder.
Fjerde fase: adiabatisk kompression
Ved punkt D går systemet tilbage til varmeisolering, trykket stiger, og lydstyrken falder, indtil det når de oprindelige betingelser for punkt A. Derefter gentages cyklussen igen..
Carnots sætning
Carnots sætning blev først postuleret i det tidlige 19. århundrede af den franske fysiker Sadi Carnot. I 1824 udgav Carnot, som var en del af den franske hær, en bog, hvor han foreslog svaret på følgende spørgsmål: under hvilke betingelser har en varmemotor maksimal effektivitet? Carnot etablerede derefter følgende:
Ingen varmemotor, der kører mellem to varmebeholdere, er mere effektiv end Carnot-motoren.
Virkningsgraden η af en varmemotor gives af kvotienten mellem det udførte arbejde W og den absorberede varme Q:
ydeevne = udført arbejde / varme absorberet
På denne måde er effektiviteten af enhver varmemotor I: η = W / Q. Mens effektiviteten af en Carnot-motor R er η '= W / Q', forudsat at begge motorer er i stand til at udføre det samme arbejde.
Carnots sætning siger, at η aldrig er større end η '. Ellers falder det i modsætning til termodynamikens anden lov, ifølge hvilken en proces, hvor resultatet er, at varme kommer ud af en krop med lavere temperatur for at gå til en højere temperatur uden at modtage ekstern hjælp, er umulig. Derfor:
η < η''
Bevis for Carnots sætning
For at vise, at dette er tilfældet, skal du overveje Carnot-motoren, der fungerer som en kølemaskine, der drives af en I-motor. Dette er muligt, da Carnot-motoren fungerer ved reversible processer, som angivet i starten..
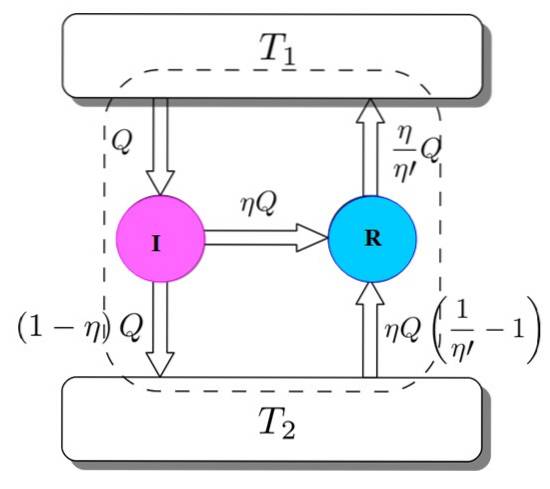
Vi har begge: I og R arbejder med de samme termiske reservoirer, og det antages, at η > η''. Hvis der undervejs opnås en modsigelse med den anden lov om termodynamik, bevises Carnos sætning ved reduktion til absurditet.
Figur 3 hjælper dig med at følge processen. Motoren I optager en mængde varme Q, som den deler på denne måde: udfører arbejde på R svarende til W = ηQ, og resten er den varme, der overføres (1-η) Q til det termiske reservoir Tto.
Da energi er bevaret, er alt af følgende sandt:
OGindgang = Q = Arbejd W + varme givet til Tto = ηQ + (1-η) Q = EAfslut
Nu tager Carnot-kølemaskinen R fra det termiske reservoir 2 en mængde varme givet af:
(η / η ') (1-η') Q =
I dette tilfælde skal der også spares energi:
OGindgang = ηQ + (η / η ') (1-η') Q = (η / η ') Q = Q' = EAfslut
Resultatet er overførslen til den termiske tank Tto af en varmemængde givet af (η / η ') Q = Q'.
Hvis η er større end η ', betyder det, at mere varme har nået den termiske aflejring ved højere temperatur, end jeg oprindeligt tog. Da ingen ekstern agent, såsom en anden varmekilde, har deltaget, er den eneste måde, der kan ske på, at det koldeste termiske reservoir opgiver varmen..
Dette er uenig med den anden lov om termodynamik. Derefter konkluderes det, at det ikke er muligt, at η'' er mindre end η, derfor kan motoren I ikke have mere effektivitet end Carnot-maskinen R.
Resultat af sætning og begrænsninger
Resultatet af Carnots sætning siger, at to Carnot-maskiner har samme effektivitet, hvis de begge arbejder med de samme termiske reservoirer..
Det betyder uanset stoffet, ydeevnen er uafhængig og kan ikke hæves ved at ændre den..
Konklusionen fra ovenstående analyse er, at Carnot-cyklussen er den ideelt opnåelige top af den termodynamiske proces. I praksis er der mange faktorer, der mindsker effektiviteten, for eksempel det faktum, at isoleringen aldrig er perfekt, og i de adiabatiske faser er der faktisk varmeudveksling med det udvendige.
I tilfælde af en bil bliver motorblokken varm. På den anden side opfører blandingen af benzin og luft sig ikke nøjagtigt som en ideel gas, hvilket er udgangspunktet for Carnot-cyklussen. Dette for kun at nævne et par faktorer, der vil medføre en drastisk reduktion i ydeevne.
Eksempler
Et stempel inde i en cylinder
Hvis systemet er et stempel indkapslet i en cylinder som i figur 4, stiger stemplet under isoterm ekspansion, som det kan ses i det første diagram yderst til venstre, og stiger også under adiabatisk ekspansion.
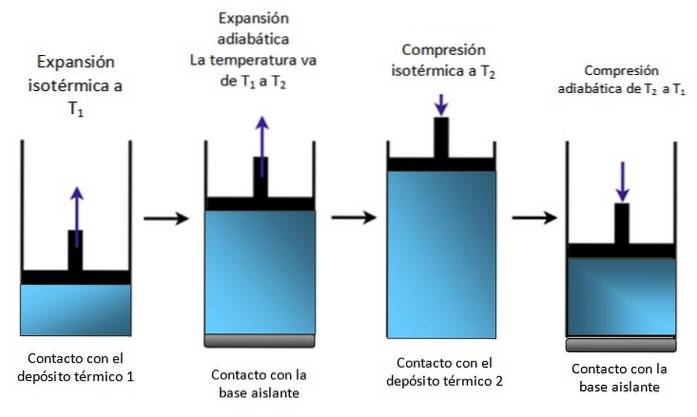
Derefter komprimeres den isotermt og giver varme og fortsætter med at komprimere adiabatisk. Resultatet er en bevægelse, hvor stemplet går op og ned inde i cylinderen, og som kan overføres til andre dele af en bestemt enhed, f.eks. En bilmotor, der producerer drejningsmoment eller en dampmaskine.
Forskellige reversible processer
Ud over udvidelsen og komprimeringen af en ideel gas inde i en cylinder er der andre ideelle reversible processer, hvormed en Carnot-cyklus kan konfigureres, for eksempel:
- Frem og tilbage bevægelser i mangel af friktion.
- En ideel fjeder, der komprimerer og dekomprimerer og aldrig deformeres.
- Elektriske kredsløb, hvor der ikke er nogen modstande til at sprede energi.
- Magnetiserings- og demagnetiseringscyklusser, hvor der ikke er tab.
- Opladning og afladning af et batteri.
Et atomkraftværk
Selv om det er et meget komplekst system, er en første tilnærmelse af hvad der kræves for at producere energi i en atomreaktor som følger:
- En termisk kilde, der består af et radioaktivt rådnende materiale såsom uran.
- Den kolde køleplade eller reservoir, der ville være atmosfæren.
- "Carnot-motoren", der bruger næsten altid vand fra hanen, til hvilken der tilføres varme fra den termiske kilde for at omdanne den til damp.
Når cyklussen udføres, opnås elektrisk energi som nettoarbejde. Når det omdannes til damp ved høj temperatur, bringes vandet til at nå en turbine, hvor energien omdannes til bevægelse eller kinetisk energi.
Turbinen driver igen en elektrisk generator, der omdanner energien fra dens bevægelse til elektrisk energi. Ud over fissilt materiale såsom uran kan fossile brændstoffer naturligvis bruges som varmekilde..
Løst øvelser
-Eksempel 1: effektivitet af en varmemotor
Effektiviteten af en varmemotor er defineret som kvotienten mellem outputarbejdet og inputarbejdet, og det er derfor en dimensionsløs størrelse:
Maksimal effektivitet = (Qindgang - Spørgsmål Afslut) / Qindgang
Angiver den maksimale effektivitet som emaks, det er muligt at demonstrere dets afhængighed af temperatur, som er den nemmeste variabel at måle, såsom:
ogmaks = 1 - (Tto/ T1)
Hvor Tto er sumptemperaturen og T1 er temperaturen på varmekilden. Da sidstnævnte er større, viser effektiviteten sig altid at være mindre end 1.
Antag at du har en varmemotor, der kan fungere på følgende måder: a) Mellem 200 K og 400 K, b) Mellem 600 K og 400 K. Hvad er effektiviteten i hvert enkelt tilfælde?
Opløsning
a) I det første tilfælde er effektiviteten:
ogmax1 = 1 - (200/400) = 0,50
b) I den anden tilstand er effektiviteten:
ogmax2 = 1- (400/600) = 0,33
Selvom temperaturforskellen er den samme mellem begge tilstande, er effektiviteten ikke. Og endnu mere bemærkelsesværdigt er, at den mest effektive tilstand fungerer ved en lavere temperatur..
-Eksempel 2: absorberet varme og frigivet varme
En 22% effektiv varmemotor producerer 1.530 J arbejde. Find: a) Den mængde varme, der absorberes fra den termiske tank 1, b) Den mængde varme, der udledes til den termiske tank 2.
a) I dette tilfælde anvendes definitionen af effektivitet, da det udførte arbejde er tilgængeligt, ikke temperaturerne på de termiske tanke. En effektivitet på 22% betyder, at e maks = 0,22, derfor:
Maksimal effektivitet = Arbejde / Qindgang
Mængden af absorberet varme er nøjagtigt Spørgsmålindgang, så clearing har vi:
Spørgsmålindgang = Arbejde / effektivitet = 1530 J / 0,22 = 6954,5 J
b) Mængden af varme, der overføres til den koldeste tank, findes fra ΔW = Qindgang - SpørgsmålAfslut
SpørgsmålAfslut = Qindgang - ΔW = 6954,5 -1530 J = 5424,5 J.
En anden måde er fra ogmaks = 1 - (Tto/ T1). Da temperaturerne ikke er kendt, men de er relateret til varme, kan effektiviteten også udtrykkes som:
ogmaks = 1 - (Qgav efter/ Qabsorberet)
Referencer
- Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 1. Mc Graw Hill. 654-657
- Atomenergi. Drift af et atomkraftværk. Gendannet fra: energia-nuclear.net
- Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1. 7. Ed. Cengage Learning. 618-622.
- Tippens, P. 2011. Fysik: begreber og applikationer. 7. udgave. MacGraw Hill. 414-416.
- Walker, J. 2008. Fysik. 4. udgave Addison Wesley. 610-630



Endnu ingen kommentarer