
Vekselstrømskredsløbstyper, applikationer, eksempler
Det vekselstrømskredsløb eller vekselstrømskredsløb består af kombinationer af resistive, induktive og kapacitive elementer kombineret med en alternerende spændingskilde, som normalt er sinusformet.
Ved at anvende spændingen etableres en variabel strøm i kort tid kaldet en forbigående strøm, der giver plads til den sinusformede stående strøm.
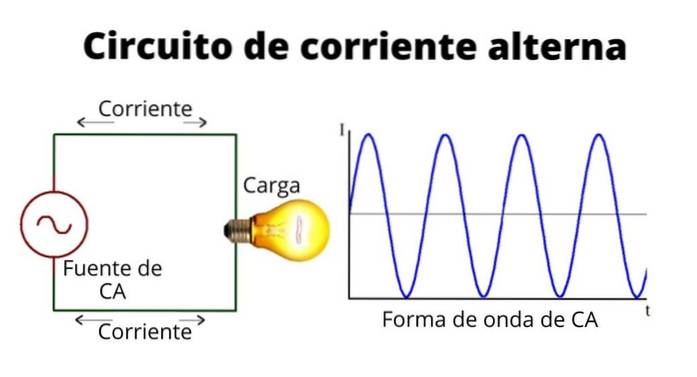
Den sinusformede strøm har værdier, der skifter mellem positiv og negativ, og ændres med regelmæssige intervaller bestemt af en tidligere etableret frekvens. Strømformen udtrykkes som:
I (t) = Im synd (ωt - φ)
Hvor jegm er den maksimale strøm eller strømamplitude, ω er frekvensen, t er tiden og φ faseforskellen. Almindeligt anvendte enheder til strøm er ampere (A) og dens submultipler, såsom milliampere og mikroampere..
For sin del måles tiden i sekunder, for frekvensen er der hertz eller Hertz, forkortet Hz, mens faseforskellen er en vinkel, der generelt måles i radianer, selvom den også undertiden er angivet i grader. Hverken disse eller radianerne betragtes som enheder.

Vekselspændingen symboliseres ofte af bølgen inde i cirklen for at skelne den fra den direkte spænding, symboliseret ved de to ulige og parallelle linjer.
Artikelindeks
- 1 Typer af vekselstrømskredsløb
- 1.1 Kredsløb med resistivt element
- 1.2 Kredsløb med induktivt element
- 1.3 Kredsløb med kapacitivt element
- 2 applikationer
- 2.1 Faseskiftende kredsløb
- 2.2 Brokredsløb
- 3 Eksempler på vekselstrømskredsløb
- 3.1 Eksempel 1: Serie RLC-kredsløb
- 3.2 Eksempel 2: RLC-kredsløb parallelt
- 4 Øvelse løst
- 4.1 Løsning a
- 4.2 Løsning b
- 4.3 Løsning c
- 5 Interessante emner
- 6 Referencer
Typer af vekselstrømskredsløb
Der er mange slags vekselstrømskredsløb, der starter med de enkleste kredsløb vist i den følgende figur. Fra venstre mod højre har du:
-Kredsløb med modstand R
-Kredsløb med spole L
-Kredsløb med kondensator C.

Kredsløb med resistivt element
I kredsløbet med en modstand R forbundet med en alternerende spændingskilde er spændingen over modstanden V.R = Vm sen ωt. Ved Ohms lov, som også er gyldig for rent resistive vekselstrømskredsløb:
VR = JegR∙ R
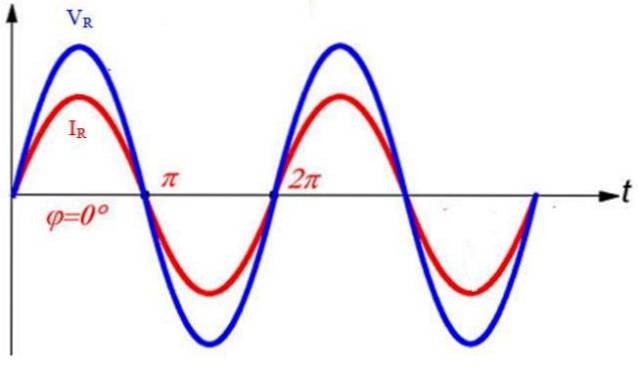
Derfor er den maksimale strøm Im = Vm / R.
Både strøm og spænding er i fase, hvilket betyder, at de når deres maksimale værdier såvel som 0 på samme tid.

Induktivt element kredsløb
I spole L er spændingen V.L = Vm sin ωt og er relateret til strømmen i induktoren ved ligningen:
Integrering:

Ved egenskaber ved trigonometriske forhold, IL er skrevet i form af synd ωt som:
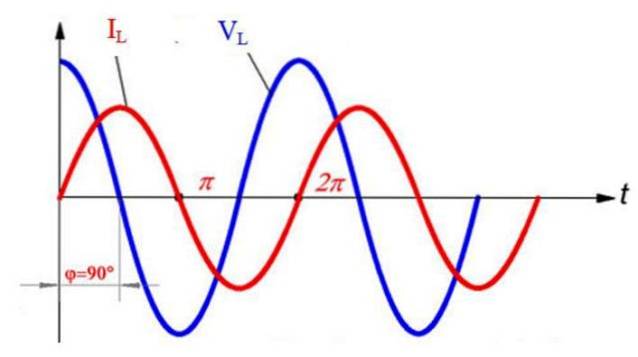
jegL = Jegm sin (ωt - ½ π)
Derefter er spændingen og strømmen ude af fase, hvor sidstnævnte halter ½ π = 90º i forhold til spændingen (strømmen starter tidligere med t = 0 s startpunktet). Dette ses i den følgende figur, der sammenligner sinusformet af IL og VL:

Induktiv reaktans
Induktiv reaktans er defineret som XL = ωL, øges med frekvens og har dimensioner af modstand, derfor analogt med Ohms lov:
VL = JegL ∙ XL
Kredsløb med kapacitivt element
For en kondensator C tilsluttet en vekselstrømskilde er det rigtigt, at:
Q = C ∙ VC = C ∙ Vm sen ωt
Strømmen i kondensatoren findes ved at flytte opladningen med hensyn til tid:
jegC= ωC ∙ Vm cos ωt
Men cos ωt = sin (ωt + ½ π), så:
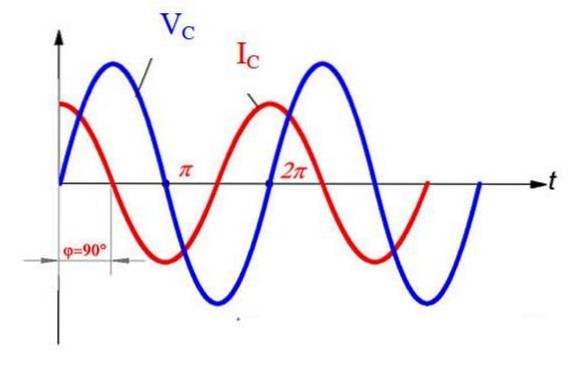
jegC = ωCVm sin (ωt + ½ π)
I dette tilfælde fører strømmen spændingen med ½ π, som det fremgår af grafen.

Kapacitiv reaktans
Kapacitiv reaktans kan skrives XC = 1 / ωC, det falder med frekvensen og har også modstandsenheder, dvs. ohm. På denne måde ser Ohms lov sådan ud:
VC = XC.jegC
Ansøgninger
Michael Faraday (1791-1867) var den første til at opnå en strøm, der med jævne mellemrum ændrede sin betydning gennem hans induktionseksperimenter, selvom der i de tidlige dage kun blev brugt jævnstrøm..
I slutningen af det 19. århundrede opstod den velkendte strøm af krig mellem Thomas A. Edison, forsvarer af brugen af jævnstrøm og George Westinghouse, tilhænger af vekselstrøm. Endelig var dette den der vandt på grund af økonomi, effektivitet og nem transmission med lavere tab..
Af denne grund er strømmen, der når hjem og industrier, til dato vekselstrøm, skønt brugen af jævnstrøm aldrig er forsvundet helt..
Vekselstrøm bruges til næsten alt, og i mange applikationer er den konstante ændring af vekselstrømsretning ikke relevant, såsom pærer, strygejernet eller komfuret til madlavning, da opvarmningen af det resistive element ikke afhænger af retning af lasternes bevægelsesretning.
I stedet er det faktum, at strømmen skifter retning med en bestemt frekvens, grundlaget for elektriske motorer og forskellige mere specifikke anvendelser, såsom følgende:
Faseskiftende kredsløb
Kredsløb, der består af en alternerende kilde, der er forbundet til en modstand og en kondensator i serie, er kendt som RC-seriekredsløb og bruges til at eliminere uønskede faseskift i et andet kredsløb eller for at tilføje en særlig effekt til det..
De fungerer også som spændingsdelere og til at indstille radiostationer (se eksempel 1 i næste afsnit).
Brokredsløb
Bridge-type kredsløb fodret med vekselstrøm kan bruges til at måle kapacitans eller induktans på samme måde som Wheatstone bridge, et kendt jævnstrømskredsløb, der er i stand til at måle værdien af en ukendt modstand..
Eksempler på vekselstrømskredsløb
I de foregående afsnit blev de enkleste vekselstrømskredsløb beskrevet, selvom de grundlæggende elementer beskrevet ovenfor, såvel som andre lidt mere komplekse, såsom dioder, forstærkere og transistorer, for at nævne nogle få, kan kombineres for at opnå forskellige effekter ..
Eksempel 1: Serie RLC-kredsløb
Et af de mest almindelige kredsløb i AC er den, der inkluderer en modstand R, en spole eller induktor L og en kondensator eller kondensator C anbragt i serie med en vekselstrømskilde.
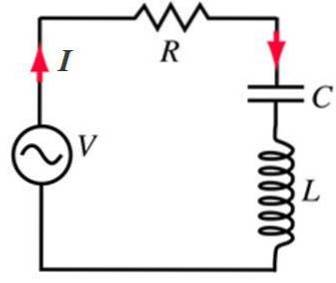
Serie RLC-kredsløb reagerer på en bestemt måde på frekvensen af den alternerende kilde, hvorfra de tilføres. Derfor er en af de mest interessante applikationer som radiotunerkredsløb..
Et radiosignal med frekvens ω genererer en strøm med den samme frekvens i et kredsløb, der er specielt designet til at tjene som modtager, og amplituden af denne strøm er maksimal, hvis modtageren er indstillet til denne frekvens gennem en effekt kaldet resonans.
Modtagerkredsløbet fungerer som en tuner, fordi det er designet, så signaler om uønskede frekvenser genererer meget små strømme, som ikke registreres af radiohøjttalerne og derfor ikke høres. I stedet når strømens amplitude ved resonansfrekvensen et maksimum, og signalet høres tydeligt..
Resonansfrekvensen opstår, når kredsløbets induktive og kapacitive reaktanser udligner:
xL = XC
1 / ωC = ωL
ωto = 1 / LC
Radiostationen med frekvenssignalet ω siges at være "tunet ind", og værdierne for L og C vælges for den pågældende frekvens..
Eksempel 2: RLC-kredsløb parallelt
Parallelle RLC-kredsløb har også visse reaktioner i henhold til kildens frekvens, hvilket afhænger af reaktansen af hvert af elementerne, defineret som forholdet mellem spænding og strøm..
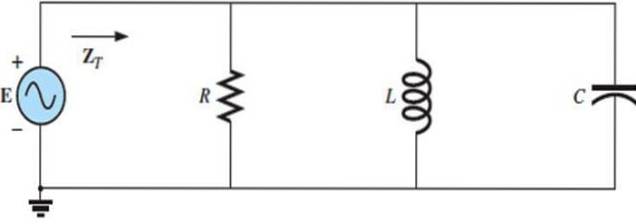
Træning løst
I serie LRC-kredsløbet i eksempel 1 i det foregående afsnit er modstanden 200 ohm, induktansen er 0,4 H, og kondensatoren er 6 μF. På sin side er strømforsyningen en alternerende spænding med amplitude svarende til 30 V med en frekvens på 250 rad / s. Det bliver bedt om at finde:
a) Reaktanserne for hvert element
b) Værdien af modulet til impedansen af kredsløbet.
c) Strømens amplitude
Løsning til
De respektive reaktanser beregnes med formlerne:
xC = 1 / ωC = 1 / (250 rad / s x 6 x 10-6 F) = 666,67 ohm
xL = ωL = 250 rad / s x 0,4 H = 100 ohm
Og modstandens reaktans er lig med dens værdi i ohm:
xR = R = 200 ohm
Løsning b
Impedans Z defineres som forholdet mellem spænding og strøm i kredsløbet, enten i serie eller parallelt:
Z = Vm / Jegm
Impedansen måles i ohm, det samme som en modstand eller en reaktans, men det henviser til modstanden mod strømmen af induktanserne og kondensatorerne, i betragtning af at ud over dens særlige virkninger, såsom forsinkelse eller fremadspænding, det har også en vis intern modstand.
Det kan vises, at for serie RLC-kredsløbet gives impedansmodulet ved:
Ved vurdering af værdierne i erklæringen opnår vi:

Løsning c
Fra:
Z = Vm / Jegm
Det skal det;
jegm = Vm / Z = 30V / 601 ohm = 0,05 A..
Temaer af interesse
Forskelle mellem vekselstrøm og jævnstrøm
Referencer
- Alexander, C. 2006. Grundlæggende om elektriske kredsløb. 3. Udgave. Mc Graw Hill.
- Boylestad, R. 2011. Introduktion til kredsløbsanalyse. 2da. Udgave. Pearson.
- Figueroa, D. (2005). Serie: Fysik til videnskab og teknik. Bind 6. elektromagnetisme. Redigeret af Douglas Figueroa (USB).
- Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14. Red. Bind 1. Pearson.
- Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1. 7. Ed. Cengage Learning.



Endnu ingen kommentarer