
Ledningsformler, beregning, eksempler, øvelser
Det ledningsevne af en leder defineres som det anlæg, den har til at passere den elektriske strøm. Det afhænger ikke kun af det anvendte materiale til dets fremstilling, men også af dets geometri: længde og tværsnitsareal.
Symbolet, der bruges til ledningsevne, er G, og det er det omvendte af elektrisk modstand R, en lidt mere velkendt størrelse. SI International System-enheden for ledningsevne er omvendt af ohm, betegnet som Ω-1 og modtager navnet på siemens (S).

Andre udtryk, der bruges i elektricitet, der ligner ledningsevne og er beslægtede, er ledningsevne og kørsel, men de skal ikke forveksles. Den første af disse termer er en iboende egenskab af det stof, som lederen er fremstillet med, og det andet beskriver strømmen af elektrisk ladning gennem den..
Til en elektrisk leder med konstant tværsnitsareal TIL, længde L og ledningsevne σ, konduktansen er givet af:
G = σ.A / L
Jo højere ledningsevne, jo højere ledningsevne. Jo større tværsnitsarealet er, jo lettere er det for lederen at passere strøm. Tværtimod, jo større længden L er, desto lavere ledningsevne, da de nuværende bærere mister mere energi på længere stier..
Artikelindeks
- 1 Hvordan beregnes konduktans?
- 1.1 Ledningsenheder
- 2 Eksempler
- 2.1 Ledningsevne og ledningsevne
- 2.2 Modstande parallelt
- 3 Øvelser
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 4 Referencer
Hvordan beregnes konduktans?
Konduktansen G for en leder med konstant tværsnitsareal beregnes i henhold til ligningen ovenfor. Dette er vigtigt, for hvis tværsnittet ikke er konstant, skal du bruge den integrerede beregning til at finde både modstanden og ledningsevnen.
Da det er det modsatte af modstanden, kan konduktansen G beregnes ved at vide, at:
G = 1 / R
Faktisk kan lederens elektriske modstand måles direkte med et multimeter, en enhed, der også måler strøm og spænding..
Ledningsenheder
Som anført i starten er ledningsenheden i det internationale system Siemens (S). En leder siges at have en ledningsevne på 1 S, hvis strømmen igennem den øges med 1 ampere for hver volt potentialforskel.
Lad os se, hvordan det er muligt gennem Ohms lov, hvis det er skrevet med hensyn til konduktans:
V = I.R = I / G
Hvor V er spændingen eller potentialforskellen mellem enderne af lederen e jeg strømintensitet. Med hensyn til disse størrelser ser formlen sådan ud:
G = I / V
Tidligere var enheden for konduktans den mho (ohm skrevet baglæns) betegnet som Ʊ, som er en omvendt kapital omega. Denne notation blev udfaset og blev erstattet af siemens til ære for den tyske ingeniør og opfinder Ernst Von Siemens (1816-1892), pioner inden for telekommunikation, men begge er helt ækvivalente.
1 mho = 1 siemen = 1 A / V (ampere / volt)
I andre målesystemer statsiemens (statS) (i cgs eller centimeter-gram-sekund-systemet) og absiemens (abS) (elektromagnetisk cgs-system) med "s" i slutningen uden at indikere ental eller flertal, da de kommer fra et eget navn.
Nogle ækvivalenser
1 statS = 1.11265 x 10 -12 siemens
1 abS = 1 x 109 siemens
Eksempler
Som nævnt før er konduktansen straks kendt, når man har modstand, når man bestemmer den inverse eller gensidige værdi. På denne måde svarer en elektrisk modstand på 100 ohm f.eks. Til 0,01 siemen.
Her er to eksempler på brugen af konduktans:
Ledningsevne og ledningsevne
De er forskellige udtryk, som allerede angivet. Ledningsevne er en egenskab af det stof, som lederen er fremstillet med, mens ledning er korrekt for lederen.
Ledningsevne kan udtrykkes i form af G som:
σ = G. (L / A)
Her er en tabel med ledningsevne for ofte anvendte ledende materialer:
tabel 1. Ledningsevne, resistivitet og termisk koefficient for nogle ledere. Referencetemperatur: 20 ºC.
| Metal | σ x 106 (I) | ρ x 10-8 (Ω.m) | α ºC-1 |
|---|---|---|---|
| Sølv | 62.9 | 1,59 | 0,0058 |
| Kobber | 56.5 | 1,77 | 0,0038 |
| Guld | 41,0 | 2.44 | 0,0034 |
| Aluminium | 35.4 | 2.82 | 0,0039 |
| Wolfram | 18.0 | 5.60 | 0,0045 |
| Jern | 10,0 | 10,0 | 0,0050 |
Modstande parallelt
Når du har kredsløb med modstande parallelt, er det undertiden nødvendigt at opnå den tilsvarende modstand. At kende værdien af den tilsvarende modstand gør det muligt at erstatte en enkelt værdi for sættet af modstande.
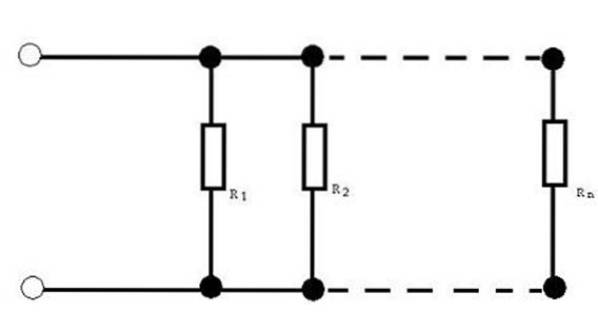
For denne modstandskonfiguration er den tilsvarende modstand givet af:
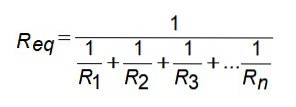
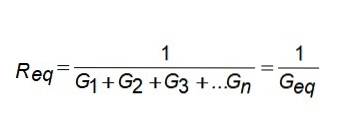
Gækv = G1 + Gto + G3 +... Gn
Det vil sige, den tilsvarende ledningsevne er summen af ledningsevnen. Hvis du vil vide den tilsvarende modstand, skal du blot vende resultatet.
Uddannelse
- Øvelse 1
a) Skriv Ohms lov med hensyn til konduktans.
b) Find ledningen af en wolframtråd, der er 5,4 cm lang og 0,15 mm i diameter.
c) Nu ledes en strøm på 1,5 A gennem ledningen. Hvad er den potentielle forskel mellem enderne af denne leder?
Løsning til
Fra de foregående afsnit skal du:
V = I / G
G = σ.A / L
Ved at erstatte sidstnævnte i det første ser det sådan ud:
V = I /(σ.A/L) = I.L / σ.A
Hvor:
-Jeg er strømens intensitet.
-L er lederens længde.
-σ er ledningsevne.
-A er tværsnitsarealet.
Løsning b
For at beregne ledningen af denne wolframtråd kræves dens ledningsevne, som findes i tabel 1:
σ = 18 x 106 Ye
L = 5,4 cm = 5,4 x 10-to m
D = 0,15 mm = 0,15 x 10-3 m
A = π.Dto / 4 = π. (0,15 x 10-3 m)to / 4 = 1,77 x 10-8 mto
Udskiftning i ligningen har vi:
G = σ.A / L = 18 x 106 Ye. 1,77 x 10-8 mto / 0,15 x 10-3 m = 2120,6 S.
Løsning c
V = I / G = 1,5 A / 2120,6 S = 0,71 mV.
- Øvelse 2
Find den ækvivalente modstand i det følgende kredsløb og vel vidende at jegeller = 2 A, beregne ix og strømmen spredt af kredsløbet:
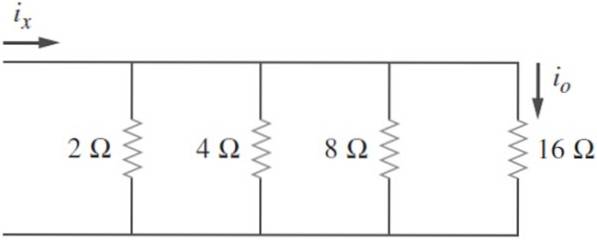
Opløsning
Modstande er anført: R1= 2 Ω; Rto= 4 Ω; R3= 8 Ω; R4= 16 Ω
Derefter beregnes konduktansen i hvert tilfælde: G1 = 0,5 Ʊ; Gto = 0,25 Ʊ; G3 = 0,125 Ʊ; G4 = 0,0625 Ʊ
Og til sidst tilføjes de som angivet før for at finde den tilsvarende ledningsevne:
Gækv = G1 + Gto + G3 +... Gn = 0,5 Ʊ + 0,25 Ʊ + 0,125 Ʊ + 0,0625 Ʊ = 0,9375 Ʊ
Derfor Rækv = 1,07 Ω.
Spændingen over R4 er V4 = ieller. R4 = 2 A. 16 Ω = 32 V, og det er det samme for alle modstande, da de er forbundet parallelt. Så er det muligt at finde de strømme, der strømmer gennem hver modstand:
-jeg1 = V1 / R1 = 32 V / 2 Ω = 16 A.
-jegto = Vto / Rto = 32 V / 4 Ω = 8 A.
-jeg3 = V3 / R3 = 32 V / 8 Ω = 4 A.
-jegx = i1 + jegto + jeg3 + jegeller = 16 + 8 + 4 + 2 A = 30 A.
Endelig er den spredte kraft P:
P = (ix)to. Rækv = 30 A x 1,07 Ω = 32,1 W
Referencer
- Alexander, C. 2006. Grundlæggende om elektriske kredsløb. 3. Udgave. Mcgraw bakke.
- Konvertering megaampere / millivolt til absiemens lommeregner. Gendannet fra: pinkbird.org.
- García, L. 2014. Elektromagnetisme. 2. plads Udgave. Industrial University of Santander. Colombia.
- Knight, R. 2017. Fysik for forskere og teknik: en strategi tilgang. Pearson.
- Roller, D. 1990. Fysik. Elektricitet, magnetisme og optik. Bind II. Redaktionel Reverté.
- Wikipedia. Elektrisk ledning. Gendannet fra: es.wikipedia.org.
- Wikipedia. Siemens. Gendannet fra: es.wikipedia.org.


Endnu ingen kommentarer