
Kongruens kongruente figurer, kriterier, eksempler, øvelser
Det overensstemmelsen, I geometri påpeger det, at hvis to plane figurer har samme form og dimensioner, er de kongruente. For eksempel er to segmenter kongruente, når deres længder er ens. Ligeledes har kongruente vinkler samme mål, selvom de ikke er orienteret på samme måde i planet..
Udtrykket "kongruens" kommer fra latin kongruent, hvis betydning er korrespondance. Således svarer to kongruente figurer nøjagtigt til hinanden..
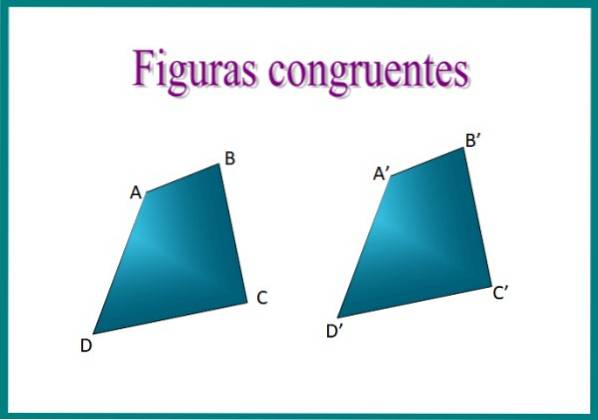
For eksempel, hvis vi overlejrer de to firkanter i billedet, vil vi finde ud af, at de er kongruente, da arrangementet af deres sider er identisk, og de måler det samme.
Ved at placere firkanter ABCD og A'B'C'D 'oven på hinanden, vil tallene matche nøjagtigt. De matchende sider kaldes homologe sider eller tilsvarende og for at udtrykke kongruens bruges symbolet ≡. Så kan vi sige, at ABCD ≡ A'B'C'D '.
Artikelindeks
- 1 Congruence kriterier
- 1.1 Kongruens, identitet og lighed
- 2 Eksempler på kongruens
- 2.1 - Vinkelkongruens
- 2.2 - Kongres af trekanter
- 3 Løst øvelser
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 4 Referencer
Kongruensskriterier
Følgende egenskaber er fælles for kongruente polygoner:
-Samme form og størrelse.
-Identiske mål for deres vinkler.
-Det samme mål på hver af dets sider.
I tilfælde af at de to polygoner er regelmæssige, dvs. at alle sider og interne vinkler måler det samme, er kongruens sikret, når den er opfyldt nogle af følgende betingelser:
-Siderne er kongruente
-Det apoteker de har samme mål
-Det radio af hver polygon måler lige
Apotemet til en regelmæssig polygon er afstanden mellem centrum og en af siderne, mens radius svarer til afstanden mellem centrum og et hjørne af figuren.
Kongruenskriterier bruges ofte, fordi så mange dele og stykker af alle slags masseproduceres og skal have samme form og målinger. På denne måde kan de let udskiftes, når det er nødvendigt, for eksempel møtrikker, bolte, plader eller belægningsstenene på jorden på gaden..

Kongruens, identitet og lighed
Der er f.eks. Geometriske begreber relateret til kongruens identiske tal og lignende tal, der ikke nødvendigvis indebærer, at tallene er kongruente.
Bemærk, at de kongruente figurer er identiske, men firkanterne i figur 1 kunne orienteres på forskellige måder på planet og stadig forblive kongruente, da den forskellige orientering ikke ændrer størrelsen på deres sider eller deres vinkler. I dette tilfælde ophører de med at være identiske.
Det andet koncept er, at der er lighed mellem figurer: to plane figurer er ens, hvis de har samme form, og deres indre vinkler måler den samme, selvom størrelsen på figurerne kan være forskellig. Hvis dette er tilfældet, er tallene ikke kongruente.
Eksempler på kongruens
- Vinkelkongruens
Som vi angav i starten, har kongruente vinkler det samme mål. Der er flere måder at opnå kongruente vinkler på:
Eksempel 1
To linjer med et fælles punkt definerer to vinkler, kaldet Modsatte vinkler ved toppunktet. Disse vinkler har samme mål, derfor er de kongruente.
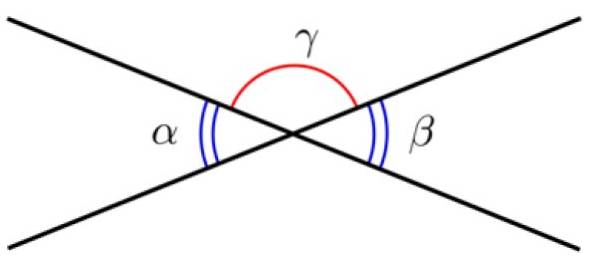
Eksempel 2
Der er to parallelle linjer plus en linje t der skærer dem begge. Som i det foregående eksempel, når denne linje skærer parallellerne, genererer den kongruente vinkler, en på hver linje på højre side og en anden to på venstre side. Figuren viser α og α1, til højre for linjen t, der er kongruente.
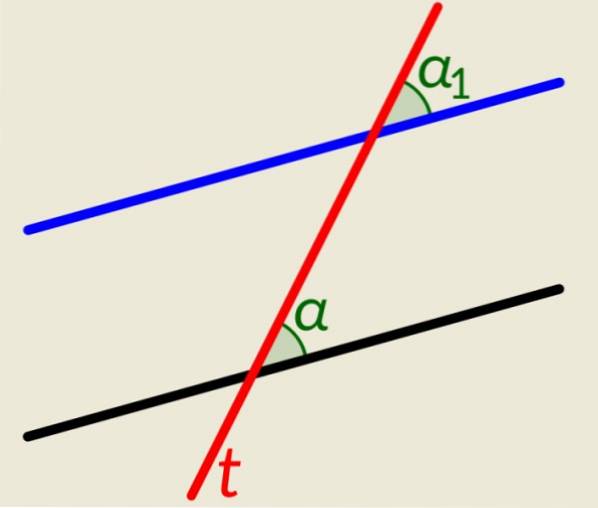
Eksempel 3
I et parallelogram er der fire indvendige vinkler, som er kongruente to til to. Det er dem, der er mellem modstående hjørner, som vist i den følgende figur, hvor de to vinkler i grønt er kongruente, såvel som de to vinkler i rødt.
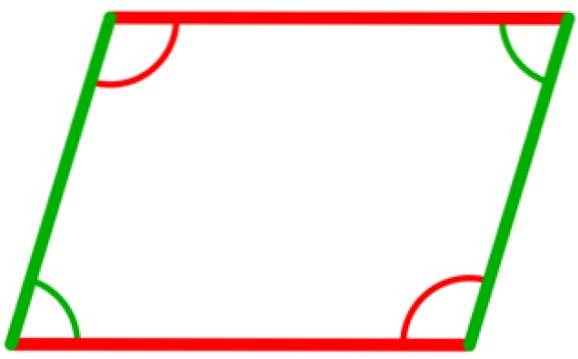
- Kongruens af trekanter
To trekanter af samme form og størrelse er kongruente. For at kontrollere dette er der tre kriterier, der kan undersøges på jagt efter kongruens:
-Kriterium LLL: de tre sider af trekanterne har de samme mål, derfor L1 = L '1; Lto = L 'to og L3 = L '3.
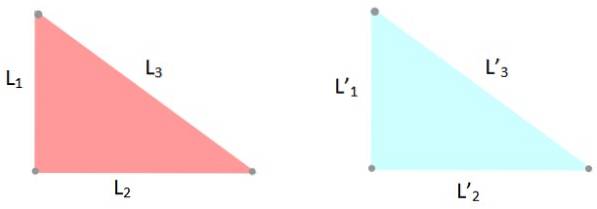
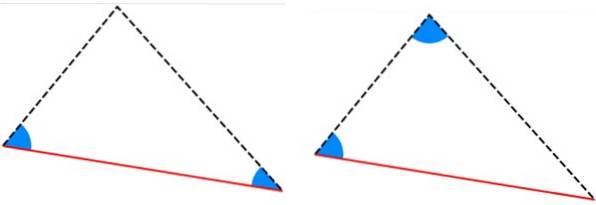
-ALA og AAL kriterier: trekanter har to lige indvendige vinkler, og siden mellem disse vinkler har samme mål.
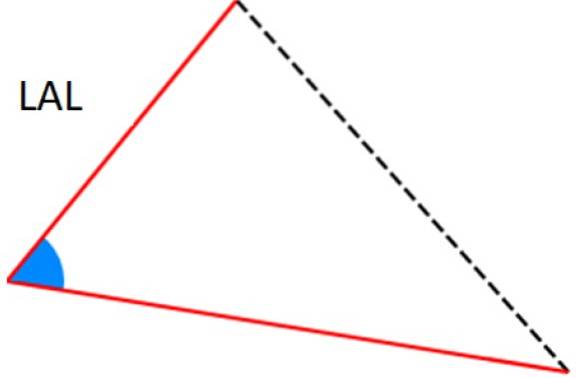
-LAL-kriterium: to af siderne er identiske (svarende) og mellem dem er der den samme vinkel.
Løst øvelser
- Øvelse 1
To trekanter er vist i følgende figur: ΔABC og ΔECF. Det vides, at AC = EF, at AB = 6 og at CF = 10. Desuden er vinklerne ∡BAC og ∡FEC kongruente, og vinklerne ∡ACB og ∡FCB er også kongruente..
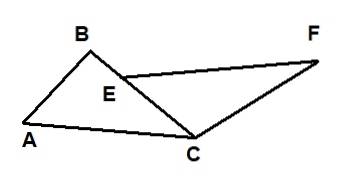
Derefter er længden af segment BE lig med:
(i) 5
(ii) 3
(iii) 4
(iv) 2
(v) 6
Opløsning
Da de to trekanter har en side med lige længde AC = EF, der er mellem de samme vinkler ∡BAC = ∡CEF og ∡BCA = ∡CFE, kan det siges, at de to trekanter er kongruente efter ALA-kriteriet.
Det vil sige ΔBAC ≡ ΔCEF, så vi skal:
BA = CE = AB = 6
BC = CF = 10
AC = EF
Men det segment, der skal beregnes, er BE = BC - EC = 10 - 6 = 4.
Så det rigtige svar er (iii).
- Øvelse 2
Tre trekanter er vist i nedenstående figur. Det er også kendt, at de to angivne vinkler måler 80 ° hver, og at segmenterne AB = PD og AP = CD. Find værdien af vinklen X angivet i figuren.
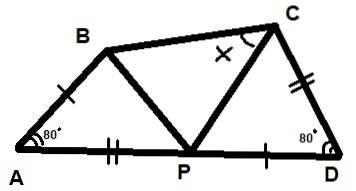
Opløsning
Du skal anvende egenskaberne for trekanterne, som er detaljerede trin for trin.
Trin 1
Startende med LAL-trekongruenskriteriet kan det siges, at BAP- og PDC-trekanterne er kongruente:
ΔBAP ≡ ΔPDC
Trin 2
Ovenstående fører til at bekræfte, at BP = PC, derfor er trekanten ΔBPC ligebenede og ∡PCB = ∡PBC = X.
Trin 3
Hvis vi kalder vinklen BPC γ, følger det at:
2x + γ = 180º
Trin 4
Og hvis vi kalder vinklerne APB og DCP β og α vinklerne ABP og DPC, har vi:
α + β + γ = 180º (da APB er en plan vinkel).
Trin 5
Desuden er α + β + 80º = 180º ved summen af de indre vinkler i trekanten APB.
Trin 6
Ved at kombinere alle disse udtryk har vi:
α + β = 100º
Trin 7
Og derfor:
γ = 80º.
Trin 8
Endelig følger det, at:
2X + 80º = 180º
Med X = 50º.
Referencer
- Baldor, A. 1973. Plane and Space Geometry. Centralamerikansk kultur.
- CK-12 Foundation. Kongruente polygoner. Gendannet fra: ck 12.org.
- Nyd matematik. Definitioner: Radius (polygon). Gendannet fra: gustolasmatematicas.com.
- Math Open Reference. Test af polygoner for kongruens. Gendannet fra: mathopenref.com.
- Wikipedia. Kongruens (geometri). Gendannet fra: es.wikipedia.org.
- Zapata, F. Trekanter, historie, elementer, klassifikation, egenskaber. Gendannet fra: lifeder.com.



Endnu ingen kommentarer