Det forstås af endeligt sæt ethvert sæt med et begrænset eller tælleligt antal elementer. Eksempler på begrænsede sæt er kuglerne, der er indeholdt i en pose, sæt huse i et kvarter eller sættet P dannet af de første tyve (20) naturlige tal:
P = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
Sættet af stjerner i universet er helt sikkert enormt, men det vides ikke med sikkerhed, om det er endeligt eller uendeligt. Sættet af planeter i solsystemet er dog endeligt.
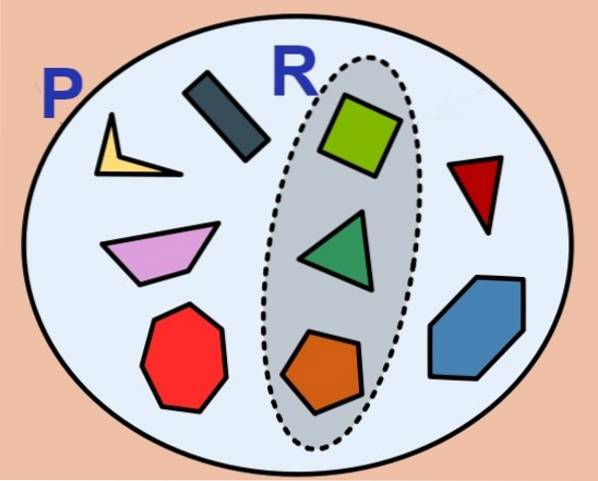
Antallet af elementer i et endeligt sæt kaldes dets kardinalitet og for sættet P betegnes således: Kort (P) eller #P. Det tomme sæt har nul kardinalitet og betragtes som et endeligt sæt.
Artikelindeks
Blandt egenskaberne ved begrænsede sæt er følgende:
1- Foreningen af endelige sæt giver anledning til et nyt endeligt sæt.
2- Hvis to endelige sæt krydser hinanden, resulterer et nyt endeligt sæt.
3- Et undersæt af et begrænset sæt er endeligt, og dets kardinalitet er mindre end eller lig med det originale sæt.
4- Det tomme sæt er et endeligt sæt.
Der er mange eksempler på begrænsede sæt. Nogle eksempler inkluderer følgende:
Sæt M af årets måneder, som i udvidet form kan skrives således:
M = Januar, februar, marts, april, maj, juni, juli, august, september, oktober, november, december, kardinaliteten i M er 12.
Sæt S af ugedagene: S = Mandag, tirsdag, onsdag, torsdag, fredag, lørdag, søndag. Kardinaliteten af S er 7.
Sæt Ñ af bogstaverne i det spanske alfabet er et endeligt sæt, dette sæt ved forlængelse er skrevet således:
Ñ = a, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, x, y, z og dens kardinalitet er 27.
Sæt V af vokalerne på spansk er en delmængde af sættet Ñ:
V ⊂ Ñ derfor er det et endeligt sæt.
Det endelige sæt V i omfattende form er det skrevet således: V = a, e, i, o, u og dens kardinalitet er 5.
Sæt kan udtrykkes ved forståelse. Sæt F sammensat af bogstaverne i ordet "endelig" er et eksempel:
F = x / x er et bogstav i ordet "finite"
Nævnte sæt udtrykt på en omfattende måde vil være:
F = f, i, n, t, o hvis kardinalitet er 5 og derfor er et endeligt sæt.
Regnbuens farver er et andet eksempel på et endeligt sæt, sættet C af disse farver er:
C = rød, orange, gul, grøn, cyan, blå, violet og dens kardinalitet er 7.
Sættet af faser F de la Luna er et andet eksempel på et begrænset sæt:
F = Nymåne, første kvartal, fuldmåne, sidste kvartal dette sæt har kardinalitet 4.
Et andet endeligt sæt er det, der dannes af solsystemets planeter:
P = Kviksølv, Venus, Jorden, Mars, Jupiter, Saturn, Uranus, Neptun, Pluto af kardinalitet 9.
Følgende sæt A = x∊ R / x ^ 3 = 27 er givet. Udtryk det med ord og skriv det i forlængelse, angiv dets kardinalitet og sig, om det er endeligt eller ej.
Opløsning: Sæt A er sættet med reelle tal x, således at x kuberes som et resultat 27.
Ligningen x ^ 3 = 27 har tre løsninger: de er x1 = 3, x2 = (-3/2 + 3√3 / 2 i) og x3 = (-3/2 - 3√3 / 2 i). Af de tre løsninger er kun x1 reel, mens de to andre er komplekse tal.
Da definitionen af sættet A siger, at x hører til de reelle tal, er løsningerne i de komplekse tal ikke en del af sættet A.
Sættet A udtrykt udførligt er:
A = 3, som er et endeligt sæt kardinalitet 1.
Skriv i symbolsk form (ved forståelse) og i omfattende form sæt B af reelle tal, der er større end 0 (nul) og mindre end eller lig med 0 (nul). Angiv dets kardinalitet, og om det er endeligt eller ej.
Opløsning: B = x∊ R / 0 < x <= 0
Sættet B er tomt, fordi et reelt tal x ikke kan være større og mindre end nul samtidigt, ligesom det ikke kan være 0 og også mindre end 0.
B = og dens kardinalitet er 0. Det tomme sæt er et endeligt sæt.
Sættet S for løsningerne i en bestemt ligning er givet. Sættet S ved forståelse er skrevet således:
S = x∊ R / (x-3) (x ^ 2 - 9x + 20) = 0
Skriv nævnte sæt i omfattende form, angiv dets kardinalitet, og angiv, om det er et endeligt sæt.
Opløsning: For det første opnås det, når man analyserer udtrykket, der beskriver sættet S, at det er et sæt reelle x-værdier, der er løsninger på ligningen:
(x-3) (x ^ 2 - 9x + 20) = 0 (*)
En løsning af denne ligning er x = 3, hvilket er et reelt tal og derfor tilhører S. Men der er flere løsninger, der kan opnås ved at lede efter løsningerne i den kvadratiske ligning:
(x ^ 2 - 9x + 20) = 0
Ovenstående udtryk kan beregnes som følger:
(x - 4) (x - 5) = 0
Hvilket fører os til yderligere to løsninger af den oprindelige ligning (*), som er x = 4 og x = 5. Kort sagt har ligningen (*) som løsninger 3, 4 og 5.
Sættet S udtrykt i omfattende form ser sådan ud:
S = 3, 4, 5, som har kardinalitet 3 og derfor er et endeligt sæt.
Der er to sæt A = 1, 5, 7, 9, 11 og B = x ∊ N / x er lige ^ x < 10 .
Skriv eksplicit sæt B og find unionen med sæt A. Find også skæringspunktet for disse to sæt og konkluder.
Opløsning: sæt B består af naturlige tal, således at de er lige og også er mindre end værdien 10, derfor er det i sæt B i omfattende form skrevet som følger:
B = 2, 4, 6, 8
Foreningen af sæt A med sæt B er:
A U B = 1, 2, 4, 5, 6, 7, 8, 9, 11
og skæringspunktet for sæt A med sæt B er skrevet således:
A ⋂ B = = Ø er det tomme sæt.
Det skal bemærkes, at forening og aflytning af disse to endelige sæt fører til nye sæt, som igen også er endelige.
Endnu ingen kommentarer