
Antoines konstanter formler, ligninger, eksempler
Det Antoines konstanter er tre parametre, der vises i et empirisk forhold mellem mætningsdamptryk og temperatur for rene stoffer. De afhænger af hvert stof og antages at være konstante inden for et bestemt temperaturområde.
Uden for dette interval ændrer Antoines konstanter deres værdi. Konstanterne er beslægtet med en ligning oprettet i 1888 af den franske ingeniør Louis Charles Antoine (1825-1897).
Artikelindeks
- 1 Formler og ligninger
- 2 Mætningsdamp
- 3 Hvordan beregnes Antoines konstanter??
- 4 eksempler
- 4.1 Eksempel 1
- 4.2 Eksempel 2
- 4.3 Løsning
- 5 Referencer
Formler og ligninger
Den mest almindelige måde at udtrykke Antoine-funktionen på er:
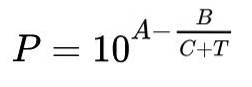
I denne formel repræsenterer P mætningsdamptrykket udtrykt i millimeter kviksølv (mmHg), T er temperaturen, der har været den uafhængige variabel og udtrykkes i ℃.
A, B og C er konstanterne eller parametrene for Antoines formel.
Betydningen af denne formel, som til trods for at den er empirisk, giver et simpelt analytisk udtryk, der let kan bruges i termodynamiske beregninger..
Antoines formel er ikke unik, der er mere præcise udtryk, der er udvidelser af denne formel, men med den ulempe, at de har seks eller flere parametre, og at deres matematiske udtryk er mere kompleks, hvilket gør dem upraktiske at bruge i termodynamiske beregninger..
Mætningsdamp
Da Antoines formel måler mætningsdamptrykket, er det nødvendigt at forklare, hvad det består af.
En væske anbringes i en glasampul eller en anden beholder. Al luft fjernes fra blisteren. Samlingen anbringes i et termisk bad, indtil ligevægt er nået..
I starten er alt flydende, men fordi der er et vakuum, begynder de hurtigere molekyler at efterlade væsken og danne en gas af det samme stof som væsken..
Ovenstående proces er fordampning og når det sker, øges damptrykket.
Nogle af dampmolekylerne mister energi og slutter sig til stoffets flydende fase igen. Dette er processen med kondensation.
Derefter optræder to processer samtidigt, fordampning og kondens. Når et lige antal molekyler kommer ud af væsken, som de er inkorporeret i, a dynamisk balance og i dette øjeblik forekommer det maksimale damptryk kendt som mætningstryk.
Det er dette dampmætningstryk, som Antoines formel forudsiger for hvert stof og hver temperatur..
I nogle faste stoffer forekommer et lignende fænomen, når man går direkte fra den faste fase til den gasformige fase uden at gå gennem væskefasen, i disse tilfælde kan et mætningsdamptryk også måles.
Det er ikke let at etablere en teoretisk model med udgangspunkt i de første principper, da ændringer i molekylær kinetisk energi er involveret, som kan være translationel, roterende og vibrerende med den indre energi af molekylær binding. Det er af denne grund, at der i praksis anvendes empiriske formler.
Hvordan beregnes Antoines konstanter??
Der er ingen teoretisk metode til at opnå Antoines konstanter, da det er et empirisk forhold.
De opnås ud fra de eksperimentelle data for hvert stof og justerer de tre parametre A, B og C, så de minimerer den kvadratiske forskel (metoden med mindst kvadrat) af forudsigelsen med de eksperimentelle data..
For slutbrugeren, som generelt er kemiske ingeniører, er der tabeller i kemihåndbøgerne, hvor disse konstanter er angivet for hvert stof, der angiver de maksimale og minimale temperaturområder, hvor de er anvendelige..
Der er også tilgængelige onlinetjenester, der giver værdierne for konstanterne A, B og C, som det er tilfældet med DDBST GmbH Onlines Services.
Der kan være mere end et gyldigt temperaturområde for det samme stof. Afhængigt af arbejdsområdet vælges derefter en eller anden gruppe konstanter.
Der kan opstå vanskeligheder, hvis arbejdsområdet for temperaturer er mellem to gyldighedsområder for konstanterne, fordi trykforudsigelserne med formlen ikke falder sammen i grænsezonen.
Eksempler
Eksempel 1
Find vandets damptryk ved 25 ℃.
Opløsning
Vi konsulterer tabellerne for at bestemme konstanterne for Antoine.
Der er to områder for vand:
Mellem 1 ℃ og 100 ℃ og mellem 99 ℃ op til 374 ℃.
Da vi er interesseret i 25 take, tager vi det første interval, hvor værdien af Antoines konstanter er:
A = 8,07131
B = 1730,63
C = 233,426
P = 10 ^ (8.07131 - 1730.63 / (25 + 233.426))
Beregning af eksponenten
Lad os først beregne eksponenten: 1.374499
P = 10 ^ 1,374499 = 23,686 mmHg = 0,031166 atm
Resultater analyse
Disse resultater fortolkes således:
Antag, at rent vand placeres i en lufttæt beholder, hvorfra luften er fjernet ved hjælp af en vakuumpumpe..
Beholderen med vandet placeres i et termisk bad ved en temperatur på 25 ℃, indtil det når termisk ligevægt..
Vandet i den hermetiske beholder fordamper delvis, indtil det når mætningsdamptrykket, hvilket ikke er andet end det tryk, hvorved den dynamiske ligevægt mellem vandets flydende fase og dampfasen etableres..
Dette tryk viste sig i dette tilfælde at være 0,031166 atm ved 25 ℃.
Eksempel 2
Find dampens tryk på vand ved 100 ℃.
Opløsning
Vi konsulterer tabellerne for at bestemme Antoines konstanter. Der er to områder for vand:
Mellem 1 ℃ og 100 ℃ og mellem 99 ℃ op til 374 ℃.
I dette tilfælde er temperaturen af interesse i de to områder.
Vi bruger det første af intervallerne [1 ℃, 100 ℃]
A = 8,07131
B = 1730,63
C = 233,426
P = 10 ^ (8.07131 - 1730.63 / (100 + 233.426))
Beregning af eksponenten
Lad os først beregne eksponenten: 2.8808
P = 10 ^ 1,374499 = 760,09 mmHg = 1.0001 atm
Dernæst bruger vi det andet af intervallerne [99 ℃, 374 ℃]
I dette tilfælde er konstanterne det
A = 8.14019
B = 1810,94
C = 244,485
P = 10 ^ (8.14019 - 1810.94 / (100 + 244.485))
Lad os først beregne eksponenten: 2.88324
P = 10 ^ 2.88324 = 764.2602 mmHg = 1.0056 atm
Der er en procentvis forskel mellem de to resultater på 0,55%.
Referencer
- Anvendelse af Raoult og Daltons love og Antoines ligning. Gendannet fra: misapuntesyantación.wordpress.com
- Antoines formel online regnemaskine. Gendannet fra: ddbonline.ddbst.de/AntoineCalculation/AntoineCalculationCGI.exe
- Gecousb. Termodynamik og dampborde / Antoines konstanter. Gendannet fra: gecousb.com.ve
- Materialets termiske egenskaber. Gendannet fra: webserver.dmt.upm.es
- Yaws og Yang. Antoine-konstante tabeller for over 700 organiske forbindelser. Gendannet fra: user.eng.umd.edu
- Wikipedia. Antoines ligning. Gendannet fra wikipedia.com
- Wikipedia. Clausius-Clapeyron ligning. Gendannet fra wikipedia.com
- Wisniak J. Historisk udvikling af damptryksligningen fra dalton til antoine. Gendannet fra: link.springer.com



Endnu ingen kommentarer