
Enhedscirkel trigonometriske funktioner og applikationer
Det enhed cirkel er en cirkel med en radius lig med 1, som normalt er centreret ved punktet (0,0) i det kartesiske koordinatsystem xy. Bruges til let at definere de trigonometriske forhold mellem vinkler ved hjælp af højre trekanter.
Ligningen for enhedens cirkel centreret ved oprindelsen er:
xto + Yto = 1
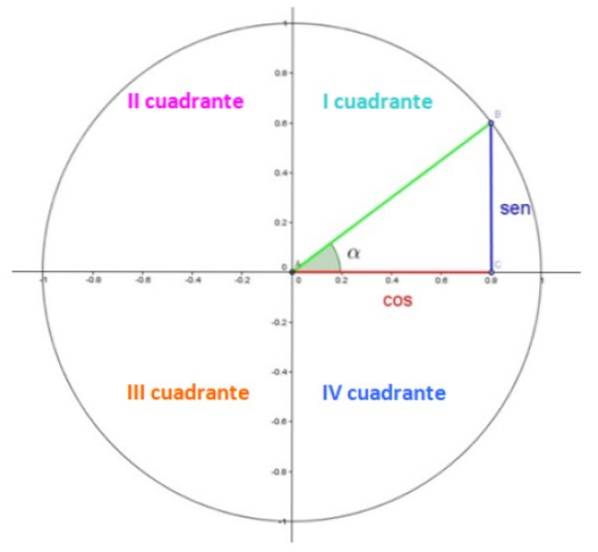
I figur 1 har vi enhedscirklen, hvor hvert kvartal er i en kvadrant. Kvadranter er nummereret med romertal og tælles mod uret.
I den første kvadrant er der en trekant. Benene, i rødt og blåt, måler henholdsvis 0,8 og 0,6, mens hypotenusen i grønt måler 1, da det er en radius.
Den spidse vinkel α er en central vinkel i standardposition, hvilket betyder, at dens toppunkt falder sammen med punktet (0,0) og dets indledende side med den positive x-akse. Vinklen måles mod uret og tildeles et positivt tegn ved konvention.
Nå, i enhedscirklen er cosinus- og sinuskoordinaterne for α henholdsvis x- og y-koordinaterne for punkt B, som i det viste eksempel er 0,8 og 0,6.
Fra disse to defineres de:
- tg α = sin α / cos α = 0,6 / 0,8 = 0,75
- sek α = 1 / cos α = 1 / 0,8 = 1,25
- cosec α = 1 / sin α = 1 / 0.6 = 1.66…
- ctg α = 1 / tg = 0,8 / 0,6 = 1,33…
Artikelindeks
- 1 Enhed cirkel applikationer
- 1.1 Referencevinkel
- 2 Tegning af graferne over cosinus og sinus
- 2.1 Egenskaber for sinus- og cosinusfunktioner
- 3 Løst øvelser
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 4 Referencer
Enhed cirkel applikationer
Hvis vi begrænser os til rigtige trekanter, gælder de trigonometriske forhold kun for akutte vinkler. Men ved hjælp af enhedscirklen udvides beregningen af de trigonometriske forhold til enhver vinkel α.
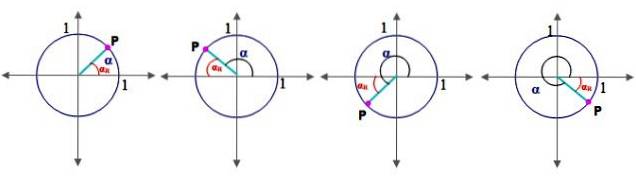
Til dette er det nødvendigt først at definere begrebet referencevinkel αR:
Referencevinkel
Lad α være en vinkel i standardposition (den hvis startside falder sammen med den positive x-akse), dens referencevinkel αR er mellem hans terminal side og x-aksen. Figur 2 viser referencevinklen for vinkler i I, II, III og IV kvadrant.
For hver kvadrant beregnes referencevinklen således:
-Første kvadrant: αR = α
-Anden kvadrant: αR = 180º - α
-Tredje kvadrant: αR = α - 180º
-Fjerde kvadrant: αR = 360º - α
Bemærk, at den første kvadrant vinklen α falder sammen med dens referencevinkel. Nå, de trigonometriske forhold for vinklen α er de samme som deres referencevinkel med tegnene i overensstemmelse med kvadranterne, hvor den endelige side af α falder..
Med andre ord falder vinklen α's trigonometriske cosinus- og sinusforhold sammen med koordinaterne for punktet P ifølge figur 2.
I den følgende figur ser vi de trigonometriske forhold mellem nogle bemærkelsesværdige vinkler, som er udledt fra enhedens cirkel.
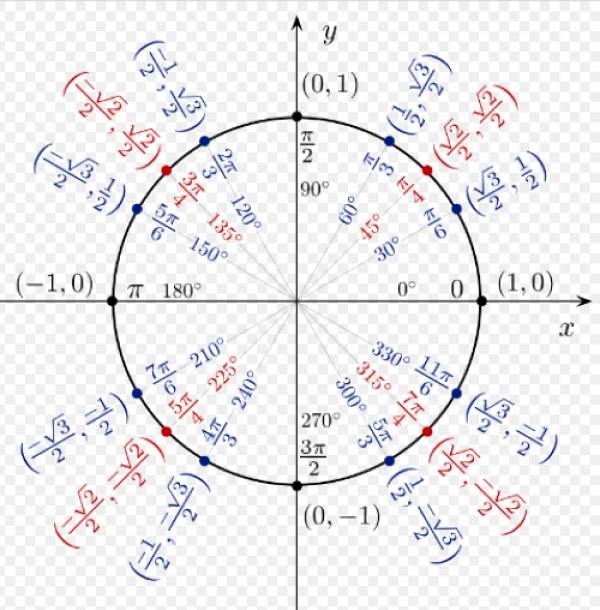
Forholdet mellem cosinus og sinus for enhver vinkel i I-kvadranten er alle positive. For α = 60º har vi koordinaterne (1/2; √3 / 2), der svarer til henholdsvis cos 60º og sin 60º.
Koordinaterne for α = 120º er (-1/2; √3 / 2), da de er i den anden kvadrant, er x-koordinaten negativ.
Tegning af cosinus- og sinusgrafer
Ved hjælp af enhedscirklen og koordinaterne for punkterne P på den er det muligt at tegne graferne for funktionerne cos t og sin t, som vi vil se nedenfor.
For at gøre dette er forskellige positioner af punktet P (t) placeret på enhedens cirkel. Vi starter med grafen for funktionen f (t) = sin t.
Vi kan se, at når vi går fra t = 0 til t = π / 2 (90º), øges værdien af sin t, indtil den når 1, hvilket er den maksimale værdi.
På den anden side falder værdien af sin t fra 1 fra t = π / 2 til t = 3π / 2 og passerer gennem 0 ved t = π indtil den når sit minimum på -1 ved t = 3π / 2.
Figuren viser grafen for den første cyklus af f (t) = sin t, der svarer til den første runde af enhedscirklen, denne funktion er periodisk med periode 2π.
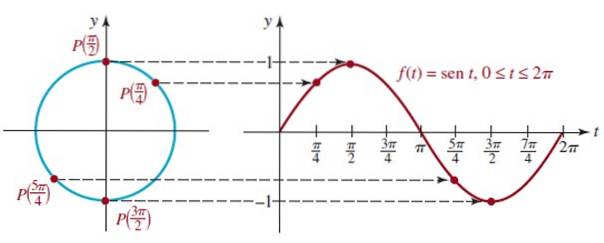
En analog procedure kan udføres for at opnå grafen for funktionen f (t) = cos t, som vist i følgende animation:
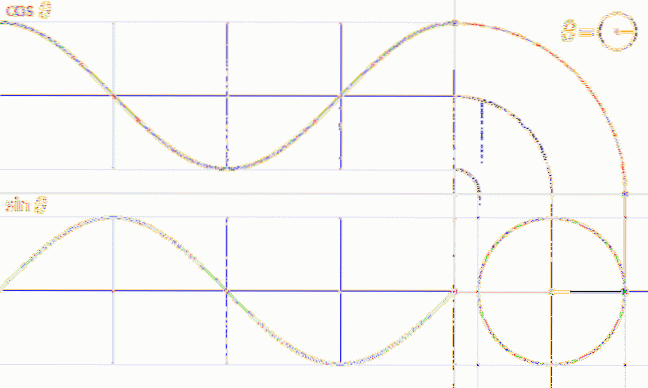
Egenskaber for sinus- og cosinusfunktioner
-Begge funktioner er kontinuerlige i sættet med reelle tal og også periodiske af periode 2π.
-Funktionernes domæne f (t) = sin t og f (t) = cos t er alle reelle tal: (-∞, ∞).
-For området eller stien til sinus og cosinus har vi intervallet [-1,1]. Parenteserne angiver, at -1 og 1 er inkluderet.
- Nullerne af sin t er de værdier, der svarer til nπ med n heltal, mens nulderne for cos t er [(2n + 1) / 2] med n også heltal.
-Funktionen f (t) = sin t er ulige, den har symmetri omkring oprindelsen, mens funktionen cos t er jævn, dens symmetri er omkring den lodrette akse.
Løst øvelser
- Øvelse 1
Givet cos t = - 2/5, som er den vandrette koordinat for punktet P (t) på enhedscirklen i den anden kvadrant, opnå den tilsvarende lodrette koordinat sin t.
Opløsning
Da P (t) hører til enhedens cirkel, hvor det er sandt, at:
xto + Yto = 1
Derfor:
y = ± √ 1 - xto
Da P (t) er i anden kvadrant, tages den positive værdi. Den lodrette koordinat for punkt P (t) er y:
y = √ 1 - (-2/5)to = √0,84
- Øvelse 2
En matematisk model for temperatur T i grader Fahrenheit på en given dag, t timer efter midnat er det givet af:
T (t) = 50 + 10 sin [(π / 12) × (t - 8)]
Med t mellem 0 og 24 timer. Finde:
a) Temperaturen kl. 8 om morgenen.
b) Timer, hvorunder T (t) = 60ºF
c) Maksimum- og minimumstemperaturer.
Løsning til
Vi erstatter t = 8 i den givne funktion:
T (8) = 50 + 10 sin [(π / 12) × (t-8)] = 50 + 10 sin [(π / 12) × (8-8)] =
= 50 + 10 x sin 0 = 50 ºF
Løsning b
50 + 10 sin [(π / 12) × (t-8)] = 60
Det er en trigonometrisk ligning, og vi skal løse det ukendte "t":
10 sin [(π / 12) × (t-8)] = 60 - 50 = 10
sin [(π / 12) × (t-8)] = 1
Vi ved, at sin π / 2 = 1, derfor skal sinusargumentet være 1:
(π / 12) × (t-8) = π / 2
t-8 = 6
t = 14 timer
Det konkluderes, at temperaturen er 14 ° efter 14 timer efter midnat, dvs. 14:00. Der er ikke noget andet tidspunkt hele dagen (24 timer), når dette sker.
Løsning c
Den maksimale temperatur svarer til den værdi, hvor sin [(π / 12) × (t-8)] = 1 og er 60 ºF. På den anden side forekommer minimumet, hvis sin [(π / 12) × (t-8)] = -1 og er 40ºF.
Referencer
- Figuera, J. 1999. Matematik. 1. Diversificeret. Bolivarian Collegiate Editions.
- Hoffman, J. Selection of Mathematics Topics. Bind 4.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Matematik er sjov. Enhedscirkel. Gendannet fra: de: mathsisfun.com.
- Wikipedia. Trigonometri identiteter og formler. Gendannet fra: es.wikipedia.org.
- Zill, D. 1984. Algebra og trigonometri. Mcgraw bakke.


Endnu ingen kommentarer