Hvad er delerne på 30?

Det kan hurtigt være kendt hvad er delerne på 30, såvel som ethvert andet tal (andet end nul), men den grundlæggende idé er at lære, hvordan delerne af et tal beregnes på en generel måde.

Der skal udvises forsigtighed, når man taler om delere, fordi det hurtigt kan fastslås, at alle delere på 30 er 1, 2, 3, 5, 6, 10, 15 og 30, men hvad med de negative af disse tal? Er de skillevægge eller ej?

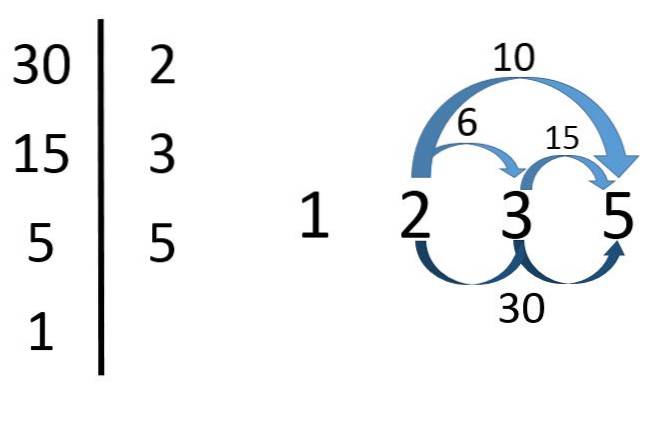
For at besvare det forrige spørgsmål er det nødvendigt at forstå et meget vigtigt udtryk i matematikens verden: divisionsalgoritmen.

Opdelingsalgoritme

Opdelingsalgoritmen (eller euklidisk opdeling) siger følgende: givet to heltal "n" og "b", hvor "b" er forskellig fra nul (b ≠ 0), er der kun heltal "q" og "r", sådan at n = bq + r, hvor 0 ≤ r < |b|.

Tallet "n" kaldes et udbytte, "b" kaldes en skillevæg, "q" kaldes et kvotient og "r" kaldes resten eller resten. Når resten "r" er lig med 0 siges det at "b" deler "n", og dette betegnes med "b | n".

Opdelingsalgoritmen er ikke begrænset til positive værdier. Derfor kan et negativt tal være en skillevæg med et andet tal.

Hvorfor er 7,5 ikke en divisor på 30??

Ved hjælp af divisionsalgoritmen kan det ses, at 30 = 7,5 × 4 + 0. Resten er lig med nul, men det kan ikke siges, at 7,5 divideres med 30, for når vi taler om delere, taler vi kun om hele tal.

Skillevægge på 30

Som det kan ses på billedet, skal dets primære faktorer først findes for at finde delerne på 30.

Så 30 = 2x3x5. Ud fra dette konkluderer vi, at 2, 3 og 5 er delere på 30. Men det er også produkterne fra disse primære faktorer.

Så 2 × 3 = 6, 2 × 5 = 10, 3 × 5 = 15 og 2x3x5 = 30 er skillevægge på 30. 1 er også en skillevæg på 30 (skønt det faktisk er en skillevægge af ethvert tal).

Det kan konkluderes, at 1, 2, 3, 5, 6, 10, 15 og 30 er divisorer på 30 (alle overholder divisionsalgoritmen), men det skal huskes, at deres negativer også er divisorer.

Derfor er alle delere af 30: -30, -15, -10, -6, -5, -3, -2, -1, 1, 2, 3, 5, 6, 10, 15 og 30.

Det, der er lært ovenfor, kan anvendes på ethvert helt tal.

For eksempel, hvis du vil beregne delerne på 92, skal du fortsætte som før. Nedbrydes som et produkt af primtal.

Del 92 med 2 og få 46; divider nu 46 med 2 igen og få 23.

Dette sidste resultat er et primtal, så det vil ikke have flere delere udover 1 og det samme 23.

Vi kan derefter skrive 92 = 2x2x23. Forløber som før, konkluderes det, at 1,2,4,46 og 92 er delere af 92.

Endelig er negativerne af disse tal inkluderet i den forrige liste, hvor listen over alle divisorer på 92 er -92, -46, -4, -2, -1, 1, 2, 4, 46, 92.

Referencer

1. Barrantes, H., Díaz, P., Murillo, M., & Soto, A. (1988). Introduktion til talteori. San José: EUNED.
2. Bustillo, A. F. (1866). Matematiske elementer. Imp. Af Santiago Aguado.
3. Guevara, M. H. (s.f.). Talteori. San José: EUNED.
4. J., A. C., & A., L. T. (1995). Sådan udvikles matematisk logisk begrundelse. Santiago de Chile: Redaktionel Universitaria.
5. Jiménez, J., Delgado, M., & Gutiérrez, L. (2007). Guide Think II. Tærskeludgaver.
6. Jiménez, J., Teshiba, M., Teshiba, M., Romo, J., Álvarez, M., Villafania, P., Nesta, B. (2006). Matematik 1 Aritmetik og præalgebra. Tærskeludgaver.
7. Johnsonbaugh, R. (2005). Diskret matematik. Pearson Uddannelse.