
Samlede dataeksempler og øvelse løst
Det grupperede data er dem, der er klassificeret i kategorier eller klasser, idet deres hyppighed er et kriterium. Dette gøres for at forenkle håndteringen af store datamængder og etablere dens tendenser..
Når de er organiseret i disse klasser efter deres frekvenser, udgør dataene en frekvensfordeling, hvorfra nyttige oplysninger udvindes gennem dens egenskaber.

Her er et simpelt eksempel på grupperede data:
Antag, at højden på 100 kvindelige studerende, valgt fra alle de grundlæggende fysik-kurser på et universitet, måles, og følgende resultater opnås:

De opnåede resultater blev opdelt i 5 klasser, som vises i venstre kolonne.
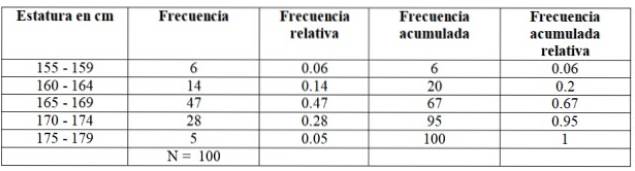
Den første klasse, mellem 155 og 159 cm, har 6 elever, den anden klasse 160 - 164 cm har 14 elever, den tredje klasse på 165 til 169 cm har det største antal medlemmer: 47. Derefter fortsætter klassen 170-174 cm med 28 studerende og endelig 175-174 cm med kun 5.
Antallet af medlemmer i hver klasse er netop antallet frekvens eller Absolut frecuency og når du tilføjer dem alle, opnås de samlede data, som i dette eksempel er 100.
Artikelindeks
- 1 Kendetegn for frekvensfordelingen
- 1.1 Frekvens
- 1.2 Grænser
- 1.3 Grænser
- 1.4 Amplitude
- 1.5 Klassemærke
- 2 Mål for central tendens og spredning for grupperede data
- 2.1 Gennemsnit
- 2.2 Median
- 2.3 Mode
- 2.4 Afvigelse og standardafvigelse
- 3 Øvelse løst
- 3.1 Løsning a
- 3.2 Løsning b
- 3.3 Løsning d
- 4 Referencer
Karakteristik af frekvensfordelingen
Frekvens
Som vi har set, er frekvensen det antal gange, et stykke data gentages. Og for at lette beregningerne af fordelingsegenskaberne, såsom gennemsnit og varians, defineres følgende størrelser:
-Kumulativ frekvens: det opnås ved at tilføje frekvensen for en klasse med den tidligere akkumulerede frekvens. Den første af alle frekvenser matcher frekvensen for det pågældende interval, og den sidste er det samlede antal data.
-Relativ frekvens: beregnes ved at dividere den absolutte frekvens for hver klasse med det samlede antal data. Og hvis du ganger med 100, har du den relative procentfrekvens.
-Kumulativ relativ frekvens: er summen af de relative frekvenser for hver klasse med den tidligere akkumulerede. Den sidste af de akkumulerede relative frekvenser skal være lig med 1.
For vores eksempel ser frekvenserne sådan ud:
Grænser
De ekstreme værdier for hver klasse eller interval kaldes klassegrænser. Som vi kan se, har hver klasse en lavere og en højere grænse. For eksempel har den første klasse i undersøgelsen om højder en nedre grænse på 155 cm og en højere grænse på 159 cm..
Dette eksempel har grænser, der er klart definerede, men det er muligt at definere åbne grænser: hvis du i stedet for at definere de nøjagtige værdier, siger "højde mindre end 160 cm", "højde mindre end 165 cm" og så videre.
Grænser
Højde er en kontinuerlig variabel, så det kan overvejes, at første klasse faktisk starter ved 154,5 cm, da afrunding af denne værdi til nærmeste heltal giver 155 cm.
Denne klasse dækker alle værdier op til 159,5 cm, for efter dette afrundes højderne til 160,0 cm. En højde på 159,7 cm hører allerede til følgende klasse.
De faktiske klassegrænser for dette eksempel er i cm:
- 154,5 - 159,5
- 159,5 - 164,5
- 164,5 - 169,5
- 169,5 - 174,5
- 174,5 - 179,5
Amplitude
Bredden på en klasse opnås ved at trække grænserne. I det første interval i vores eksempel har vi 159,5 - 154,5 cm = 5 cm.
Læseren kan kontrollere, at amplituden for de øvrige intervaller i eksemplet også er 5 cm. Det skal dog bemærkes, at distributioner kan konstrueres med intervaller med forskellig amplitude.
Klassemærke
Det er midtpunktet for intervallet og opnås ved gennemsnittet mellem den øvre grænse og den nedre grænse.
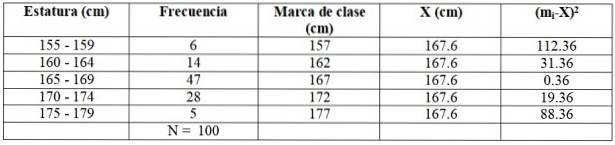
For vores eksempel er det første klassemærke (155 + 159) / 2 = 157 cm. Læseren kan se, at de resterende klassemarkeringer er: 162, 167, 172 og 177 cm.
Det er vigtigt at bestemme klassemarkeringerne, da de er nødvendige for at finde det aritmetiske gennemsnit og fordelingen af fordelingen.
Foranstaltninger for central tendens og spredning for samlede data
De mest anvendte målinger af central tendens er middelværdien, medianen og tilstanden, og de beskriver nøjagtigt datatendens tendens til at samle sig omkring en bestemt central værdi..
Halvt
Det er et af de vigtigste mål for central tendens. I de grupperede data kan det aritmetiske gennemsnit beregnes ved hjælp af formlen:

-X er middelværdien
-Fjeg er klassens frekvens
-mjeg er klassemærket
-g er antallet af klasser
-n er det samlede antal data
Median
For medianen er det nødvendigt at identificere det interval, hvor observationen n / 2 findes. I vores eksempel er denne observation nummer 50, fordi der i alt er 100 datapunkter. Denne observation er i området 165-169 cm.
Derefter skal du interpolere for at finde den numeriske værdi, der svarer til den observation, som formlen bruges til:

Hvor:
-c = bredde på det interval, hvor medianen findes
-BM = den nedre grænse for det interval, som medianen hører til
-Fm = antal observationer indeholdt i medianintervallet
-n / 2 = halvdelen af de samlede data
-FBM = det samlede antal observationer Før medianinterval
mode
For tilstanden identificeres den modale klasse, den der indeholder flest observationer, hvis klassemærke er kendt.
Variation og standardafvigelse
Variansen og standardafvigelsen er målinger af spredning. Hvis vi betegner variansen med sto og standardafvigelsen, som er kvadratroden af variansen som s, for grupperede data vil vi have henholdsvis:

Y

Træning løst
For at fordele højderne på kvindelige universitetsstuderende, der blev foreslået i starten, beregnes værdierne for:
a) Gennemsnit
b) Median
c) Mode
d) Afvigelse og standardafvigelse.

Løsning til
Lad os bygge følgende tabel for at lette beregningerne:


Udskiftning af værdier og direkte summering:
X = (6 x 157 + 14 x 162 + 47 x 167 + 28 x 172+ 5 x 177) / 100 cm =
= 167,6 cm
Løsning b
Intervallet, som medianen tilhører, er 165-169 cm, fordi det er intervallet med den højeste frekvens.

Lad os identificere hver af disse værdier i eksemplet ved hjælp af tabel 2:
c = 5 cm (se amplitudeafsnittet)
BM = 164,5 cm
Fm = 47
n / 2 = 100/2 = 50
FBM = 20
Udskiftning i formlen:
Intervallet, der indeholder de fleste observationer, er 165-169 cm, hvis klassemærke er 167 cm.
Løsning d
Vi udvider den forrige tabel ved at tilføje yderligere to kolonner:

Vi anvender formlen:

Og vi udvikler summeringen:
sto = (6 x 112,36 + 14 x 31,36 + 47 x 0,36 + 28 x 19,36 + 5 x 88,36) / 99 = = 21,35 cmto
Derfor:
s = √21,35 cmto = 4,6 cm
Referencer
- Berenson, M. 1985. Statistik for ledelse og økonomi. Interamericana S.A.
- Canavos, G. 1988. Sandsynlighed og statistik: Anvendelser og metoder. Mcgraw bakke.
- Devore, J. 2012. Sandsynlighed og statistik for ingeniørvidenskab og videnskab. 8. plads Udgave. Cengage.
- Levin, R. 1988. Statistik for administratorer. 2. plads Udgave. Prentice hall.
- Spiegel, M. 2009. Statistik. Schaum-serien. 4. plads Udgave. Mcgraw bakke.
- Walpole, R. 2007. Sandsynlighed og statistik for ingeniørvidenskab og videnskab. Pearson.



Endnu ingen kommentarer