
Implicit derivater, hvordan de løses og øvelser løses
Det implicitte derivater De er værktøjer, der anvendes i en differentieringsteknik, der anvendes på funktioner. De anvendes, når det ikke er muligt under almindelige metoder at rydde den afhængige variabel, der skal afledes. Denne godkendelse udføres på baggrund af den uafhængige variabel.
For eksempel i udtrykket 3xy3 - 2y + xyto = xy, du kan ikke få det udtryk, der definerer “y” som en funktion af “x”. Således ved at udlede det differentielle udtryk kan dy / dx opnås.

Artikelindeks
- 1 Hvordan løses implicitte derivater??
- 2 Kæde regel
- 3 Driftsordre
- 4 Implicit af en funktion
- 5 Historie
- 6 applikationer
- 7 Løst øvelser
- 7.1 Øvelse 1
- 7.2 Øvelse 2
- 8 Referencer
Hvordan løses implicitte derivater?
For at løse et implicit derivat starter vi med et implicit udtryk. For eksempel: 3xy3 - 2y + xyto - xy = 0. Dette er allerede løst korrekt, men det er dog ikke en nødvendig betingelse for at opnå derivatet af y med hensyn til x. Derefter udledes hvert af elementerne under overholdelse af kædereglen for blandede funktioner:
3xy3 består af 2 variabler, derfor er d (3xy3) behandles som afledt af et produkt af funktioner.
d (3xy3) / dx = 3 år3 + 3 årto.(3x) y '= 3 år3 + 9xyto Y '
Hvor elementet y 'er kendt som “og fætter”Y repræsenterer dy / dx
-2y Det er afledt i henhold til loven K.U = K.U '
d (-2y) = -2 y '
xyto antager en anden differentiel sammensat af et produkt af funktioner
d (xyto) = ogto + 2xy og '
-x og behandles homologt
d (-xy) = -y - x y '
De er substitueret i lighed, vel vidende at derivatet af nul er nul.
3 år3 + 9xyto y '- 2 y' + yto + 2xy y '- y - x y' = 0
De elementer, der har betegnelsen y ', er grupperet på den ene side af ligestillingen
3 år3 + Yto - y = -9xyto y '+ 2 y' + x y '
Den fælles faktor y 'udvindes i højre side af ligestillingen
3 år3 + Yto - y = y '(-9xyto + x + 2)
Endelig ryddes udtrykket, der multiplicerer y '. Således opnås udtrykket svarende til det implicitte derivat af y med hensyn til x.
y '= dy / dx = (3y3 + Yto - y) / (- 9xyto + x + 2)
Kæde regel
Ved implicit afledning respekteres kædereglen altid. Alle differentielle udtryk gives som en funktion af den uafhængige variabel X. Så enhver variabel variable bortset fra X, skal omfatte udtrykket dθ / dx efter at være afledt.
Dette udtryk vises kun i første grad eller med en eksponent svarende til 1. Denne kvalitet gør det helt klart under traditionelle factoring-metoder. Det er således muligt at opnå det udtryk, der definerer differencen dθ / dx.
Kædereglen viser den progressive karakter af differentieringen eller den afledte proces. Hvor for hver sammensatningsfunktion f [g (x)], har vi, at den differentielle ekspression af f vil være
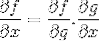
Driftsordre
I hver formel eller afledningslov, der anvendes, skal rækkefølgen af variablerne indbyrdes tages i betragtning. Kriterierne forbundet med den uafhængige variabel respekteres uden at ændre dens korrelation med den afhængige variabel..
Forholdet mellem den afhængige variabel på afledningstidspunktet tages direkte; med den undtagelse, at dette vil blive betragtet som en anden funktion, hvorfor kæderegelkriteriet anvendes for blandede funktioner.
Dette kan udvikles i udtryk med mere end 2 variabler. Under de samme principper vil alle forskelle, der henviser til de afhængige variabler, blive betegnet.
Grafisk håndteres det samme kriterium, der definerer derivatet. Mens derivatet er hældningen af tangentlinjen til kurven i planet, repræsenterer resten af differentierne, der hører til de afhængige variabler (dy / dx, dz / dx), planer, der er tangent til vektorlegemerne beskrevet af de flere variable funktioner.
Implicit af en funktion
En funktion siges at være implicit defineret, hvis udtrykket y = f (x) kan repræsenteres som en multipel variabel funktion F (x, y) = 0, så længe F er defineret i R-planetto.
3xy3 - 2y + xyto = xy kan skrives i form 3xy3 - 2y + xyto - xy = 0
I betragtning af umuligheden af at eksplicere funktionen y = f (x).
Historie
Differentialregningen begyndte at blive navngivet af forskellige matematiske forskere omkring det syttende århundrede. Første gang det blev nævnt var gennem bidrag fra Newton og Leibniz. Begge behandlede differentieringsberegningen fra forskellige synsvinkler, men konvergerede i deres resultater.
Mens Newton fokuserede på differentiering som en hastighed eller forandringshastighed, var Leibniz tilgang mere geometrisk. Det kan siges, at Newton angreb de formodninger, som Apollonius fra Perge og Leibniz efterlod de geometriske ideer fra Fermat..
Den implicitte afledning vises straks, når man overvejer de differentielle og integrale ligninger. Disse udvidede Leibniz geometriske koncept til R3 og endda flerdimensionelle rum.
Ansøgninger
Implicitte derivater anvendes i forskellige situationer. De er almindelige i valutakursproblemer mellem relaterede variabler, hvor variablerne afhængigt af undersøgelsens mening vil blive betragtet som afhængige eller uafhængige..
De har også interessante geometriske anvendelser, såsom i refleksions- eller skyggeproblemer, på figurer, hvis form kan matematisk modelleres..
De bruges ofte inden for økonomi og teknik såvel som i forskellige undersøgelser af naturfænomener og eksperimentelle bygninger..
Løst øvelser
Øvelse 1
Definer det implicitte udtryk, der definerer dy / dx
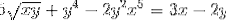
Hvert element i udtrykket er differentieret
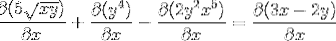
Fastsættelse af kædereglen i hvert kompetent tilfælde
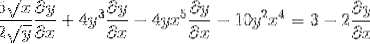
Gruppering af den ene side af lighed de elementer, der har dy / dx
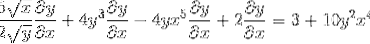
Det tages med den fælles faktor
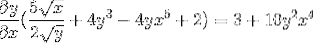
Det løses ved at opnå det ønskede udtryk
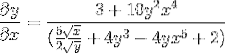
Øvelse 2
Definer det implicitte udtryk, der definerer dy / dx
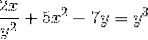
Udtrykker de derivater, der skal udføres
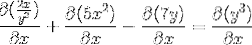
Deriverer implicit i henhold til kæderegel
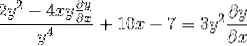
Faktorering af fælles elementer
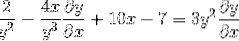
Gruppering af udtrykket dy / dx på den ene side af ligestillingen
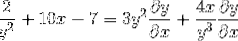
Fælles faktor for differentieringselementet
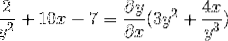
Vi isolerer og opnår det ønskede udtryk
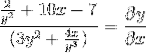
Referencer
- Beregning af en enkelt variabel. Ron Larson, Bruce H. Edwards. Cengage Learning, 10. nov 2008
- The Implicit Function Theorem: History, Theory, and Applications. Steven G. Krantz, Harold R. Parks. Springer Science & Business Media, 9. nov. 2012
- Multivariabel analyse. Satish Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13. dec. 2010
- Systemdynamik: Modellering, simulering og kontrol af mekatroniske systemer. Dean C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7. mar 2012
- Calculus: Matematik og modellering. William Bauldry, Joseph R. Fiedler, Frank R. Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1. jan 1999



Endnu ingen kommentarer