
Forskel mellem terningformler, ligninger, eksempler, øvelser
Det forskel på terninger er et binomialt algebraisk udtryk for formen a3 - b3, hvor udtrykkene a og b kan være reelle tal eller algebraiske udtryk af forskellige typer. Et eksempel på en forskel på terninger er: 8 - x3, da 8 kan skrives som 23.
Geometrisk kan vi tænke på en stor terning med side a, hvorfra den lille terning med side b trækkes fra, som illustreret i figur 1:
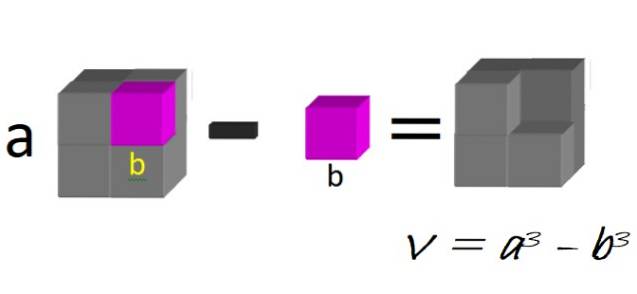
Volumenet af den resulterende figur er netop en forskel på terninger:
V = a3 - b3
For at finde et alternativt udtryk observeres det, at denne figur kan nedbrydes i tre prismer, som vist nedenfor:
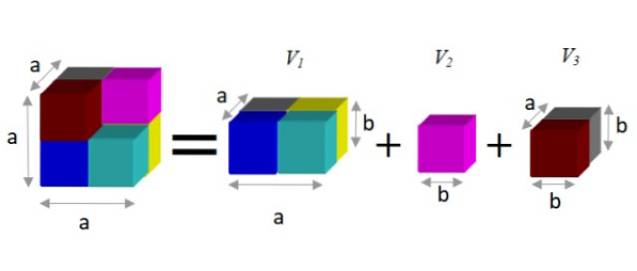
Et prisme har et volumen givet af produktet i dets tre dimensioner: bredde x højde x dybde. På denne måde er det resulterende volumen:
V = a3 - b3 = ato.b + b3 + a.bto
Faktoren b det er fælles til højre. Ydermere er det i ovenstående figur især rigtigt, at:
b = (a / 2) ⇒ a = b + b
Derfor kan det siges, at: b = a - b. Dermed:
til3 - b3 = b (ato + bto +a.b) = (a-b) (ato + a.b + bto)
Denne måde at udtrykke forskellen på terninger på vil vise sig at være meget nyttig i mange applikationer og ville være opnået på samme måde, selvom siden af den manglende terning i hjørnet var forskellig fra b = a / 2.
Bemærk, at den anden parentesligner meget det bemærkelsesværdige produkt af summen, men krydsudtrykket ganges ikke med 2. Læseren kan udvikle den rigtige side for at kontrollere, at den faktisk opnås til3 - b3.
Artikelindeks
- 1 Eksempler
- 1.1 Faktorering af en forskel på terninger
- 2 Øvelse løst
- 2.1 Øvelse 1
- 2.2 Øvelse 2
- 3 Referencer
Eksempler
Der er flere forskelle i terninger:
1 - m6
til6b3 - 8z12Y6
(1/125) .x6 - 27 og9
Lad os undersøge hver enkelt af dem. I det første eksempel kan 1 skrives som 1 = 13 og udtrykket m6 forbliver: (mto)3. Begge termer er perfekte terninger, derfor er deres forskel:
1 - m6 = 13 - (mto)3
I det andet eksempel omskrives udtrykkene:
til6b3 = (atob)3
8z12Y6 = 23 (z4)3 (Yto)3 = (2z4Yto)3
Forskellen mellem disse terninger er: (atob)3 - (2z4Yto)3.
Endelig er brøkdelen (1/125) (1/53), x6 = (xto)3, 27 = 33 og og9 = (og3)3. Ved at erstatte alt dette i det originale udtryk får du:
(1/125) .x6 - 27 år9 = [(1/5) (xto)]3 - (3 år3)3
Faktorering af en forskel på terninger
At faktorisere forskellen på terninger forenkler mange algebraiske operationer. For at gøre dette er det nok at bruge formlen udledt ovenfor:

Nu består proceduren for anvendelse af denne formel af tre trin:
- For det første opnås terningen af hver af forskelsbetingelserne.
- Derefter konstrueres binomialet og trinomialet, der vises på højre side af formlen.
- Endelig erstattes binomialet og trinomialet for at opnå den endelige faktorisering.
Lad os illustrere brugen af disse trin med hvert af de ovenfor anførte terningsforskelleeksempler og dermed opnå dets fakturerede ækvivalent.
Eksempel 1
Faktor udtryk 1 - m6 ved at følge de beskrevne trin. Vi starter med at omskrive udtrykket som 1 - m6 = 13 - (mto)3 for at udtrække de respektive terningsrødder for hvert udtryk:


Dernæst konstrueres binomialet og trinomialet:
a = 1
b = mto
Derefter:
a - b = 1 - mto
(tilto +a.b + bto) = 1to + 1.mto + (mto)to = 1 + mto + m4
Endelig er det substitueret i formlen a3 - b3 = (a-b) (ato +a.b + bto):
1 - m6 = (1 - mto) (1 + mto + m4)
Eksempel 2
Faktoriser:
til6b3 -8z12Y6 = (atob)3 - (2z4Yto)3
Da disse er perfekte terninger, er terningrødderne øjeblikkelige: atob og 2z4Yto, det følger heraf, at:
- Binomial: atob - 2z4Yto
- Trinomial: (atob)to + tiltob. 2z4Yto + (tiltob + 2z4Yto)to
Og nu er den ønskede faktorisering konstrueret:
til6b3 -8z12Y6 = (atob - 2z4Yto). [(tiltob)to + tiltob. 2z4Yto + (tiltob + 2z4Yto)to] =
= (atob - 2z4Yto). [til4bto + 2. pladstob.z.4Yto + (tiltob + 2z4Yto)to]
I princippet er factoring klar, men det er ofte nødvendigt at forenkle hver periode. Derefter udvikler vi det bemærkelsesværdige produkt-kvadrat af et beløb- der vises i slutningen og tilføjer derefter lignende udtryk. Husk at kvadratet af en sum er:
(x + y)to = xto + 2xy + ogto
Det bemærkelsesværdige produkt til højre er udviklet således:
(tiltob + 2z4Yto)to = a4bto + 4. pladstob.z.4Yto + 4z8Y4
Udskiftning af ekspansion opnået i faktorisering af forskellen i terninger:
til6b3 -8z12Y6 = (atob - 2z4Yto). [til4bto + 2. pladstob.z.4Yto + til4bto + 4. pladstob.z.4Yto + 4z8Y4] =
Endelig får vi gruppering af lignende termer og faktorering af de numeriske koefficienter, som alle er ens:
(tiltob - 2z4Yto). [2a4bto + 6.tob.z.4Yto + 4z8Y4] = 2 (atob - 2z4Yto). [til4bto + 3.tob.z.4Yto + 2z8Y4]
Eksempel 3
Faktor (1/125) .x6 - 27 år9 det er meget enklere end det foregående tilfælde. Først identificeres ækvivalenterne af a og b:
a = (1/5) xto
b = 3 år3
Derefter erstattes de direkte i formlen:
(1/125) .x6 - 27 år9 = [(1/5) xto - 3 år3]. [(1/25) x4 + (3/5) xtoY3 + 9 år6]
Træning løst
Forskellen i terninger har, som vi har sagt, en række anvendelser i Algebra. Lad os se nogle:
Øvelse 1
Løs følgende ligninger:
a) x5 - 125 xto = 0
b) 64 - 729 x3 = 0
Løsning til
Først er ligningen beregnet på denne måde:
xto (x3 - 125) = 0
Da 125 er en perfekt terning, skrives parenteserne som en forskel i terninger:
xto . (x3 - 53) = 0
Den første løsning er x = 0, men vi finder mere, hvis vi gør x3 - 53 = 0, derefter:
x3 = 53 → x = 5
Løsning b
Venstre side af ligningen omskrives som 64 - 729 x3 = 43 - (9x)3. Derfor:
43 - (9x)3 = 0
Da eksponenten er den samme:
9x = 4 → x = 9/4
Øvelse 2
Faktor for udtrykket:
(x + y)3 - (x - y)3
Opløsning
Dette udtryk er en forskel på terninger, hvis vi i factoringformlen bemærker, at:
a = x + y
b = x- y
Derefter konstrueres binomialet først:
a - b = x + y - (x- y) = 2y
Og nu trinomialet:
tilto + a.b + bto = (x + y)to + (x + y) (x-y) + (x-y)to
Bemærkelsesværdige produkter er udviklet:
(x + y)to = xto + 2xy + ogto
(x + y) (x-y) = xto- Yto
(x- y)to = xto - 2xy + ogto
Dernæst skal du erstatte og reducere lignende udtryk:
tilto + a.b + bto = xto + 2xy + ogto+ xto- Yto+ xto - 2xy + ogto = 3xto + Yto
Faktoring resulterer i:
(x + y)3 - (x - y)3 = 2 år. (3xto + Yto)
Referencer
- Baldor, A. 1974. Algebra. Redaktionel Cultural Venezolana S.A.
- CK-12 Foundation. Sum og forskel på terninger. Gendannet fra: ck12.org.
- Khan Academy. Faktoring af forskelle i terninger. Gendannet fra: es.khanacademy.org.
- Matematik er sjovt avanceret. Forskel på to terninger. Gendannet fra: mathsisfun.com
- UNAM. Faktorering af en forskel på terninger. Gendannet fra: dcb.fi-c.unam.mx.



Endnu ingen kommentarer