Forskel mellem en fælles brøk og et decimaltal

At identificere hvad er forskellen mellem en fælles brøk og et decimaltal det er nok at observere begge elementer: det ene repræsenterer et rationelt tal, og det andet inkluderer i sin konstitution en hel del og en decimaldel.

En "almindelig brøkdel" er udtryk for en størrelse divideret med en anden uden at udføre den deling. Matematisk er en fælles brøk et rationelt tal, der defineres som kvotienten for to hele tal “a / b”, hvor b ≠ 0.

Et "decimaltal" er et tal, der består af to dele: et heltal og en decimaldel..

For at adskille heltalets del fra decimaldelen placeres et komma kaldet et decimaltegn, selvom der også bruges en periode afhængigt af bibliografien.

Decimaltal

Et decimaltal kan have et endeligt eller uendeligt antal tal i sin decimaldel. Det uendelige antal decimaler kan også nedbrydes i to typer:

Periodisk

Det vil sige, det har et gentaget mønster. For eksempel 2.454545454545…

Ikke periodisk

De har intet gentaget mønster. For eksempel 1.7845265397219 ...

Tal der har et periodisk uendeligt eller uendeligt antal decimaler kaldes rationelle tal, mens de der har et ikke-periodisk uendeligt antal kaldes irrationelle.

Foreningen af ​​sættet med rationelle tal og sættet med irrationelle tal er kendt som sættet med reelle tal.

Forskelle mellem almindelig brøkdel og decimaltal

Forskellene mellem en fælles brøk og et decimaltal er:

1- Decimal del

Hver almindelig brøkdel har et endeligt antal tal i sin decimaldel eller et uendeligt periodisk tal, mens et decimaltal kan have et uendeligt ikke-periodisk antal tal i sin decimaldel..

Ovenstående siger, at hvert rationelt tal (hver fælles brøk) er et decimaltal, men ikke hvert decimaltal er et rationelt tal (en fælles brøk).

2- Notation

Hver almindelig fraktion er betegnet som kvotienten for to hele tal, mens et irrationelt decimaltal ikke kan betegnes på denne måde..

De mest anvendte irrationelle decimaltal i matematik er angivet med kvadratrødder (√ ), kubisk (³√ ) og højere karakterer.

Udover disse er der to meget berømte numre, som er Euler-nummeret, betegnet med e; og tallet pi, betegnet med π.

Sådan går du fra en fælles brøk til et decimaltal?

For at gå fra en fælles brøk til et decimaltal skal du bare lave den tilsvarende opdeling. Hvis du f.eks. Har 3/4, er det tilsvarende decimaltal 0,75.

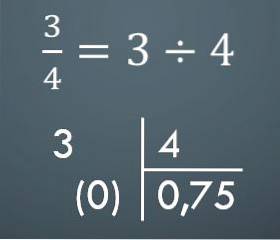
Sådan går du fra et rationelt decimaltal til en fælles brøk?

Den omvendte proces til den foregående kan også udføres. Følgende eksempel illustrerer en teknik til at flytte fra et rationelt decimaltal til en fælles brøk:

- Lad x = 1,78

Da x har to decimaler, multipliceres den tidligere ligestilling med 10² = 100, hvormed vi får 100x = 178; og at løse for x resulterer i, at x = 178/100. Dette sidste udtryk er den almindelige brøk, der repræsenterer tallet 1,78.

Men kan denne proces udføres for tal med et periodisk uendeligt antal decimaler? Svaret er ja, og det følgende eksempel viser de trin, der skal følges:

- Lad x = 2.193193193193 ...

Da perioden med dette decimaltal har 3 cifre (193) multipliceres det foregående udtryk med 10³ = 1000, hvormed vi får udtrykket 1000x = 2193.193193193193 ... .

Nu trækkes det sidste udtryk fra det første, og hele decimaldelen annulleres og efterlader udtrykket 999x = 2191, hvorfra vi opnår, at den fælles brøkdel er x = 2191/999.

Referencer

1. Anderson, J. G. (1983). Teknisk butik matematik (Illustreret red.). Industrial Press Inc..
2. Avendaño, J. (1884). Komplet manual til grundlæggende og højere grundlæggende instruktioner: til brug af håbefulde lærere og især studerende fra provinsens normale skoler (2. udgave, bind 1). Trykning af D. Dionisio Hidalgo.
3. Coates, G. og. (1833). Den argentinske aritmetik: Komplet afhandling om praktisk aritmetik. Til brug af skoler. Print af staten.
4. Fra havet. (1962). Matematik til workshoppen. Vend tilbage.
5. DeVore, R. (2004). Praktiske problemer i matematik til varme- og køleteknikere (Illustreret red.). Cengage læring.
6. Jariez, J. (1859). Komplet kursus i fysiske og mekaniske matematiske videnskaber anvendt til industriel kunst (2. udgave). Jernbanetrykkeri.
7. Palmer, C. I., & Bibb, S. F. (1979). Praktisk matematik: aritmetik, algebra, geometri, trigonometri og slide-regel (genudskrivning red.). Vend tilbage.