Det Euklidisk afstand er et positivt tal, der angiver adskillelsen mellem to punkter i et rum, hvor aksiomerne og sætningerne i Euklids geometri er opfyldt.
Afstanden mellem to punkter A og B i et euklidisk rum er vektorens længde AB tilhører den eneste linje, der passerer gennem disse punkter.
Det rum, vi opfatter, og hvor vi mennesker bevæger os, er et tredimensionelt rum (3-D), hvor aksiomerne og sætningerne i Euklids geometri er opfyldt. To-dimensionelle underrum (plan) og endimensionelle underrum (linjer) er indeholdt i dette rum..
Euklidiske rum kan være endimensionale (1-D), to-dimensionelle (2-D), tredimensionelle (3-D) eller n-dimensionelle (n-D).
Punkter i det endimensionelle rum X er dem, der hører til den orienterede linje (OX), retningen fra O til X er den positive retning. For at lokalisere punkterne på denne linje anvendes det cartesianske system, som består i at tildele hvert punkt på linjen et tal.
Artikelindeks
Den euklidiske afstand d (A, B) mellem punkterne A og B, placeret på en linje, er defineret som kvadratroden af kvadratet af forskellene i deres X-koordinater:
d (A, B) = √ ((XB - XA) ^ 2)
Denne definition garanterer, at: afstanden mellem to punkter altid er en positiv størrelse. Og at afstanden mellem A og B er lig med afstanden mellem B og A..
Figur 1 viser det endimensionelle euklidiske rum dannet af linjen (OX) og flere punkter på linjen. Hvert punkt har en koordinat:
Punkt A har koordinat XA = 2,5, punkt B koordinat XB = 4 og punkt C koordinat XC = -2,5
d (A, B) = √ ((4 - 2,5) 2) = 1,5
d (B, A) = √ ((2,5 - 4) 2) = 1,5
d (A, C) = √ ((- 2,5 - 2,5) 2) = 5,0
To-dimensionelt euklidisk rum er et plan. Punktene på et euklidisk plan opfylder aksiomerne i Euklids geometri, for eksempel:
- En enkelt linje passerer gennem to punkter.
- Tre punkter på planet danner en trekant, hvis indre vinkler altid udgør 180º.
- I en højre trekant er hypotenusens firkant lig med summen af firkanterne på benene.
I to dimensioner har et punkt X- og Y-koordinater.
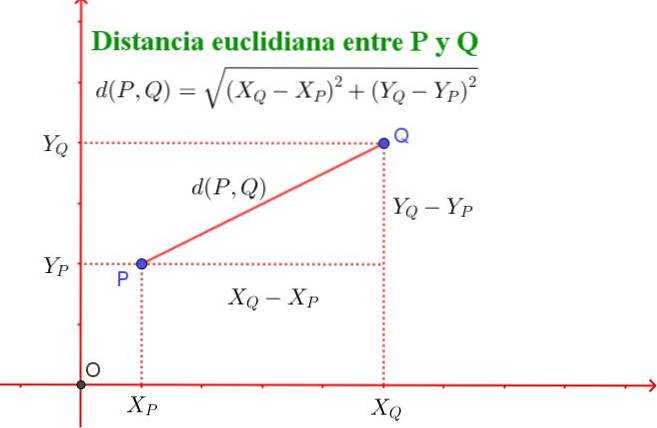
For eksempel har et punkt P koordinater (XP, YP) og et punkt Q koordinater (XQ, YQ).
Den euklidiske afstand mellem punkt P og Q er defineret med følgende formel:
d (P, Q) = √ ((XQ - XP) ^ 2 + (YQ - YP) ^ 2)
Det skal bemærkes, at denne formel svarer til Pythagoras sætning, som vist i figur 2.
Ikke alle to-dimensionelle rum svarer til den euklidiske geometri. Kuglens overflade er et todimensionelt rum.
Vinklerne på en trekant på en sfærisk overflade tilføjes ikke op til 180 º, og dermed opfyldes den pythagoriske sætning ikke, derfor opfylder en sfærisk overflade ikke Euklids aksiomer.
Begrebet koordinater kan udvides til større dimensioner:
- I 2-D punkt har P koordinater (XP, YP)
- I 3-D har et punkt Q koordinater (XQ, YQ, ZQ)
- I 4-D punkt vil R have koordinater (XR, YR, ZR, WR)
- I n-D vil et punkt P have koordinater (P1, P2, P3,…, Pn)
Afstanden mellem to punkter P og Q i et n-dimensionelt euklidisk rum beregnes med følgende formel:
d (P, Q) = √ ((Q1 - P1) ^ 2 + (Q2 - P2) ^ 2 + ... + (Qn - Pn) ^ 2)
Stedet for alle punkter Q i et n-dimensionelt euklidisk rum, der er lige langt fra et andet fast punkt P (midten), danner en n-dimensionel hypersfære.
Det følgende viser, hvordan afstanden mellem to punkter i det euklidiske tredimensionelle rum beregnes.
Antag punkt A af kartesiske koordinater x, y, z givet af A :( 2, 3, 1) og punkt B for koordinater B :( -3, 2, 2).
Vi ønsker at bestemme afstanden mellem disse punkter, som det generelle forhold bruges til:
d (A, B) = √ ((-3 - 2) 2 + (2-3) 2 + (2 - 1) 2) = √ ((-5) 2 + (-1) 2 + (1) 2 )
d (A, B) = √ (25 + 1 + 1) = √ (27) = √ (9 * 3) = 3 √ (3) = 5.196
Der er to punkter P og Q. Punktet P for de kartesiske koordinater x, y, z givet af P :( 2, 3, 1) og punktet Q for koordinaterne Q :( -3, 2, 1).
Det bliver bedt om at finde koordinaterne til midtpunktet M i segmentet [PQ], der forbinder de to punkter.
Opløsning:
Det ukendte punkt M antages at have koordinater (X, Y, Z).
Da M er midtpunktet for [PQ], skal det være sandt, at d (P, M) = d (Q, M), så d (P, M) ^ 2 = d (Q, M) ^ 2 også skal være sand :
(X - 2) ^ 2 + (Y - 3) ^ 2 + (Z - 1) ^ 2 = (X - (-3)) ^ 2 + (Y - 2) ^ 2 + (Z - 1) ^ 2
Som i dette tilfælde er den tredje periode ens i begge medlemmer, det foregående udtryk forenkles til:
(X - 2) ^ 2 + (Y - 3) ^ 2 = (X + 3) ^ 2 + (Y - 2) ^ 2
Vi har derefter en ligning med to ukendte X og Y. En anden ligning er nødvendig for at løse problemet.
Punkt M hører til linjen, der passerer gennem punkterne P og Q, som vi kan beregne som følger:
Først er instruktørvektoren PQ af den lige: PQ = < -3-2, 2-3, 1-1> = < -5, -1, 0 >.
Senere OM EFTERMIDDAGEN = OP + til PQ, hvor OP er positionsvektoren for punkt P og til er en parameter, der hører til de reelle tal.
Ovenstående ligning er kendt som linjens vektorligning, som i kartesiske koordinater har følgende form:
< X-2, Y-3, Z-1> = <2, 3, 1> + til < -5, -1, 0> = < 2 - 5a, 3 - a, 0>
Ligning med de tilsvarende komponenter, vi har:
X - 2 = 2-5 a; Y - 3 = 3 -a; Z - 1 = 0
Det vil sige X = 4 - 5a, Y = 6 - a, til sidst Z = 1.
Det er substitueret i det kvadratiske udtryk, der relaterer X til Y:
(4 - 5a - 2) ^ 2 + (6 - a - 3) ^ 2 = (4 - 5a + 3) ^ 2 + (6 - a - 2) ^ 2
Det er forenklet:
(2 - 5a) ^ 2 + (3 -a) ^ 2 = (7 - 5a) ^ 2 + (4 - a) ^ 2
Udfolder sig nu:
4 + 25 a ^ 2 - 20a + 9 + a ^ 2 - 6a = 49 + 25 a ^ 2 - 70a + 16 + a ^ 2 - 8a
Det er forenklet og annullerer lignende vilkår i begge medlemmer:
4 - 20a + 9 - 6a = 49 - 70a + 16 - 8a
Parameteren a ryddes:
52 a = 49 + 16 - 4 - 9 = 52 hvilket resulterer i at a = 1.
Det vil sige X = 4-5, Y = 6-1, til sidst Z = 1.
Endelig opnår vi de kartesiske koordinater for midtpunktet M for segmentet [PQ]:
M: (-1, 5, 1).
Endnu ingen kommentarer