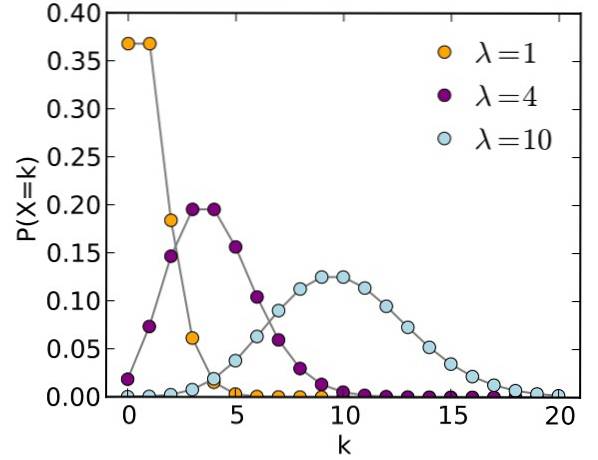
Det Poisson fordeling er en diskret sandsynlighedsfordeling, gennem hvilken det er muligt at kende sandsynligheden for, at der inden for en stor stikprøvestørrelse og i et bestemt interval opstår en begivenhed, hvis sandsynlighed er lille.
Ofte kan Poisson-fordelingen bruges i stedet for binomialfordelingen, så længe følgende betingelser er opfyldt: stor prøve og lille sandsynlighed.
Siméon-Denis Poisson (1781-1840) skabte denne distribution, der bærer hans navn, meget nyttig, når det kommer til uforudsigelige begivenheder. Poisson offentliggjorde sine resultater i 1837, et forskningsarbejde om sandsynligheden for forekomst af fejlagtige straffedomme.
Senere tilpassede andre forskere fordelingen i andre områder, for eksempel antallet af stjerner, der kunne findes i et bestemt rumvolumen, eller sandsynligheden for, at en soldat døde af et hestespark.
Artikelindeks
Den matematiske form for Poisson-fordelingen er som følger:
- μ (også undertiden betegnet som λ) er middelværdien eller parameteren for fordelingen
- Euler nummer: e = 2,71828
- Sandsynligheden for at opnå y = k er P
- k er antallet af succeser 0, 1,2,3 ...
- n er antallet af tests eller begivenheder (stikprøvestørrelsen)
Diskrete tilfældige variabler, som deres navn indikerer, afhænger af tilfældighed og tager kun diskrete værdier: 0, 1, 2, 3, 4 ..., k.
Fordelingens gennemsnit er givet ved:
Variansen σ, som måler spredningen af data, er en anden vigtig parameter. For Poisson-distributionen er det:
σ = μ
Poisson fastslog, at når n → ∞, og p → 0, kaldes gennemsnittet μ-også forventet værdi- har tendens til en konstant:
μ → konstant
Vigtig: s er sandsynligheden for begivenhedens forekomst under hensyntagen til den samlede befolkning, mens P (y) er Poisson-forudsigelsen på prøven.
Poisson-distributionen har følgende egenskaber:
-Prøvestørrelsen er stor: n → ∞.
-Begivenhederne eller begivenhederne, der betragtes, er uafhængige af hinanden og forekommer tilfældigt.
-Sandsynlighed P den bestemte begivenhed Y opstår i en bestemt periode er meget lille: P → 0.
-Sandsynligheden for, at der opstår mere end en begivenhed i tidsintervallet, er 0.
-Den gennemsnitlige værdi er omtrentlig en konstant givet af: μ = n.p (n er stikprøvestørrelsen)
-Da dispersionen σ er lig med μ, da den vedtager større værdier, bliver variationen også større.
-Begivenhederne skal fordeles jævnt i det anvendte tidsinterval.
-Sættet med mulige begivenhedsværdier Y er: 0,1,2,3,4 ... .
-Summen af jeg variabler, der følger en Poisson-fordeling, er også en anden Poisson-variabel. Dens gennemsnitlige værdi er summen af gennemsnitsværdierne for disse variabler.
Poisson-fordelingen adskiller sig fra binomialfordelingen på følgende vigtige måder:
-Binomialfordelingen påvirkes af både stikprøvestørrelse n og sandsynligheden P, men Poisson-fordelingen påvirkes kun af middelværdien μ.
-I en binomialfordeling er de mulige værdier for den tilfældige variabel Y er 0,1,2,…, N, på den anden side i Poisson-fordelingen er der ingen øvre grænse for disse værdier.
Poisson anvendte oprindeligt sin berømte distribution i juridiske sager, men på industrielt niveau var en af hans tidligste anvendelser i fremstilling af øl. I denne proces anvendes gærkulturer til gæring.
Gær består af levende celler, hvis population er variabel over tid. Ved fremstilling af øl er det nødvendigt at tilføje den nødvendige mængde, derfor er det nødvendigt at kende mængden af celler, der er pr. Volumenhed.
Under Anden Verdenskrig blev Poisson-distributionen brugt til at finde ud af, om tyskerne faktisk sigtede mod London fra Calais, eller bare skyder tilfældigt. Dette var vigtigt for de allierede at bestemme, hvor god teknologien var tilgængelig for nazisterne..
Anvendelserne af Poisson-distributionen henviser altid til tællinger i tid eller tællinger i rummet. Og da sandsynligheden for forekomst er lille, er den også kendt som "loven om sjældne begivenheder".
Her er en liste over begivenheder, der falder inden for en af disse kategorier:
-Registrering af partiklerne i et radioaktivt henfald, der ligesom væksten af gærceller er en eksponentiel funktion.
-Antal besøg på et bestemt websted.
-Ankomst af mennesker i en linje for at betale eller deltage (køteori).
-Antal biler, der passerer et bestemt punkt på en vej i et givet tidsinterval.
-Mutationer i en bestemt DNA-streng efter modtagelse af strålingseksponering.
-Antallet af meteoritter med en diameter større end 1 m faldet om året.
-Mangler pr. Kvadratmeter stof.
-Antal blodlegemer i 1 kubikcentimeter.
-Opkald pr. Minut til en telefoncentral.
-Chokoladechips til stede i 1 kg kagedej.
-Antal træer inficeret af en bestemt parasit i 1 hektar skov.
Bemærk, at disse tilfældige variabler repræsenterer antallet af gange, en begivenhed finder sted i en fast tidsperiode (opkald pr. minut til telefoncentralen) eller et givet område af rummet (defekter af et stof pr. kvadratmeter).
Disse begivenheder er, som allerede er etableret, uafhængige af den tid, der er gået siden den sidste begivenhed..
Poisson-fordelingen er en god tilnærmelse til binomialfordelingen, så længe:
-Prøvestørrelsen er stor: n ≥ 100
-Sandsynlighed p er lille: p ≤ 0,1
- μ er i rækkefølgen af: np ≤ 10
I sådanne tilfælde er Poisson-fordelingen et fremragende værktøj, da binomialfordelingen kan være vanskelig at anvende i disse tilfælde..
En seismologisk undersøgelse fastslog, at der i løbet af de sidste 100 år var 93 store jordskælv rundt om i verden, mindst 6,0 på Richter-skalaen -logaritmisk-. Antag, at Poisson-fordelingen er en passende model i dette tilfælde. Finde:
a) Den gennemsnitlige forekomst af store jordskælv om året.
b) Ja P (y) er sandsynligheden for forekomst Y jordskælv i løbet af et tilfældigt udvalgt år, find følgende sandsynligheder:
P(0), P(1), P (to), P (3), P (4), P (5), P (6) og P (7).
c) De sande resultater af undersøgelsen er følgende:
- 47 år (0 jordskælv)
- 31 år (1 jordskælv)
- 13 år (2 jordskælv)
- 5 år (3 jordskælv)
- 2 år (4 jordskælv)
- 0 år (5 jordskælv)
- 1 år (6 jordskælv)
- 1 år (7 jordskælv)
Hvordan sammenlignes disse resultater med resultaterne opnået i del b? Er Poisson-distributionen et godt valg at modellere disse begivenheder?
a) Jordskælv er begivenheder, hvis sandsynlighed s det er lille, og vi overvejer en begrænset periode på et år. Det gennemsnitlige antal jordskælv er:
μ = 93/100 jordskælv / år = 0,93 jordskælv pr. år.
b) For at beregne de ønskede sandsynligheder erstattes værdier i formlen i starten:
y = 2
μ = 0,93
e = 2,71828
Det er ret mindre end P (2).
Resultaterne er anført nedenfor:
P (0) = 0,395, P (1) = 0,367, P (2) = 0,171, P (3) = 0,0529, P (4) = 0,0123, P (5) = 0,00229, P (6) = 0,000355, P (7) = 0,0000471.
For eksempel kan vi sige, at der er en sandsynlighed på 39,5% for, at der ikke vil forekomme større jordskælv i et givet år. Eller at der forekommer 5,29% af 3 store jordskælv i det år.
c) Frekvenserne analyseres multipliceret med n = 100 år:
39,5; 36,7; 17.1; 5,29; 1,23; 0,229; 0,0355 og 0,00471.
For eksempel:
- En frekvens på 39,5 indikerer, at der i 39,5 ud af 100 år opstår 0 store jordskælv, vi kunne sige, at det er ret tæt på det faktiske resultat på 47 år uden noget større jordskælv..
Lad os sammenligne et andet Poisson-resultat med de faktiske resultater:
- Den opnåede værdi på 36,7 betyder, at der i en periode på 37 år er et stort jordskælv. Det faktiske resultat er, at der i 31 år var 1 større jordskælv, hvilket passer godt sammen med modellen.
- Der forventes 17,1 år med 2 store jordskælv, og det vides, at der i 13 år, hvilket er en tæt værdi, faktisk var 2 store jordskælv.
Derfor er Poisson-modellen acceptabel i denne sag.
Et selskab vurderer, at antallet af komponenter, der fejler, inden de når 100 driftstimer, følger en Poisson-distribution. Hvis det gennemsnitlige antal fejl er 8 på det tidspunkt, skal du finde følgende sandsynligheder:
a) At en komponent fejler om 25 timer.
b) Fejl på mindre end to komponenter inden for 50 timer.
c) Svigt af mindst tre komponenter på 125 timer.
a) Det vides, at gennemsnittet af fiaskoer i 100 timer er 8, og derfor forventes der i 25 timer en fjerdedel af fiaskoer, dvs. 2 fejl. Dette vil være parameteren μ.
Der kræves sandsynligheden for, at 1 komponent fejler, den tilfældige variabel er "komponenter, der fejler inden 25 timer", og dens værdi er y = 1. Ved at erstatte i sandsynlighedsfunktionen:
Spørgsmålet er imidlertid, hvor sandsynligt de er for at mislykkes mindre end to komponenter i 50 timer, ikke at nøjagtigt 2 komponenter fejler i 50 timer, derfor skal vi tilføje sandsynlighederne for, at:
-Ingen fejler
-Kun ikke 1
P (mindre end 2 komponenter fejler) = P (0) + P (1)
P (mindre end 2 komponenter fejler) = 0,0183 + 0,0732 = 0.0915
c) At de fejler i det mindste 3 komponenter på 125 timer, betyder at 3, 4, 5 eller mere kan mislykkes på det tidspunkt.
Sandsynligheden for, at det opstår i det mindste en af flere begivenheder er lig med 1 minus sandsynligheden for, at ingen af begivenhederne vil forekomme.
-Den ønskede begivenhed er, at 3 eller flere komponenter fejler på 125 timer
-Hvis begivenheden ikke finder sted, betyder det, at mindre end 3 komponenter fejler, hvis sandsynlighed er: P (0) + P (1) + P (2)
Parameteren μ af fordelingen i dette tilfælde er:
μ = 8 + 2 = 10 fejl på 125 timer.
P (3 eller flere komponenter fejler) = 1- P (0) - P (1) - P (2) =
Endnu ingen kommentarer