Generel ligning af en linje, hvis hældning er lig med 2/3

Den generelle ligning af en linje L er følgende: Ax + By + C = 0, hvor A, B og C er konstanter, x er den uafhængige variabel og og den afhængige variabel.

Hældningen på en linje, generelt betegnet med bogstavet m, der passerer gennem punkterne P = (x1, y1) og Q = (x0, y0) er følgende kvotient m: = (y1-y0) / (x1 -x0 ).

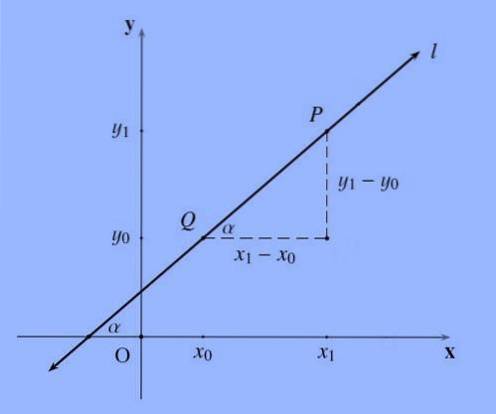
Hældningen på en linje repræsenterer på en bestemt måde hældningen; Mere formelt er hældningen på en linje tangenten for den vinkel, den danner med X-aksen..

Det skal bemærkes, at rækkefølgen, som punkterne er navngivet, er ligeglad, da (y0-y1) / (x0-x1) = - (y1-y0) / (- (x1-x0)) = (y1-y0) / (x1-x0).

Hældning af en linje

Hvis der kendes to punkter, gennem hvilke en linje passerer, er det let at beregne dens hældning. Men hvad hvis disse punkter ikke er kendt?

I betragtning af den generelle ligning for en linje Ax + By + C = 0 er dens hældning m = -A / B.

Hvad er den generelle ligning for en linje, hvis hældning er 2/3?

Da hældningen på linjen er 2/3, etableres ligestillingen -A / B = 2/3, hvormed vi kan se, at A = -2 og B = 3. Så den generelle ligning for en linje med hældning lig med 2/3 er -2x + 3y + C = 0.

Det skal præciseres, at hvis A = 2 og B = -3 vælges, opnås den samme ligning. Faktisk er 2x-3y + C = 0, hvilket er lig med det foregående ganget med -1. Tegnet på C betyder ikke noget, da det er en generel konstant.

En anden observation, der kan foretages, er, at for A = -4 og B = 6 opnås den samme linje, på trods af at deres generelle ligning er forskellig. I dette tilfælde er den generelle ligning -4x + 6y + C = 0.

Er der andre måder at finde linjens generelle ligning på?

Svaret er ja. Hvis hældningen på en linje er kendt, er der foruden den foregående to måder at finde den generelle ligning.

Til dette anvendes Point-Slope-ligningen og Shear-Slope-ligningen..

-Point-Slope-ligningen: Hvis m er hældningen på en linje og P = (x0, y0) et punkt, gennem hvilken den passerer, kaldes ligningen y-y0 = m (x-x0) Point-Slope-ligningen.

-Shear-Slope-ligningen: hvis m er hældningen på en linje, og (0, b) er linjens afskæring med Y-aksen, kaldes ligningen y = mx + b Shear-Slope-ligningen.

Ved hjælp af det første tilfælde opnås det, at Point-Slope-ligningen for en linje, hvis hældning er 2/3, gives ved udtrykket y-y0 = (2/3) (x-x0).

For at nå frem til den generelle ligning skal du gange med 3 på begge sider, og alle vilkår er grupperet på den ene side af ligningen, hvormed det opnås, at -2x + 3y + (2 × 0-3y0) = 0 er den generelle ligning af linjen, hvor C = 2 × 0-3y0.

Hvis det andet tilfælde anvendes, opnås det, at ligningen Cut-Slope for en linje, hvis hældning er 2/3, er y = (2/3) x + b.

Igen multipliceres med 3 på begge sider og grupperer alle variablerne, får vi -2x + 3y-3b = 0. Sidstnævnte er den generelle ligning af linjen, hvor C = -3b.

Når man ser nøje på begge tilfælde, kan det faktisk ses, at det andet tilfælde simpelthen er et bestemt tilfælde af det første (når x0 = 0).

Referencer

1. Fleming, W., & Varberg, D. E. (1989). Præcalculus matematik. Prentice Hall PTR.
2. Fleming, W., & Varberg, D. E. (1989). Precalculus matematik: en problemløsningstilgang (2, Illustreret udgave). Michigan: Prentice Hall.
3. Kishan, H. (2005). Integreret beregning. Atlantic Publishers & Distributors.
4. Larson, R. (2010). Precalculus (8. udgave). Cengage læring.
5. Leal, J. M., og Viloria, N. G. (2005). Flyanalytisk geometri. Mérida - Venezuela: Redaktionel Venezolana C. A.
6. Pérez, C. D. (2006). Forberegning. Pearson Uddannelse.
7. Saenz, J. (2005). Differentiel beregning med tidlige transcendente funktioner til videnskab og teknik (Anden udgave udgave). Hypotenus.
8. Sullivan, M. (1997). Forberegning. Pearson Uddannelse.