
Eneagon egenskaber, hvordan man laver en eneagon, eksempler

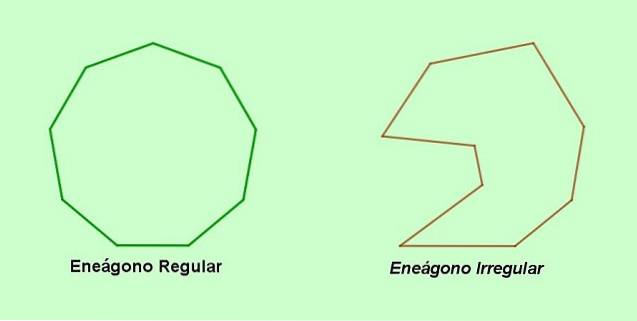
EN eneagon er en polygon med ni sider og ni hjørner, som måske eller ikke kan være regelmæssige. Navnet eneágono kommer fra græsk og består af de græske ord ennea (ni og gonon (vinkel).
Et alternativt navn til den ni-sidede polygon er nonagon, et ord der kommer fra latin nonus (ni og gonon (toppunkt). På den anden side, hvis enegonens sider eller vinkler er ulige med hinanden, så har vi en uregelmæssig enegon. Hvis derimod de ni sider og de ni vinkler på enegonen er ens, er det en regelmæssig enegon.
Artikelindeks
- 1 Egenskaber for enegon
- 1.1 Regelmæssig enegon
- 1.2 Område af enegon kendt side og apotem
- 1.3 Område for en kendt enegon på siden
- 1.4 Omkredsen af den almindelige enegon kendte sin side
- 1.5 Enegonens omkreds kendte sin radius
- 2 Hvordan man laver en regelmæssig eneagon
- 3 eksempler
- 3.1 Eksempel 1
- 3.2 Eksempel 2
- 4 Referencer
Eneagon egenskaber
For en polygon med n sider er summen af dens indvendige vinkler:
(n - 2) * 180º
I enegonen ville det være n = 9, så summen af dens indre vinkler er:
Sa = (9 - 2) * 180º = 7 * 180º = 1260º
I enhver polygon er antallet af diagonaler:
D = n (n - 3) / 2 og i tilfælde af enegon, da n = 9, har vi så D = 27.
Regelmæssig enegon
I den almindelige eneagon eller nonagon er der ni (9) indre vinkler med lige mål, derfor måler hver vinkel en niendedel af den samlede sum af de interne vinkler.
Målingen på en enegons indre vinkler er derefter 1260º / 9 = 140º.
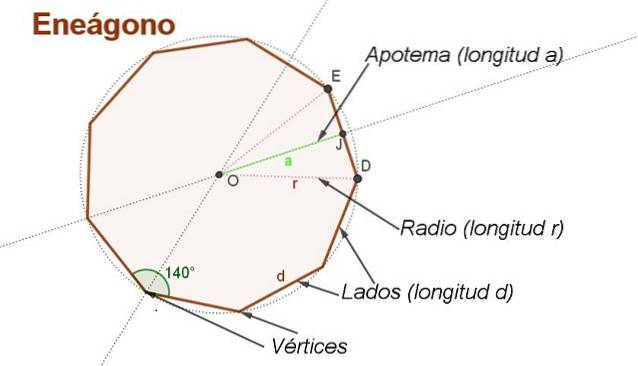
At udlede formlen for området med en regelmæssig enegon med side d det er praktisk at lave nogle hjælpekonstruktioner som dem, der er vist i figur 2.
Centret er placeret ELLER sporing af halveringerne på to tilstødende sider. Centret ELLER lige langt fra hjørner.
En længderadie r er det segment, der går fra midten ELLER til en toppunkt i enegonen. Radierne er vist i figur 2. OD Y OE længde r.
Apotemet er det segment, der går fra midten til midtpunktet på den ene side af enegonen. For eksempel EFT er et apotem, hvis længde er til.
Område af en kendt enegon side og apotem
Vi betragter trekanten ODE i figur 2. Arealet af denne trekant er produktet af dens base FRA for højden EFT divideret med 2:
Areal ODE = (DE * EUT) / 2 = (d * a) / 2
Da der er 9 trekanter med lige areal i enegonen, konkluderes det, at det samme areal er:
Eneagon-området = (9/2) (d * a)
Område af en kendt enegon på siden
Hvis kun længden d af siderne af enegonen er kendt, er det nødvendigt at finde længden af apotemet for at kunne anvende formlen fra det foregående afsnit.
Vi betragter trekanten ØJE rektangel i J (se figur 2). Hvis det tangentielle trigonometriske forhold anvendes, opnår vi:
så(∡OEJ) = EFT / Eks.
Vinklen ∡OEJ = 140º / 2 = 70º, at være EO halvering af enegonens indvendige vinkel.
På den anden side, EFT er længden apotem til.
Så som J er midtpunktet for ED Den følger det EJ = d / 2.
Udskiftning af de tidligere værdier i den tangentrelation, vi har:
tan (70º) = a / (d / 2).
Nu rydder vi apotemets længde:
a = (d / 2) tan (70º).
Det forrige resultat er erstattet i områdeformlen for at opnå:
Eneagon-området = (9/2) (d * a) = (9/2)( d * (d / 2) brunbrun (70º)
Endelig finder vi den formel, der tillader opnåelse af området for den regulære enegon, hvis kun længden er kendt d fra siderne:
Eneagon-området = (9/4) dto tan (70º) = 6.1818 dto
Perimeter af regelmæssig enegon kendte sin side
En polygons omkreds er summen af dens sider. I tilfælde af enegon, da hver og en af siderne måler en længde d, dens omkreds er summen af ni gange d, nemlig:
Perimeter = 9 d
Enegonens omkreds kendte sin radius
I betragtning af trekanten ØJE rektangel i J (se figur 2), anvendes det trigonometriske cosinusforhold:
cos (∡OEJ) = Eks / OE = (d / 2) / r
Hvor fås det fra:
d = 2r cos (70º)
Ved at erstatte dette resultat opnår vi formlen for omkredsen som en funktion af enegonens radius:
Omkreds = 9 d = 18 r cos (70º) = 6.1564 r
Hvordan man laver en regelmæssig eneagon
1- For at bygge en regelmæssig eneagon med en lineal og et kompas skal du starte fra omkredsen c der afgrænser enegonen. (se figur 3)
2- To vinkelrette linjer trækkes gennem centrum O af omkredsen. Derefter markeres krydset A og B på en af linjerne med omkredsen.
3- Med kompasset, centreret i skæringspunktet B og åbningen lig med radius BO, tegnes en bue, der opfanger den oprindelige omkreds ved et punkt C.
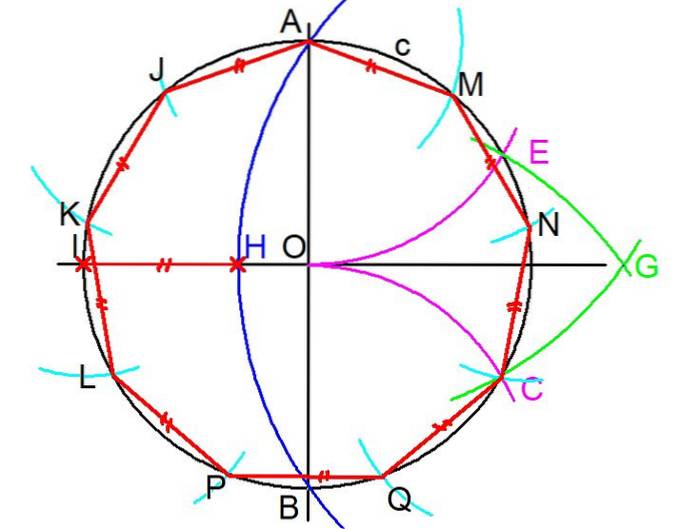
4- Det forrige trin gentages, men når der oprettes et centrum ved A og radius AO, tegnes en bue, der opfanger omkredsen c i punkt E.
5- Med åbning AC og center i A tegnes en omkredsbue. Tilsvarende med åbning BE og centrum B tegnes en anden bue. Skæringspunktet mellem disse to buer er markeret som punkt G.
6- Centrering ved G og åbning GA tegnes en bue, der skærer den sekundære akse (vandret i dette tilfælde) ved punkt H. Skæringspunktet mellem sekundæraksen og den oprindelige omkreds c er markeret som I.
7- Længden af segmentet IH er lig med længden d af siden af enegonen.
8- Med kompasåbning IH = d tegnes buerne i centrum A radius AJ, center J radius AK, center K radius KL og center L radius LP successivt.
9- På samme måde, startende fra A og fra højre side, tegnes buer med radius IH = d, der markerer punkterne M, N, C og Q på den oprindelige omkreds c.
10- Endelig tegnes segmenterne AJ, JK, KL, LP, AM, MN, NC, CQ og endelig PB.
Det skal bemærkes, at konstruktionsmetoden ikke er helt nøjagtig, da det kan verificeres, at den sidste side PB er 0,7% længere end de andre sider. Til dato er der ingen kendt konstruktionsmetode med en lineal og kompas, der er 100% nøjagtig..
Eksempler
Her er nogle bearbejdede eksempler.
Eksempel 1
Du vil bygge en regelmæssig enegon, hvis sider måler 2 cm. Hvilken radius skal have den omkreds, der omgiver den, så når man anvender den tidligere beskrevne konstruktion, opnås det ønskede resultat?
Opløsning:
I et tidligere afsnit blev formlen, der relaterer radius r for den omskrevne cirkel med siden d af en regelmæssig enegon, udledt:
d = 2r cos (70º)
Løsning for r fra det foregående udtryk har vi:
r = d / (2 cos (70º)) = 1,4619 * d
Ved at erstatte værdien d = 2 cm i den foregående formel opnås en radius r på 2,92 cm.
Eksempel 2
Hvad er arealet af en almindelig enegon med en side på 2 cm?
Opløsning:
For at besvare dette spørgsmål skal vi henvise til den tidligere viste formel, der giver os mulighed for at finde området for en kendt enegon i længden d af dens side:
Eneagon-området = (9/4) dto tan (70º) = 6.1818 dto
Ved at erstatte d for dens værdi på 2 cm i den foregående formel får vi:
Eneagon-området = 24,72 cm
Referencer
- C. E. A. (2003). Geometrielementer: med kompasets øvelser og geometri. University of Medellin.
- Campos, F., Cerecedo, F. J. (2014). Matematik 2. Grupo Editorial Patria.
- Freed, K. (2007). Opdag polygoner. Benchmark Education Company.
- Hendrik, V. (2013). Generelle polygoner. Birkhäuser.
- IGER. (s.f.). Matematik Første semester Tacaná. IGER.
- Jr. geometri. (2014). Polygoner. Lulu Press, Inc..
- Miller, Heeren & Hornsby. (2006). Mathematics: Reasoning And Applications (Tiende udgave). Pearson Uddannelse.
- Patiño, M. (2006). Matematik 5. Redaktionel Progreso.


Endnu ingen kommentarer