I mekanik er et objekt i ustabil balance når den ved en let forskydning fra sin position ved hjælp af en kraft ikke vender tilbage til den. For eksempel er kuglen i den følgende figur, når den er over højen, i ustabil ligevægt, da den mindste forstyrrelse får den til at rulle ned ad bakke uden mulighed for at vende tilbage på egen hånd.
I modsætning hertil siges det at når bolden er på en plan overflade, som i midterpositionen ligegyldig balance eller neutral. En forstyrrende kraft kan påføres ved at flytte den til den ene eller den anden side, men hvis kraften forsvinder, bliver bolden stabil igen.
Endelig til højre er bolden i bunden af en konkav beholder. Denne position er også af balance, men af stabil ligevægt. En kraft, der forstyrrer bolden, vil kun få den til at svinge sig lidt omkring den oprindelige position for at ende med at vende stille tilbage til den..
Artikelindeks
Almindelige genstande (og mennesker og dyr) mister deres balance og falder på grund af drejningsmomentet forårsaget af vægten, den kraft, som Jorden udøver på alle genstande i nærheden af overfladen. Når du har en udvidet krop, kaldes det punkt, hvor vægten virker tyngdepunkt.
Vægten kan afbalanceres takket være en støtte, som den, der tilvejebringes af en overflade, og på denne måde bevæger objektet sig ikke. Men alligevel har det stadig muligheden for at dreje et eller andet punkt, for i de udvidede objekter er balancen mellem kræfterne ikke den eneste faktor, der holder dem stille, men også det sted, hvor disse kræfter påføres..
Nedenfor er en figur med en blyant afbalanceret på spidsen, i ustabil balance. Ethvert luftudkast får den til at vælte, men i mellemtiden opvejer vægten og den normale støttekraft hinanden. Derudover har begge kræfter samme handlingslinje, og dette passerer gennem blyantspidsen og sikrer balance..
Men hvis blyanten kun vippes en smule, som vist til højre, stopper vægtens handlingslinje gennem spidsen, som fungerer som en drejning. Derefter producerer vægten ubalanceret drejningsmoment, og pennen roterer med uret..
Stabil ligevægt søges næsten altid, da ustabil ligevægt er, som navnet antyder, ret usikker. Fortsat med eksemplet med blyanten, når den først falder og hviler vandret på overfladen, er den nye position meget mere stabil, end når den stod på spidsen..
Dette skyldes, at tyngdepunktet på den ene side er tættere på overfladen, og på den anden side er blyantens støtteflade meget større..
Når støtteoverfladen er større, er det mere sandsynligt, at normal er i stand til at modvirke vægten, da overfladen er præcis, hvad den normale udøver. Og hvis afstanden fra tyngdepunktet til overfladen er mindre, er vægtstangens arm mindre, og derfor er momentet også mindre..
Afslutningsvis: jo større objektets støttebase er, og jo tættere dens tyngdepunkt på jorden er, jo lavere er sandsynligheden for at vælte, og ligevægten har tendens til at være stabil. Babyer ved dette, og det er derfor, de har tendens til at kravle først, før de risikerer at stå op.
Og hvis legemet er ophængt fra et punkt i stedet for at blive understøttet, spiller tyngdepunktets placering også en fremtrædende rolle, når man skaber balance, som det vil ses kort i de følgende eksempler.
Ligevægten i understøttede kroppe afhænger som sagt af:
-Hvor tæt tyngdepunktet er på overfladen.
-Størrelsen på objektets base.
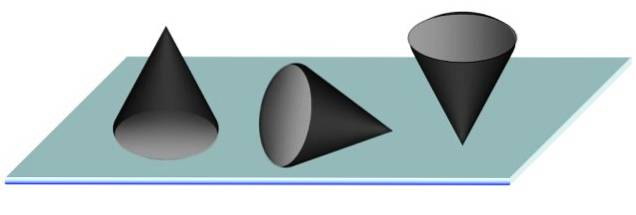
Overvej en kegle på et fladt bord. Den mest stabile position er uden tvivl med bunden af keglen fuldt understøttet på bordet. Dette er den stabile ligevægtsposition, da keglens tyngdepunkt ligger på symmetriaksen og tættere på dens base end til spidsen..
Den ligegyldige ligevægt opnås ved at placere keglen liggende og den ustabile ligevægt svarer til keglen på dens spids, som blyanten, hvilket måske ikke er en let opgave, da keglen ved den mindste bevægelse vælter.
Det er almindeligt at finde ophængte kroppe, der hænger fra mindst et punkt, såsom malerier og lamper. Når du skaber balance, skal du overveje placeringen af tyngdepunktet og ophængningspunktet..
Situationen er let at visualisere ved hjælp af et rektangulært papark eller en regel af homogent materiale. Her falder tyngdepunktet sammen med figurens geometriske centrum, idet det antages, at genstandens masse er jævnt fordelt.
For at placere arket i ustabil ligevægt, er det suspenderet fra et punkt, der er under i tyngdepunktet kan du endda holde arket løst mellem dine fingre for at give dig bevægelsesfrihed.
En lille kraft er tilstrækkelig til, at klingen roterer med det samme i den ene eller den anden retning. Årsagen til drejning er den samme som i tilfældet med det understøttede objekt: vægten udøver et ukompenseret drejningsmoment, der letter rotation af kroppen.
Når det roterer, passerer arket gennem en position, der har en stabil ligevægt, hvor ophængningspunktet er ovenfra tyngdepunkt. Omkring denne position svinger den lidt og stopper endelig.
Hvis en kraft påføres igen, svinger bladet igen, men vender tilbage til den position, hvor ophængningspunktet og tyngdepunktet er justeret med det lodrette.
Endelig kontrolleres den ligegyldige balance ved at føre en pin lige gennem tyngdepunktet. Hvis arket roteres for at være i forskellige positioner, ses det, at der ikke vil være nogen større forskel mellem dem.
Afslutningsvis for organer, der er suspenderet i ustabil ligevægt, er ophængningspunktet under tyngdepunktet. Og det modsatte for stabil ligevægt.
Endnu ingen kommentarer