
Delvise brøker Tilfælde og eksempler
Det delvise fraktioner er fraktioner dannet af polynomer, hvor nævneren kan være et lineært eller kvadratisk polynom, og derudover kan det hæves til en vis styrke. Nogle gange, når vi har rationelle funktioner, er det meget nyttigt at omskrive denne funktion som en sum af delvise eller enkle brøker..
Dette skyldes, at vi på denne måde kan manipulere disse funktioner på en bedre måde, især i tilfælde, hvor det er nødvendigt at integrere nævnte applikation. En rationel funktion er simpelthen kvotienten mellem to polynomer, og de kan være korrekte eller ukorrekte.

Hvis graden af tællerens polynom er mindre end nævneren, kaldes det en rationel korrekt funktion; ellers er det kendt som en forkert rationel funktion.
Artikelindeks
- 1 Definition
- 2 sager
- 2.1 Sag 1
- 2.2 Sag 2
- 2.3 Sag 3
- 2.4 Sag 4
- 3 applikationer
- 3.1 Integreret beregning
- 3.2 Lov om masseaktion
- 3.3 Differentialligninger: logistisk ligning
- 4 Referencer
Definition
Når vi har en forkert rationel funktion, kan vi dele tællerens polynom med nævnerenes polynom og således omskrive brøken p (x) / q (x) efter divisionsalgoritmen som t (x) + s (x ) / q (x), hvor t (x) er et polynom og s (x) / q (x) er en korrekt rationel funktion.
En delvis brøkdel er en hvilken som helst korrekt funktion af polynomer, hvis nævner har formen (ax + b)n o (øksto+ bx + c)n, hvis den polynomiske økseto + bx + c har ikke rigtige rødder, og n er et naturligt tal.
For at omskrive en rationel funktion i delvise fraktioner er den første ting at gøre faktor nævneren q (x) som et produkt af lineære og / eller kvadratiske faktorer. Når dette er gjort, fortsætter vi med at bestemme de delvise fraktioner, som afhænger af arten af disse faktorer..
Sager
Vi overvejer flere sager hver for sig.
Sag 1
Faktorerne for q (x) er alle lineære og ingen gentages. Nemlig:
q (x) = (a1x + b1) (tiltox + bto)… (tilsx + bs)
Der er ingen lineær faktor identisk med en anden. Når denne sag opstår, skriver vi:
p (x) / q (x) = A1/(til1x + b1) + A.to/(tiltox + bto)… + As/(tilsx + bs).
Hvorhen1,TILto,… ,TILs er de konstanter, du vil finde.
Eksempel
Vi ønsker at nedbryde den rationelle funktion i enkle brøker:
(x - 1) / (x3+3xto+2x)
Vi fortsætter med at faktor nævneren, det vil sige:
x3 + 3xto + 2x = x (x + 1) (x + 2)
Senere:
(x - 1) / (x3+3xto+2x) = (x - 1) / x (x + 1) (x + 2)
(x - 1) / x (x + 1) (x + 2) = A / x + B / (x + 1) + C / (x + 2)
Ved anvendelse af mindst almindelige multiple kan det opnås, at:
x - 1 = A (x + 1) (x + 2) + B (x + 2) x + C (x + 1) x.
Vi ønsker at opnå værdierne for konstanterne A, B og C, som kan findes ved at erstatte rødderne, der annullerer hvert af udtrykkene. Ved at erstatte 0 med x har vi:
0 - 1 = A (0 + 1) (0 + 2) + B (0 + 2) 0 + C (0 + 1) 0.
- 1 = 2A
A = - 1/2.
Udskiftning - 1 for x har vi:
- 1 - 1 = A (- 1 + 1) (- 1 + 2) + B (- 1 + 2) (- 1) + C (- 1 + 1) (- 1).
- 2 = - B
B = 2.
Udskiftning - 2 for x har vi:
- 2 - 1 = A (- 2 + 1) (- 2 + 2) + B (- 2 + 2) (- 2) + C (- 2 + 1) (- 2).
-3 = 2C
C = -3/2.
På denne måde opnås værdierne A = -1/2, B = 2 og C = -3/2.
Der er en anden metode til at opnå værdierne A, B og C. Hvis på højre side af ligningen x - 1 = A (x + 1) (x + 2) + B (x + 2) x + C (x + 1) x vi kombinerer termer, vi har:
x - 1 = (A + B + C) xto + (3A + 2B + C) x + 2A.
Da dette er ligestilling med polynomer, har vi, at koefficienterne på venstre side skal være lig med dem på højre side. Dette resulterer i følgende ligningssystem:
A + B + C = 0
3A + 2B + C = 1
2A = - 1
Løsning af dette ligningssystem opnår vi resultaterne A = -1/2, B = 2 og C = -3/2.
Endelig har vi erstattet de opnåede værdier, at:
(x - 1) / x (x + 1) (x + 2) = - 1 / (2x) + 2 / (x + 1) - 3 / (2 (x + 2)).
Sag 2
Faktorerne for q (x) er alle lineære, og nogle gentages. Antag at (ax + b) er en faktor, der gentager “s” gange; derefter svarer denne faktor til summen af "s" delfraktioner.
TILs/ (økse + b)s + TILs-1/ (økse + b)s-1 +… + A1/ (økse + b).
Hvor As,TILs-1,… , TIL1 er konstanterne, der skal bestemmes. Med det følgende eksempel viser vi, hvordan man bestemmer disse konstanter.
Eksempel
Nedbrydes i delvise fraktioner:
(x - 1) / (xto(x - 2)3)
Vi skriver den rationelle funktion som en sum af delfraktioner som følger:
(x - 1) / (xto(x - 2)3) = A / xto + B / x + C / (x - 2)3 + D / (x - 2)to + E / (x - 2).
Senere:
x - 1 = A (x - 2)3 + B (x - 2)3x + Cxto + D (x - 2) xto + E (x - 2)toxto
Ved at erstatte 2 med x har vi det:
7 = 4C, dvs. C = 7/4.
Ved at erstatte 0 med x har vi:
- 1 = -8A eller A = 1/8.
Ved at erstatte disse værdier i den foregående ligning og udvikle har vi det:
x - 1 = 1/8 (x3 - 6xto + 12x - 8) + Bx (x3 - 6xto + 12x - 8) + 7 / 4xto +Dx3 - 2Dxto + Tidligereto(xto - 4x + 4)
x - 1 = (B + E) x4 + (1/8 - 6B + D - 4E) x3 + (- ¾ + 12B + 7/4 - 2D + 4E) xto +(3/2 - 8B) x - 1.
Ved ligningskoefficienter opnår vi følgende ligningssystem:
B + E = 0;
1 / 8-6B + D-4E = 1;
- 3/4 + 12B + 7/4 - 2D + 4E = 0
3/2 - 8B = 0.
Løsning af systemet har vi:
B = 3/16; D = 5/4; E = - 3/16.
Til dette er vi nødt til at:
(x - 1) / (xto(x - 2)3) = (1/8) / xto + (3/16) / x + (7/4) / (x - 2)3 + (5/4) / (x - 2)to - (3/16) / (x - 2).
Sag 3
Faktorerne for q (x) er lineære kvadratiske uden nogen gentagne kvadratiske faktorer. I dette tilfælde er den kvadratiske faktor (axto + bx + c) svarer til den delvise brøk (Ax + B) / (axto + bx + c), hvor konstanterne A og B er dem, vi vil bestemme.
Følgende eksempel viser, hvordan man fortsætter i dette tilfælde
Eksempel
Nedbrydes i enkle fraktioner a (x + 1) / (x3 - 1).
Først fortsætter vi med at faktorere nævneren, hvilket giver os som et resultat:
(x - 1) = (x - 1) (x + x +1).
Vi kan observere det (xto + x + 1) er et irreducerbart kvadratisk polynom; det vil sige, det har ikke rigtige rødder. Dets nedbrydning i delvise fraktioner vil være som følger:
(x + 1) / (x - 1) (xto + x +1) = A / (x - 1) + (Bx + C) / (xto + x +1)
Fra dette opnår vi følgende ligning:
x + 1 = (A + B) xto +(A - B + C) x + (A - C)
Ved hjælp af ligestilling af polynomer opnår vi følgende system:
A + B = 0;
AB + C = 1;
AC = 1;
Fra dette system har vi, at A = 2/3, B = - 2/3 og C = 1/3. Udskiftning har vi det:
(x + 1) / (x - 1) (xto + x +1) = 2/3 (x - 1) - (2x + 1) / 3 (xto + x +1).
Sag 4
Endelig er tilfælde 4 den, hvor faktorerne i q (x) er lineære og kvadratiske, hvor nogle af de lineære kvadratiske faktorer gentages.
I dette tilfælde, hvis (axto + bx + c) er en kvadratisk faktor, der gentager “s” gange, så den delvise brøk svarende til faktoren (axto + bx + c) vil være:
(TIL1x + B) / (axto + bx + c) + ... + (As-1x + Bs-1) / (axto + bx + c)s-1 + (TILsx + Bs) / (axto + bx + c)s
Hvor As, TILs-1,…, A og Bs, Bs-1,..., B er konstanterne, der skal bestemmes.
Eksempel
Vi ønsker at nedbryde følgende rationelle funktion i delvise brøker:
(x - 2) / (x (xto - 4x + 5)to)
Som xto - 4x + 5 er en irreducerbar kvadratisk faktor, vi har, at dens nedbrydning i delvise fraktioner er givet ved:
(x - 2) / (x (xto - 4x + 5)to) = A / x + (Bx + C) / (xto - 4x +5) + (Dx + E) / (xto - 4x + 5)to
Forenkling og udvikling har vi tilbage med:
x - 2 = A (xto - 4x + 5)to + (Bx + C) (xto - 4x + 5) x + (Dx + E) x
x - 2 = (A + B) x4 + (- 8A - 4B + C) x3 + (26A + 5B - 4C + D) xto + (- 40A + 5C + E) x + 25A.
Fra ovenstående har vi følgende ligningssystem:
A + B = 0;
- 8A - 4B + C = 0;
26A + 5B - 4C + D = 0;
- 40A + 5C + E = 1;
25A = 2.
Når vi løser systemet, er vi tilbage med:
A = - 2/25, B = 2/25, C = - 8/25, D = 2/5 og E = - 3/5.
Ved at erstatte de opnåede værdier har vi:
(x - 2) / (x (xto - 4x + 5)to) = -2 / 25x + (2x - 8) / 25 (xto - 4x +5) + (2x - 3) / 5 (xto - 4x + 5)to
Ansøgninger
Integreret beregning
Delvise fraktioner anvendes primært til undersøgelse af integreret beregning. Dernæst vil vi se nogle eksempler på, hvordan man udfører integraler ved hjælp af delvise brøker.
Eksempel 1
Vi ønsker at beregne integralet af:
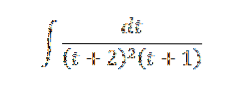
Vi kan se, at nævneren q (x) = (t + 2)to(t + 1) består af lineære faktorer, hvor en af disse gentages; det er derfor, vi er i tilfælde 2.
Vi skal:
1 / (t + 2)to(t + 1) = A / (t + 2)to +B / (t + 2) + C / (t + 1)
Vi omskriver ligningen, og vi har:
1 = A (t + 1) + B (t + 2) (t + 1) + C (t + 2)to
Hvis t = - 1, har vi:
1 = A (0) + B (1) (0) + C (1)
1 = C
Hvis t = - 2, giver det os:
1 = A (- 1) + B (0) (- 1) + C (0)
A = - 1
Så hvis t = 0:
1 = A (1) + B (2) (1) + C (2)
Erstatning af værdierne for A og C:
1 = - 1 + 2B + 4
1 = 3 + 2B
2B = - 2
Fra ovenstående har vi, at B = - 1.
Vi omskriver integralet som:
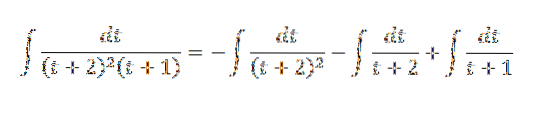
Vi fortsætter med at løse det ved substitutionsmetoden:
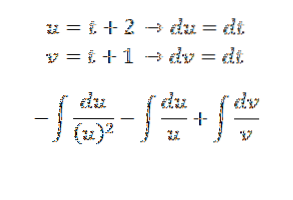
Dette er resultatet:
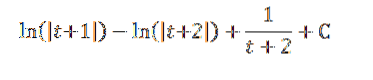
Eksempel 2
Løs følgende integral:

I dette tilfælde kan vi faktorere til q (x) = xto - 4 som q (x) = (x - 2) (x + 2). Vi er klart i tilfælde 1. Derfor:
(5x - 2) / (x - 2) (x + 2) = A / (x - 2) + B / (x + 2)
Det kan også udtrykkes som:
5x - 2 = A (x + 2) + B (x - 2)
Hvis x = - 2, har vi:
- 12 = A (0) + B (- 4)
B = 3
Og hvis x = 2:
8 = A (4) + B (0)
A = 2
Således står vi tilbage med at løse den givne integral svarer til at løse:
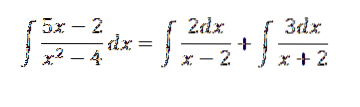
Dette giver os som et resultat:
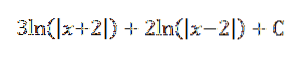
Eksempel 3
Løs integralet:
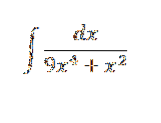
Vi har q (x) = 9x4 + xto , at vi kan faktorere det i q (x) = xto(9xto + 1).
Denne gang har vi en gentagen lineær faktor og en kvadratisk faktor; det vil sige, vi er i tilfælde 3.
Vi skal:
1 / xto(9xto + 1) = A / xto + B / x + (Cx + D) / (9xto + 1)
1 = A (9xto + 1) + Bx (9xto + 1) + Cxto + Dxto
Gruppering og brug af lige polynomer har vi:
1 = (9B + C) x + (9A + D) x + Bx + A
A = 1;
B = 0;
9A + D = 0;
9B + C = 0
Fra dette ligningssystem har vi:
D = - 9 og C = 0
På denne måde har vi:
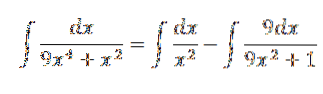
Ved at løse ovenstående har vi:
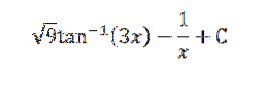
Lov om masseaktion
En interessant anvendelse af de delvise fraktioner, der anvendes på den integrale beregning, findes i kemi, mere præcist i loven om masseaktion.
Antag, at vi har to stoffer, A og B, som forener og danner et stof C, så afledningen af mængden af C med hensyn til tid er proportional med produktet af mængderne A og B til enhver tid.
Vi kan udtrykke loven om masseaktion som følger:
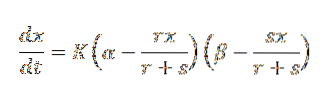
I dette udtryk er α det indledende antal gram svarende til A og β det indledende antal gram svarende til B.
Desuden repræsenterer r og s antallet af henholdsvis A og B, der kombineres for at danne r + s gram C. For sin del repræsenterer x antallet af gram stof C på tidspunktet t, og K er proportionalitetskonstanten . Vi kan omskrive ovenstående ligning som:

Foretag følgende ændring:

Vi har, at ligningen bliver:

Fra dette udtryk kan vi få:
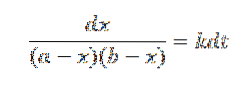
Hvor hvis a ≠ b, kan delfraktioner bruges til integration.
Eksempel
Lad os for eksempel tage et stof C, der opstår ved at kombinere et stof A med et B, på en sådan måde, at masseloven er opfyldt, hvor værdierne for a og b er henholdsvis 8 og 6. Giv en ligning, der giver os værdien af gram C som en funktion af tiden.
Ved at erstatte værdierne i den givne masselov har vi:

Når vi adskiller variabler, har vi:

Her kan 1 / (8 - x) (6 - x) skrives som summen af delbrøker som følger:
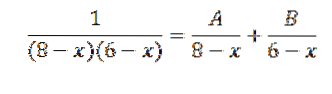
Således er 1 = A (6 - x) + B (8 - x)
Hvis vi erstatter 6 med x, har vi B = 1/2; og ved at erstatte 8 med x, har vi A = - 1/2.
Integration af delbrøker har vi:

Dette giver os som et resultat:

Differentialligninger: logistisk ligning
En anden anvendelse, der kan gives til delvise fraktioner, er i den logistiske differentialligning. I enkle modeller har vi, at væksten i en befolkning er proportional med dens størrelse; nemlig:
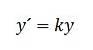
Denne sag er et ideal og betragtes som realistisk, indtil det sker, at de tilgængelige ressourcer i et system er utilstrækkelige til at støtte befolkningen..
I disse situationer er det mest rimelige at tænke, at der er en maksimal kapacitet, som vi vil kalde L, som systemet kan opretholde, og at vækstraten er proportional med størrelsen af befolkningen ganget med den tilgængelige størrelse. Dette argument fører til følgende differentialligning:
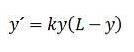
Dette udtryk kaldes den logistiske differentialligning. Det er en adskillelig differentialligning, der kan løses med den delvise fraktionsintegrationsmetode.
Eksempel
Et eksempel ville være at overveje en population, der vokser i henhold til følgende logistiske differentialligning y '= 0,0004y (1000 - y), hvis oprindelige data er 400. Vi ønsker at vide størrelsen af befolkningen på tidspunktet t = 2, hvor t måles i år.
Hvis vi skriver y 'med Leibniz's notation som en funktion, der afhænger af t, har vi:

Integralet på venstre side kan løses ved hjælp af den delvise fraktionsintegrationsmetode:
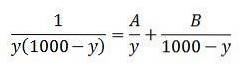
Vi kan omskrive denne sidste ligestilling som følger:
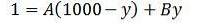
- Ved at erstatte y = 0 har vi, at A er lig med 1/1000.
- Ved at erstatte y = 1000 har vi, at B er lig med 1/1000.
Med disse værdier er integralet som følger:
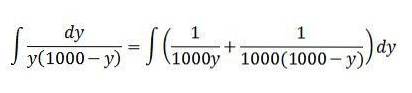
Løsningen er:

Brug af de oprindelige data:

Når du rydder, og vi har:

Så har vi det ved t = 2:
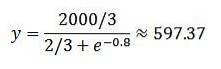
Afslutningsvis er befolkningsstørrelsen efter 2 år cirka 597,37.
Referencer
- A, R. A. (2012). Matematik 1. Andes Universitet. Publikationsrådet.
- Cortez, I. og Sanchez, C. (s.f.). 801 Løst integraler. National Experimental University of Tachira.
- Leithold, L. (1992). Beregningen med analytisk geometri. HARLA, S.A.
- Purcell, E. J., Varberg, D. og Rigdon, S. E. (2007). Beregning. Mexico: Pearson Education.
- Saenz, J. (s.f.). Integreret beregning. Hypotenus.



Endnu ingen kommentarer