Det elastisk kraft er den kraft, som et objekt udøver for at modstå en ændring i dets form. Det manifesterer sig i et objekt, der har tendens til at genvinde sin form, når det er under påvirkning af en deformationskraft.
Den elastiske kraft kaldes også gendannelseskraften, fordi den modsætter sig deformation for at returnere genstande til deres ligevægtsposition. Overførslen af den elastiske kraft sker gennem de partikler, der udgør genstandene.
For eksempel, når en metalfjeder komprimeres, udøves en kraft, der skubber fjederpartiklerne, hvilket mindsker adskillelsen mellem dem, samtidig med at partiklerne modstår at blive skubbet ved at udøve en kraft i modsætning til kompression..
Hvis det i stedet for at komprimere fjederen trækkes, strækkes det, adskilles de partikler, der udgør det. Ligeledes modstår partiklerne adskillelse ved at udøve en kraft, der strider mod strækning..
Objekter, der har den egenskab at genvinde deres oprindelige form, når de modsætter sig deformationskraften, kaldes elastiske genstande. Fjedre, elastikker og bungee snore er eksempler på elastiske genstande..
Artikelindeks
Den elastiske kraft (Fk) er den kraft, som et objekt udøver for at genvinde sin tilstand af naturlig balance efter at være påvirket af en ekstern kraft.
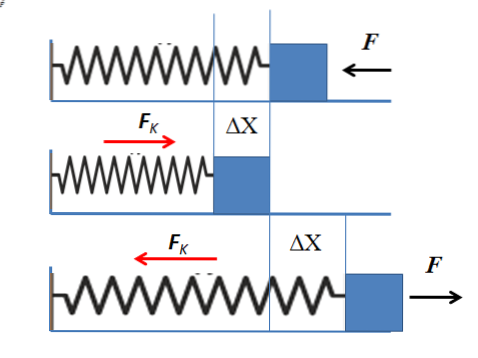
For at analysere den elastiske kraft vil det ideelle fjedermassesystem blive taget i betragtning, som består af en vandret placeret fjeder fastgjort i den ene ende til væggen og i den anden ende til en blok med ubetydelig masse. De andre kræfter, der virker på systemet, såsom friktionskraften eller tyngdekraften, vil ikke blive taget i betragtning..
Hvis der udøves en vandret kraft på massen, rettet mod væggen, overføres den mod fjederen og komprimerer den. Fjederen bevæger sig fra sin ligevægtsposition til en ny position. Da objektet har tendens til at forblive i ligevægt, manifesterer den elastiske kraft i foråret, der modsætter sig den påførte kraft.
Forskydningen angiver, hvor meget fjederen har deformeret, og den elastiske kraft er proportional med forskydningen. Når fjederen er komprimeret, øges variationen i position, og følgelig øges den elastiske kraft..
Jo mere fjederen er komprimeret, jo mere modsatrettede kræfter udøver den, indtil den når et punkt, hvor den påførte kraft og den elastiske kraftbalance, derfor stopper fjedermassesystemet med at bevæge sig. Når du holder op med at anvende kraft, er den eneste kraft, der virker, den elastiske kraft. Denne kraft fremskynder fjederen i den modsatte retning af deformationen, indtil den genvinder ligevægtstilstanden.
Det samme sker, når fjederen strækkes og trækker massen vandret. Fjederen strækkes og udøver straks en kraft, der er proportional med forskydningen mod strækningen.
Den elastiske kraftformel udtrykkes af Hookes lov. Denne lov siger, at den lineære elastiske kraft, der udøves af en genstand, er proportional med forskydningen.
Fk = -k.Δs [1]
Fk = Elastisk kraft
k = Konstant af proportionalitet
Δs = Forskydning
Når objektet forskydes vandret, som i tilfældet med fjederen fastgjort til væggen, er forskydningen Δx, og udtrykket for Hookes lov er skrevet:
Fk = -k.Δx [to]
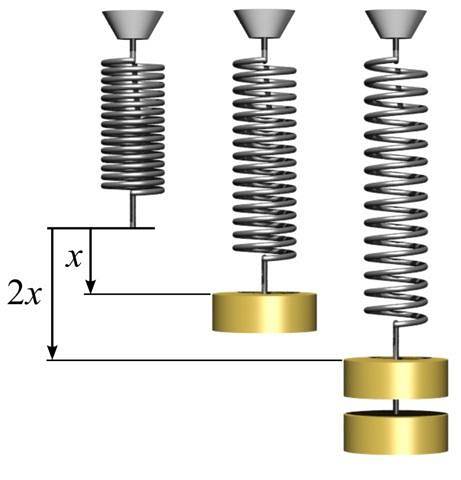
Det negative tegn i ligningen indikerer, at fjederens elastiske kraft er i den modsatte retning af den kraft, der forårsagede forskydningen. Proportionalitetskonstanten k er en konstant, der afhænger af typen af materiale fjederen er lavet af. Enhed af konstanten k det er N / m.
Elastiske objekter har en elasticitetsgrænse, der afhænger af deformationskonstanten. Hvis den strækkes ud over den elastiske grænse, deformeres den permanent.
Ligninger [1] og [2] gælder for små forskydninger af fjederen. Når forskydningerne er større, udtryk med større magt Δx.
Den elastiske kraft virker på fjederen ved at bevæge den mod sin ligevægtsposition. Under denne proces stiger den potentielle energi i fjedermassesystemet. Den potentielle energi på grund af arbejdet udført af den elastiske kraft udtrykkes i ligning [3].
U = ½ k . Δxto[3]
Potentiel energi udtrykkes i Joule (J).
Når deformationskraften ikke længere påføres, accelererer fjederen mod ligevægtspositionen, hvilket mindsker den potentielle energi og øger den kinetiske energi..
Fjedermassesystemets kinetiske energi, når det når ligevægtspositionen, bestemmes af ligning [4].
OGk= ½ m.vto[4]
m = masse
v = fjederhastighed
For at løse fjedermassesystemet anvendes Newtons anden lov under hensyntagen til, at den elastiske kraft er en variabel kraft.
Hvor meget kraft, der er nødvendig for at påføre en fjeder, for at den kan strække sig 5 cm, hvis fjederkonstanten er 35N / m?
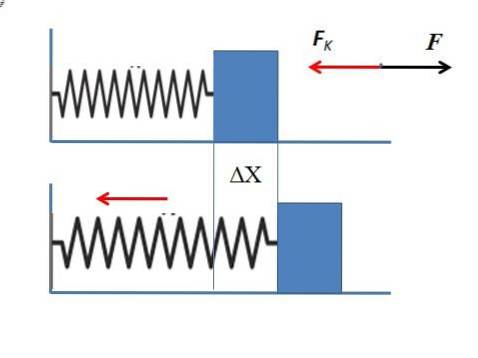
Da påføringskraften er modsat den elastiske kraft, bestemmes den Fk forudsat at fjederen er strakt vandret. Resultatet kræver ikke det negative tegn, da kun anvendelseskraften er nødvendig.
Hookes lov
Fk = -k.Δx
Den konstante k foråret er 35N / m.
Δx = 5 cm = 0,05 m
Fk = -35N / m. 0,05 m
Fk = - 1,75N = - F
Havde brug for 1,75 N kraft til at deformere fjederen 5 cm.
Hvad er belastningskonstanten for en fjeder, der strækkes 20 cm ved handling af en styrke af 60N?
Δx =20 cm = 0,2 m
F = 60N
Fk = -60N = - F
k = - Fk / Δx
= - (- 60N) / 0,2m
k = 300 N / m
Forårskonstanten er 300N / m
Hvad er den potentielle energi, der henvises til arbejdet udført af den elastiske kraft af en kompressionsfjeder 10 cm og dens stamme konstant er 20N / m?
Δx =10 cm = 0,1 m
k = 20 N / m
Fk = -20N / m. 0,1 m
Fk = -200N
Fjederens elastiske kraft er -200N.
Denne kraft fungerer på fjederen for at bevæge den mod sin ligevægtsposition. Hvis du udfører dette arbejde, øges systemets potentielle energi.
Den potentielle energi beregnes med ligningen [3]
U = ½ k . Δxto
U = ½ (20N / m). (0,1 m)to
U = 0.1Joules
Endnu ingen kommentarer