Resulterende kraft, hvordan det beregnes og øvelser løses

Det kraft resulterer det er summen af ​​alle kræfter, der virker på den samme krop. Når et legeme eller et objekt udsættes for virkningen af ​​flere kræfter samtidigt, opstår der en effekt. Aktiveringskræfter kan erstattes af en enkelt kraft, der producerer den samme effekt. Denne enkelte kraft er den resulterende kraft, også kendt som nettokraften, og er repræsenteret af symbolet F_R .

Den effekt, det producerer F_R det vil afhænge af dets størrelse, retning og sans. Fysiske størrelser, der har retning og sans, er vektormængder.

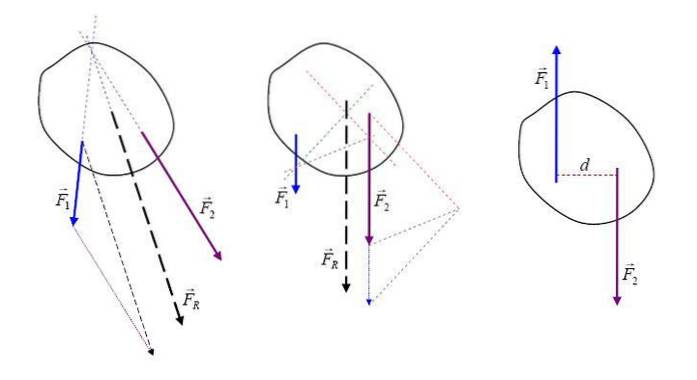
At være de kræfter, der virker på en kropsvektorstørrelse, den resulterende kraft F_R  er en vektorsum af alle kræfter og kan repræsenteres grafisk med en pil, der angiver dens retning og retning.

Med den resulterende kraft forenkles problemet med et legeme, der er påvirket af flere kræfter, ved at reducere det til en enkelt kraft, der virker.

Artikelindeks

• 1 Formel
• 2 Hvordan beregner man den resulterende kraft?
  • 2.1 resulterende af parallelle kræfter 
  • 2.2 Ikke-parallelle kræfter
• 3 Løst øvelser
• 4 Referencer

Formel

Den matematiske repræsentation af den resulterende kraft er en vektorsammensætning af kræfterne.

 F_R= ∑F          (1)

 ∑F = F₁+ F_to+ F₃+... F_N           (to)

F_R= Resulterende kraft

∑F = Summen af ​​styrker

N= Antal styrker

Den resulterende kraft kan også repræsenteres af Newtons anden lovligning.

   F_R= m.til          (3)

m= kropsmasse

a = kropsacceleration

Hvis ligning (1) er substitueret i ligning (3), opnås følgende ligninger:

∑F = m.til          (4)

F₁+ F_to+ F₃+... F_{N =} m.til          (5)

De matematiske udtryk (4) og (5) giver information om kroppens tilstand ved at opnå accelerationsvektoren til.

Hvordan beregner man den resulterende kraft?

Den resulterende styrke opnås ved at anvende Newtons anden lov, der siger følgende:

Nettokraften, der virker på et legeme, er lig med produktet af dets masse og den acceleration, det får. (Ligning (3))

Kroppens acceleration vil have retning af den anvendte nettokraft. Hvis alle de kræfter, der virker på kroppen, er kendt, ville det være tilstrækkeligt at tilføje det vektorisk for at opnå den resulterende kraft. Ligeledes, hvis den resulterende kraft er kendt, ville det være nok at dele den med kroppens masse for at opnå dens acceleration.

Hvis den resulterende kraft er nul, er kroppen i ro eller med konstant hastighed. Hvis en enkelt kraft virker på kroppen, er den resulterende kraft lig med den kraft F_R=F.

Når flere kræfter virker på den samme krop, skal vektorkomponenterne i kraften tages i betragtning, og om disse kræfter er parallelle eller ej.

For eksempel, hvis vi glider en bog vandret på et bord vandret, er kræfterne i vandret retning de eneste, der giver acceleration til kroppen. Den lodrette nettokraft på bogen er nul.

Hvis kraften, der påføres bogen, har en hældning i forhold til bordets vandrette plan, skrives kraften som en funktion af de lodrette og vandrette komponenter.

Resulterer parallelle kræfter 

De parallelle kræfter, der virker på et legeme, er de kræfter, der virker i samme retning. De kan være af to typer af lige eller modsat betydning.

Når de kræfter, der virker på en krop, har samme retning og samme retning eller er i den modsatte retning, opnås den resulterende kraft ved at udføre den algebraiske sum af de numeriske værdier af kræfterne.

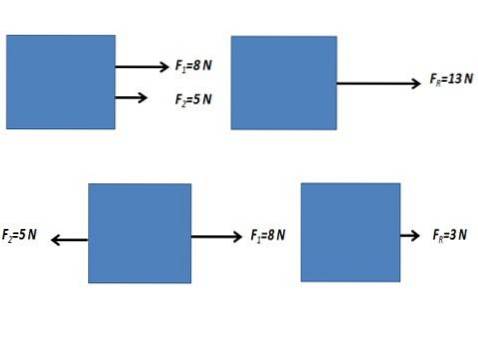
Ikke-parallelle kræfter

Når ikke-parallelle kræfter påføres et legeme, vil den resulterende af kræfterne have rektangulære og lodrette komponenter. Det matematiske udtryk til beregning af nettokraften er:

F_R^to= (∑ F_x)^to+(∑ F_Y)^to            (6)

så θ_x= ∑ F_Y / ∑ F_x         (7)

∑ F_x  og ∑ F_x= Algebraisk opsummering af komponenterne x og Y af anvendte kræfter

θ_x= vinkel dannet af den resulterende kraft F_R med skaft x

Bemærk, at den resulterende udtrykskraft (6) ikke er fremhævet med fed skrift, og det er fordi den kun udtrykker den numeriske værdi. Retningen bestemmes af vinklen θ_x.

Udtryk (6) er gyldigt for kræfter, der virker i samme plan. Når kræfter virker i rummet, tages der hensyn til komponenten z kraft, når der arbejdes med rektangulære komponenter.

Løst øvelser

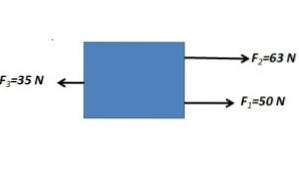
De parallelle kræfter i samme retning tilføjes og trækkes med den parallelle kraft i den modsatte retning

F_R= 63 N + 50 N - 35 N = 78N

Den resulterende kraft har en størrelse på 78N med vandret retning.

2. Beregn den resulterende kraft af et legeme under indflydelse af to kræfter F_{1 Y} F_to. Kraften F₁ den har en størrelse på 70N og påføres vandret. Kraften F_to har en størrelse på 40N og påføres i en vinkel på 30 ° til det vandrette plan.

For at løse denne øvelse tegnes et frit kropsdiagram med koordinatakserne x og Y

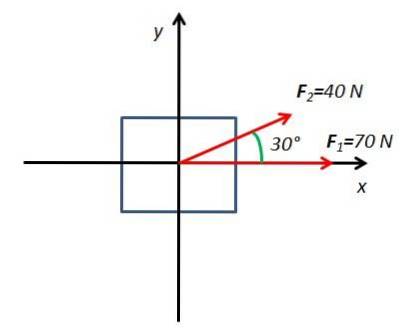
Alle komponenter bestemmes x og Y af de kræfter, der virker på kroppen. Kraften F₁ har kun en vandret komponent på aksen x. Kraften F_to den har to komponenter F_2x  og F_{2 og} som fås fra sinus- og cosinusfunktionerne i vinklen 30 °.

F_1x = F₁=70N

F_2x = F_to cos 30 ° = 40 N.cos 30 ° = 34,64N

F_{1 år} = 0

F_{2 og}= F_to uden 30 ° = 40 uden 30 ° = 20N

∑ F_x =70N + 34,64N = 104,64N

∑ F_Y=20N + 0 = 20N

Når de resulterende kræfter i skaftet er bestemt x og Y vi fortsætter med at opnå den numeriske værdi af den resulterende kraft.

F_R^to= (∑ F_x)^to+(∑ F_Y)^to

Den resulterende kraft er kvadratroden af ​​summen af ​​de kvadrerede komponenter i kræfterne

F_R= √ (104,64N)^to+(20N)^to

F_R= 106,53N

Vinklen dannet af den resulterende kraft F_R er opnået fra følgende udtryk:

θ_x= så^-1(∑ F_Y / ∑ F_x)

θ_x= så^-1(20N / 104,64N) = 10,82 °

Den resulterende kraft F_R har en styrke på 106,53N og har en retning bestemt af vinklen på 10,82 °, som den danner med vandret.

Referencer

1. Dola, G, Duffy, M og Percival, A. Fysik. Spanien: Heinemann, 2003.
2. Avison, J H. Fysikens verden. Indien: Thomas Nelson og sønner, 1989.
3. Pinsent, M. Fysiske processer. Storbritannien: Nelson Thomas, 2002.
4. Yadav, S K. Ingeniørmekanik. Delhi: Discovery Publishing House, 2006.
5. Serway, R A og Jewett, J W. Fysik for forskere og ingeniører. Californien, USA: Brooks / Cole, 2010.