
Injektiv funktion fungerer hvad det er, hvad det er til og eksempler

EN injektionsfunktion er en hvilken som helst relation mellem elementer i domænet og et enkelt element i codomain. Også kendt som funktion en efter en ( elleve ), er en del af klassificeringen af funktioner med hensyn til den måde, deres elementer er relateret på.
Et element i codomain kan kun være billedet af et enkelt element i domænet, på denne måde kan værdierne for den afhængige variabel ikke gentages.
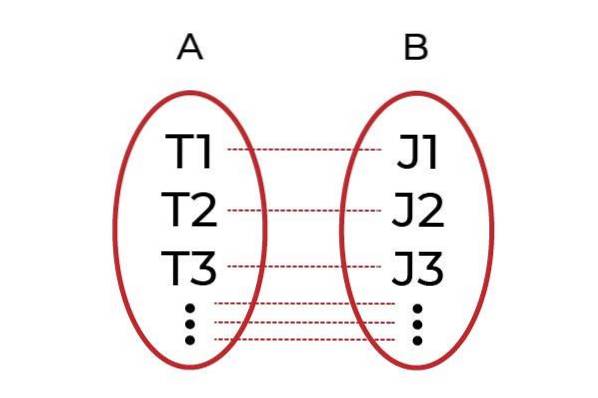
Et klart eksempel ville være at gruppere mænd med job i gruppe A og i gruppe B alle chefer. Funktionen F Det er den, der forbinder hver arbejdstager med sin chef. Hvis hver arbejdstager er tilknyttet en anden chef igennem F, derefter F vil være en injektionsfunktion.
At overveje injektionsmiddel til en funktion skal følgende være opfyldt:
∀ x1 ≠ xto ⇒ F (x1 ) ≠ F (xto )
Dette er den algebraiske måde at sige på For alle x1 forskellig fra xto du har en F (x1 ) forskellig fra F (xto ).
Artikelindeks
- 1 Hvad er injektionsfunktionerne til?
- 1.1 Funktionskonditionering
- 2 Eksempler på injektionsfunktioner med løste øvelser
- 2.1 Eksempel 1
- 2.2 Eksempel 2
- 2.3 Eksempel 3
- 2.4 Eksempel 4
- 2.5 Eksempel 5
- 2.6 Eksempel 6
- 2.7 Eksempel 7
- 3 Øvelser foreslået til klasse / hjem
- 4 Referencer
Hvad er injektionsfunktioner til?
Injektivitet er en egenskab ved kontinuerlige funktioner, da de sikrer tildelingen af billeder til hvert element i domænet, et væsentligt aspekt i en funktions kontinuitet..
Når man tegner en linje parallelt med aksen x på grafen for en injektionsfunktion skal du kun røre ved grafen på et enkelt punkt, uanset højden eller størrelsen af Y linjen er trukket. Dette er den grafiske måde at teste en funktions injektionsevne på.
En anden måde at teste, om en funktion er injektionsmiddel, løser den uafhængige variabel x med hensyn til den afhængige variabel Y. Derefter skal det verificeres, hvis domænet for dette nye udtryk indeholder de reelle tal på samme tid som for hver værdi af Y der er en enkelt værdi af x.
Funktionerne eller ordenforholdene adlyder blandt andet notationen F: DF→CF
Hvad der læses F løber fra DF op til CF
Hvor funktionen F relatere sætene Domæne Y Codomain. Også kendt som startsæt og målsæt.
Dominion DF indeholder de tilladte værdier for den uafhængige variabel. Kodomænet CF Den består af alle de værdier, der er tilgængelige for den afhængige variabel. Elementerne i CF relateret til DF er kendt som Funktionsområde (RF ).
Funktionskonditionering
Nogle gange kan en funktion, der ikke er injektionsdygtig, udsættes for visse betingelser. Disse nye forhold kan gøre det til et injektionsfunktion. Alle former for ændringer af funktionens domæne og codomain er gyldige, hvor målet er at opfylde egenskaberne ved injektivitet i den tilsvarende relation.
Eksempler på injektionsfunktioner med løste øvelser
Eksempel 1
Lad funktionen F: R → R defineret af linjen F (x) = 2x - 3
A: [Alle reelle tal]
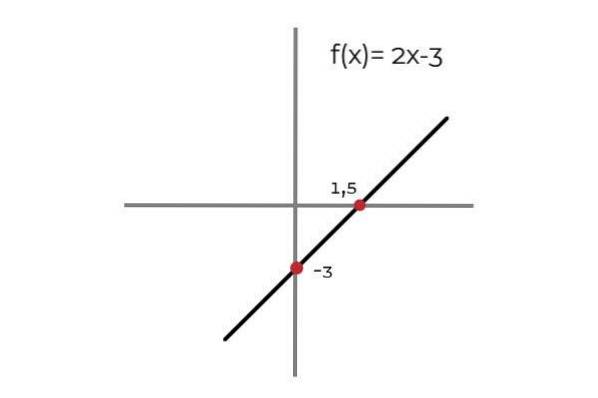
Det bemærkes, at for hver værdi af domænet er der et billede i kodomænet. Dette billede er unikt, hvilket gør F til en injektionsfunktion. Dette gælder for alle lineære funktioner (Funktioner hvis største grad af variablen er en).
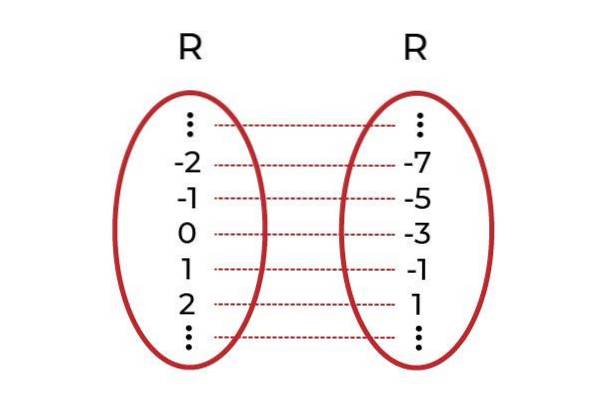
Eksempel 2
Lad funktionen F: R → R defineret af F (x) = xto +1
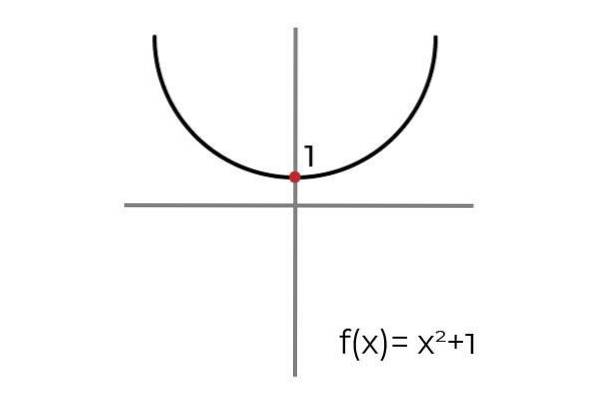
Når man tegner en vandret linje, observeres det, at grafen findes ved mere end en lejlighed. På grund af dette funktionen F det er ikke injektionsdygtigt, så længe det er defineret R → R
Vi fortsætter med at konditionere funktionens domæne:
F: R+ ELLER 0 → R
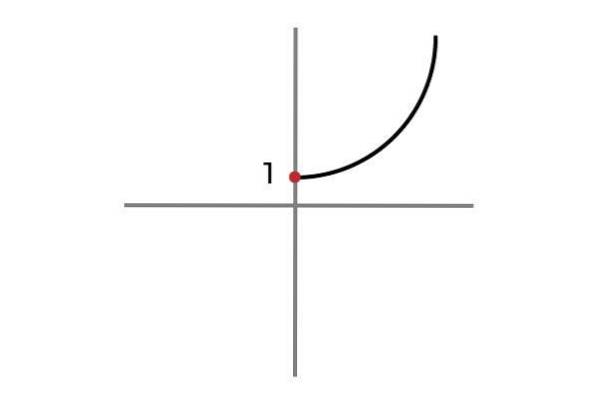
Nu tager den uafhængige variabel ikke negative værdier, på denne måde undgår man gentagne resultater og funktionen F: R+ ELLER 0 → R defineret af F (x) = xto + 1 er injektionsdygtig.
En anden homolog løsning ville være at begrænse domænet til venstre, det vil sige at begrænse funktionen til kun at tage negative og nul værdier.
Vi fortsætter med at konditionere funktionens domæne
F: R- ELLER 0 → R
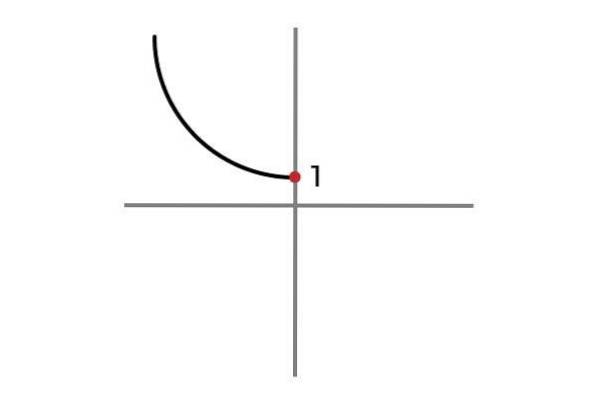
Nu tager den uafhængige variabel ikke negative værdier, på denne måde undgår man gentagne resultater og funktionen F: R- ELLER 0 → R defineret af F (x) = xto + 1 er injektionsdygtig.
Trigonometriske funktioner har adfærd svarende til bølger, hvor det er meget almindeligt at finde gentagelser af værdier i den afhængige variabel. Gennem specifik konditionering, baseret på forudgående kendskab til disse funktioner, kan vi indsnævre domænet for at opfylde betingelserne for injektivitet.
Eksempel 3
Lad funktionen F: [ -π / 2, π / 2 ] → R defineret af F (x) = Cos (x)
I intervallet [ -π / 2 → π / 2 ] cosinusfunktionen varierer dens resultater mellem nul og en.
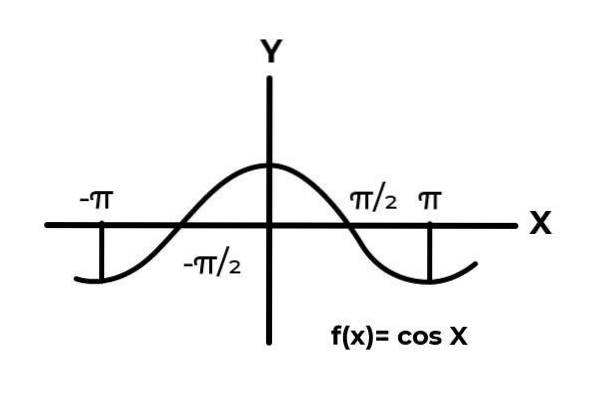
Som det kan ses i grafen. Start fra bunden ind x = -π / 2 når derefter et maksimum på nul. Det er efter x = 0 at værdierne begynder at gentage, indtil de vender tilbage til nul i x = π / 2. På denne måde er det kendt, at F (x) = Cos (x) er ikke injektionsdygtig for intervallet [ -π / 2, π / 2 ] .
Når du studerer grafen for funktionen F (x) = Cos (x) intervaller observeres, hvor kurvens opførsel tilpasser sig injektionskriterierne. Som for eksempel intervallet
[0 , π ]
Hvor funktionen varierer resulterer fra 1 til -1 uden at gentage nogen værdi i den afhængige variabel.
På denne måde fungerer funktionen F: [0 , π ] → R defineret af F (x) = Cos (x). Det er injektionsdygtigt
Der er ikke-lineære funktioner, hvor lignende tilfælde forekommer. For udtryk af rationel type, hvor nævneren indeholder mindst en variabel, er der begrænsninger, der forhindrer injektionsevnen af forholdet.
Eksempel 4
Lad funktionen fungere F: R → R defineret af F (x) = 10 / x
Funktionen er defineret for alle reelle tal undtagen 0 der har en ubestemmelighed (kan ikke deles med nul).
Når man nærmer sig nul fra venstre, tager den afhængige variabel meget store negative værdier, og umiddelbart efter nul tager værdierne for den afhængige variabel store positive tal.
Denne forstyrrelse forårsager udtrykket F: R → R defineret af F (x) = 10 / x
Vær ikke injektionsdygtig.
Som det ses i de foregående eksempler tjener udelukkelsen af værdier i domænet til at "reparere" disse ubestemmelser. Vi fortsætter med at udelukke nul fra domænet og efterlader afgangs- og ankomstsættene defineret som følger:
R - 0 → R
Hvor R - 0 symboliserer realerne undtagen et sæt, hvis eneste element er nul.
På denne måde udtrykket F: R - 0 → R defineret af F (x) = 10 / x er injektionsdygtig.
Eksempel 5
Lad funktionen fungere F: [0 , π ] → R defineret af F (x) = Sen (x)
I intervallet [0 , π ] sinusfunktionen varierer dens resultater mellem nul og en.
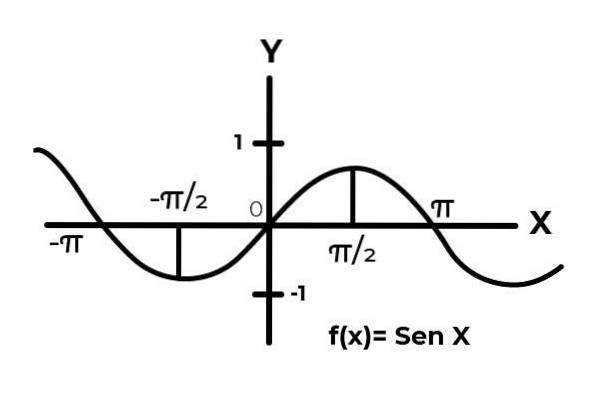
Som det kan ses i grafen. Start fra bunden ind x = 0 derefter når et maksimum i x = π / 2. Det er efter x = π / 2, som værdierne begynder at gentage, indtil de vender tilbage til nul x = π. På denne måde er det kendt, at F (x) = Sen (x) er ikke injektionsdygtig for intervallet [0 , π ] .
Når du studerer grafen for funktionen F (x) = Sen (x) intervaller observeres, hvor kurvens opførsel tilpasser sig injektionskriterierne. Som for eksempel intervallet [ π / 2,3π / 2 ]
Hvor funktionen varierer resulterer fra 1 til -1 uden at gentage nogen værdi i den afhængige variabel.
På denne måde funktionen F: [ π / 2,3π / 2 ] → R defineret af F (x) = Sen (x). Det er injektionsdygtigt
Eksempel 6
Kontroller, om funktionen F: [0, ∞) → R defineret af F (x) = 3xto det er injektionsdygtigt.
Denne gang er udtrykets domæne allerede begrænset. Det bemærkes også, at værdierne for den afhængige variabel ikke gentager sig selv i dette interval.
Derfor kan det konkluderes, at F: [0, ∞) → R defineret af F (x) = 3xto det er injektionsdygtigt
Eksempel 7
Identificer, hvilken af følgende funktioner der er
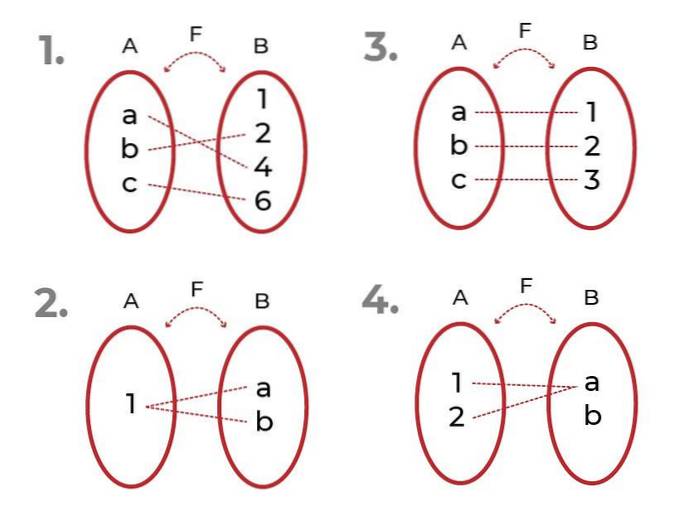
- Det er injektionsdygtigt. De tilknyttede elementer i kodomænet er unikke for hver værdi af den uafhængige variabel.
- Det er ikke injektionsdygtigt. Der er elementer i codomain forbundet med mere end et element i startsættet.
- Det er injektionsdygtigt
- Det er ikke injektionsdygtigt
Foreslåede øvelser til klasse / hjem
Kontroller, om følgende funktioner er injektionsdygtige:
F: [0, ∞) → R defineret af F (x) = (x + 3)to
F: [ π / 2,3π / 2 ] → R defineret af F (x) = Tan (x)
F: [ -π,π ] → R defineret af F (x) = Cos (x + 1)
F: R → R defineret af linjen F (x) = 7x + 2
Referencer
- Introduktion til logik og kritisk tænkning. Merrilee H. Laks. University of Pittsburgh
- Problemer i matematisk analyse. Piotr Biler, Alfred Witkowski. University of Wroclaw. Polen.
- Elementer af abstrakt analyse. Mícheál O'Searcoid PhD. Institut for matematik. University College Dublin, Beldfield, Dublind 4.
- Introduktion til logik og metodikken for de deduktive videnskaber. Alfred Tarski, Oxford i New York. Oxford University presse.
- Principper for matematisk analyse. Enrique Linés Escardó. Redaktionel Reverté S. A 1991. Barcelona Spanien.


Endnu ingen kommentarer