Det logaritmisk funktion er et matematisk forhold, der forbinder hvert positive reelle tal x med sin logaritme Y på en base til. Denne relation opfylder kravene for at være en funktion: hvert element x, der tilhører domænet, har et unikt billede.
Derfor:
f (x) = y = logtil x , med en> 0 og forskellig fra 1.
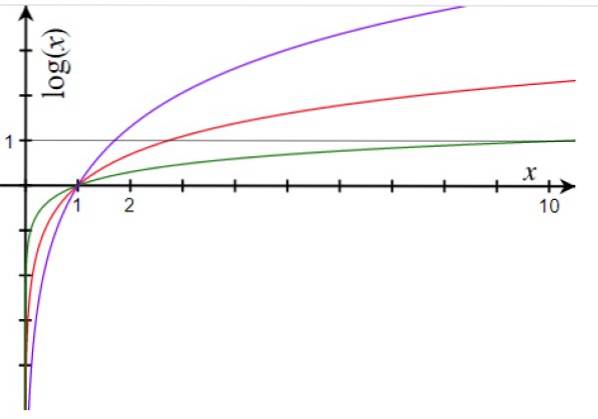
De vigtigste egenskaber ved den logaritmiske funktion er:
-Dets domæne er alle reelle større end 0, inklusive 0. Med andre ord er der ingen logaritme på 0 eller negative tal i nogen base. I intervalform:
Sol F = (0, ∞ +)
-Logaritmen for et tal kan være negativ, positiv eller 0, så dets rækkevidde eller interval er:
Rgo F = (-∞, ∞ +)
-Den logaritmiske funktion øges altid for a> 1 og falder for a<1.
-Den omvendte af f (x) = logtil x er den eksponentielle funktion.
Faktisk er logaritmefunktionen baseret på den inverse funktion af den potentielle funktion:
F-1(x) = aY
Siden logaritmen i basen til af et nummer x, Det er antallet Y som basen skal hæves til til at få x.
-Basens logaritme er altid 1. Grafen for f (x) = logtil x skærer altid x-aksen ved punktet (1,0)
-Den logaritmiske funktion er transcendent og det kan ikke udtrykkes som et polynom eller som en kvotient af disse. Ud over logaritmen inkluderer denne gruppe blandt andet de trigonometriske og eksponentielle funktioner.
Artikelindeks
Den logaritmiske funktion kan etableres ved forskellige baser, men de mest anvendte er 10 og og, hvor og er Euler-tallet lig med 2.71828 ... .
Når basen 10 bruges, kaldes logaritmen en decimal logaritme, vulgær logaritme, Briggs eller bare logaritme.
Og hvis tallet e bruges, kaldes det en naturlig logaritme af John Napier, den skotske matematiker, der opdagede logaritmer..
Notationen anvendt til hver enkelt er følgende:
-Decimal logaritme: log10 x = log x
-Naturlig logaritme: ln x
Når en anden base skal bruges, er det absolut nødvendigt at angive det som et abonnement, fordi logaritmen for hvert nummer er forskellig afhængigt af basen, der skal bruges. For eksempel, hvis det er logaritmer i base 2, skriv:
y = logto x
Lad os se på logaritmen for nummeret 10 i tre forskellige baser for at illustrere dette punkt:
log 10 = 1
ln 10 = 2.30259
logto 10 = 3.32193
Almindelige regnemaskiner bringer kun decimallogaritmer (logfunktion) og naturlig logaritme (ln-funktion). På Internettet er der lommeregnere med andre baser. Under alle omstændigheder kan læseren med sin hjælp kontrollere, at ovenstående værdier er sande:
101 = 10
og2.3026 = 10.0001
to3.32193 = 10,0000
Små decimalforskelle skyldes antallet af decimaler taget ved beregning af logaritmen.
Blandt fordelene ved at bruge logaritmer er den lethed, de giver at arbejde med store tal, ved hjælp af deres logaritme i stedet for antallet direkte.
Dette er muligt, fordi logaritmefunktionen vokser langsommere, når tallene bliver større, som vi kan se i grafen.
Så selv med meget store tal er deres logaritmer meget mindre, og det er altid lettere at manipulere med små tal..
Desuden har logaritmer følgende egenskaber:
-Produkt: log (a.b) = log a + log b
-Kvotient: log (a / b) = log a - log b
-Strøm: log enb = b.log a
Og på denne måde bliver produkterne og kvotienterne tilføjelser og subtraktioner af mindre antal, mens forstærkning bliver et simpelt produkt, selvom kraften er høj..
Derfor tillader logaritmer os at udtrykke tal, der varierer i meget store værdiområder, såsom lydens intensitet, en opløsnings pH, stjernernes lysstyrke, den elektriske modstand og intensiteten af jordskælv på Richter-skalaen..
Lad os se et eksempel på håndtering af logaritmernes egenskaber:
Find værdien af x i følgende udtryk:
log (5x +1) = 1 + log (2x-1)
Vi har her en logaritmisk ligning, da det ukendte er i logaritmens argument. Det løses ved at efterlade en enkelt logaritme på hver side af ligestillingen.
Vi starter med at placere alle de termer, der indeholder "x" til venstre for ligestillingen, og dem, der kun indeholder tal til højre:
log (5x + 1) - log (2x-1) = 1
Til venstre har vi subtraktion af to logaritmer, som kan skrives som logaritmen for et kvotient:
log [(5x + 1) / (2x-1)] = 1
Men til højre er tallet 1, som vi kan udtrykke som log 10, som vi så tidligere. Derefter:
log [(5x + 1) / (2x-1)] = log 10
For at lighed skal opfyldes, argumenter af logaritmerne skal være ens:
(5x + 1) / (2x-1) = 10
5x + 1 = 10 (2x - 1)
5x + 1 = 20 x - 10
-15 x = -11
x = 11/15
I 1957 opstod der et jordskælv i Mexico, hvis styrke var 7,7 på Richter-skalaen. I 1960 opstod der et andet jordskælv af større styrke i Chile på 9,5.
Beregn, hvor mange gange jordskælvet i Chile var mere intenst end det i Mexico, idet du vidste, at størrelsen MR på Richter-skalaen er det givet med formlen:
MR = log (104 JEG)
Størrelsen på Richters skala af et jordskælv er en logaritmisk funktion. Vi skal beregne intensiteten af hvert jordskælv, da vi har Richter-størrelserne. Lad os gøre det trin for trin:
-Mexico: 7,7 = log (104 JEG)
Da den inverse af logaritmefunktionen er den eksponentielle, anvender vi dette på begge sider af ligestillingen med den hensigt at løse for I, som findes i logaritmens argument.
Da de er decimallogaritmer, er basen 10. Derefter:
10 7.7 = 104 jeg
Intensiteten af jordskælvet i Mexico var:
jegM = 10 7.7 / 104 = 103.7
-chili: 9.5 = log (104 JEG)
Den samme procedure fører os til intensiteten af det chilenske jordskælv ICh:
jegCh = 10 9.5 / 104 = 105.5
Nu kan vi sammenligne begge intensiteter:
jegCh / JegM = 105.5 / 103.7 = 101.8 = 63,1
jegCh = 63,1. jegM
Jordskælvet i Chile var omkring 63 gange mere intenst end det i Mexico. Da størrelsen er logaritmisk, vokser den langsommere end intensiteten, så en forskel på 1 i størrelsen betyder en 10 gange større amplitude af den seismiske bølge.
Forskellen mellem størrelsen af begge jordskælv er 1,8, derfor kunne vi forvente en forskel i intensiteter tættere på 100 end til 10, som det faktisk skete..
Faktisk, hvis forskellen havde været nøjagtigt 2, ville det chilenske jordskælv have været 100 gange mere intens end det mexicanske..
Endnu ingen kommentarer