
Grad af et polynom, hvordan det bestemmes, eksempler og øvelser
Det grad af et polynom på -en variabel er givet ved det udtryk, der har den største eksponent, og hvis polynomet har to eller flere variabler, derefter bestemmes graden af summen af eksponenterne for hvert udtryk, den større sum er graden af polynomet.
Lad os se, hvordan man bestemmer graden af polynomet på en praktisk måde.

Antag, at polynomet P (x) = -5x + 8x3 + 7 - 4xto. Dette polynom er en variabel, i dette tilfælde er det variablen x. Dette polynom består af flere udtryk, som er følgende:
-5x; 8x3; 7; - 4xto
Lad os vælge blandt de fire termer, hvis eksponent er større, dette udtryk er:
8x3
Og hvad er nu eksponenten? Svaret er 3. Derfor er P (x) et polynom af grad 3.
Hvis det pågældende polynom har mere end en variabel, kan graden være:
-Absolut
-I forhold til en variabel
Den absolutte grad findes som forklaret i starten: tilføjelse af eksponenterne for hver periode og valg af den største.
På den anden side er graden af polynomet med hensyn til en af variablerne eller bogstaverne den største værdi af eksponenten, som nævnte brev har. Pointen bliver tydeligere med eksemplerne og de løste øvelser i de følgende afsnit.
Artikelindeks
- 1 Eksempler på grad af et polynom
- 1.1 Tabel 1. Eksempler på polynomer og deres grader
- 2 Fremgangsmåde til arbejde med polynomer
- 2.1 Bestil, reducer og udfyld et polynom
- 2.2 Betydningen af graden af et polynom i tillæg og subtraktion
- 3 Løst øvelser
- 3.1 - Øvelse løst 1
- 3.2 - Øvelse løst 2
- 4 Referencer
Eksempler på grad af et polynom
Polynomer kan klassificeres efter grad og kan være første grad, anden grad, tredje grad og så videre. For eksemplet i figur 1 er energien et monomium af den første grad for massen.
Det er også vigtigt at bemærke, at antallet af udtryk, som et polynom har, er lig med lønklasse plus 1. A) Ja:
-Første grads polynomer har to udtryk: a1x + aeller
-Andegradens polynom har 3 udtryk: atoxto + til1x + aeller
-Et polynomium i tredje grad har 4 udtryk: a3x3 + tiltoxto + til1x + aeller
Og så videre. Den omhyggelige læser vil have bemærket, at polynomierne i de foregående eksempler er skrevet i form faldende, dvs. placere udtrykket først med Højeste karakter.
Den følgende tabel viser forskellige polynomer, både af en og flere variabler og deres respektive absolutte grader:
Tabel 1. Eksempler på polynomer og deres grader
| Polynom | karakter |
|---|---|
| 3x4+5x3-2x + 3 | 4 |
| 7x3-2xto+3x-6 | 3 |
| 6 | 0 |
| x-1 | 1 |
| x5-bx4+abx3+ab3xto | 6 |
| 3x3Y5 + 5xtoY4 - 7xyto + 6 | 8 |
De sidste to polynomer har mere end en variabel. Af disse er udtrykket med den højeste absolutte grad fremhævet med fed skrift, så læseren hurtigt kan kontrollere graden. Det er vigtigt at huske, at når variablen ikke har en skriftlig eksponent, forstås det, at eksponenten er lig med 1.
For eksempel i det fremhævede udtryk ab3xto der er tre variabler, nemlig: til, b Y x. I det begreb, til hæves til 1, det vil sige:
a = a1
Derfor ab3xto = a1b3xto
Da eksponenten for b er 3 og den for x er 2, følger det straks, at graden af dette udtryk er:
1 + 3 + 2 = 6
Y er den absolutte grad af polynomet, da intet andet udtryk har en højere grad.
Fremgangsmåde til arbejde med polynomer
Når du arbejder med polynomer, er det vigtigt at være opmærksom på graden af det, da det først og før du udfører en operation, er det bekvemt at følge disse trin, hvor graden giver meget vigtig information:
-Bestil polynomiet af præference i faldende retning. På denne måde er udtrykket med den højeste grad til venstre og udtrykket med den laveste grad til højre..
-Reducer lignende udtryk, en procedure, der består i at tilføje algebraisk alle termerne for den samme variabel og grad, der findes i udtrykket.
-Hvis det er nødvendigt, udfyldes polynomierne og indsætter termer, hvis koefficient er 0, hvis der mangler udtryk med en eller anden eksponent.
Bestil, reducer og udfør et polynom
Givet polynomet P (x) = 6xto - 5x4- 2x + 3x + 7 + 2x5 - 3x3 + x7 -12 bliver det bedt om at bestille det i faldende rækkefølge, reducere de lignende vilkår, hvis der er nogen, og udfyld de manglende vilkår, hvis det er nødvendigt.
Den første ting at kigge efter er udtrykket med den største eksponent, som er graden af polynomet, som viser sig at være:
x7
Derfor er P (x) af grad 7. Derefter ordnes polynomet, startende med dette udtryk til venstre:
P (x) = x7 + 2x5 - 5x4 - 3x3 + 6xto - 2x + 3x + 7-12
Nu er de samme vilkår reduceret, som er følgende: - 2x og 3x på den ene side. Og 7 og -12 på den anden. For at reducere dem tilføjes koefficienterne algebraisk, og variablen efterlades uændret (hvis variablen ikke vises ved siden af koefficienten, skal du huske at x0 = 1):
-2x + 3x = x
7 -12 = -5
Erstat disse resultater i P (x):
P (x) = x7 +2x5 - 5x4 - 3x3 + 6xto + x -5
Og endelig undersøges polynomet for at se, om nogen eksponent mangler, og faktisk mangler et udtryk, hvis eksponent er 6, derfor er det afsluttet med nuller som dette:
P (x) = x7 + 0x6 +2x5 - 5x4 - 3x3 + 6xto + x - 5
Nu observeres det, at polynomet blev efterladt med 8 termer, da antallet af udtryk som sagt er lig med grad + 1.
Betydningen af graden af et polynom i tillæg og subtraktion
Med polynomier kan du udføre additions- og subtraktionsoperationer, hvor kun lignende udtryk tilføjes eller trækkes fra, hvilket er dem med samme variabel og samme grad. Hvis der ikke er nogen lignende udtryk, angives tilføjelsen eller subtraktionen simpelthen.
Når først additionen eller subtraktionen er udført, hvor sidstnævnte er summen af det modsatte, er graden af det resulterende polynom altid lig med eller mindre end graden af polynomet, der tilføjer den højeste grad.
Løst øvelser
- Løst øvelse 1
Find følgende sum, og bestem dens absolutte grad:
til3- 8axto + x3 + 5. pladstox - 6axto - x3 + 3.3 - 5. pladstox - x3 + til3+ 14axto - x3
Opløsning
Det er et polynom med to variabler, så det er praktisk at reducere lignende udtryk:
til3- 8axto + x3 + 5. pladstox - 6axto - x3 + 3.3 - 5. pladstox - x3 + til3+ 14axto - x3 =
= a3 + 3.3 + til3 - 8axto - 6axto+ 14axto +5. pladstox - 5.tox + x3- x3- x3- x3 =
= 5a3 - 2x3
Begge udtryk er af grad 3 i hver variabel. Derfor er den absolutte grad af polynomet 3.
- Træning løst 2
Udtryk området for den følgende plane geometriske figur som et polynom (figur 2 til venstre). Hvad er graden af det resulterende polynom?
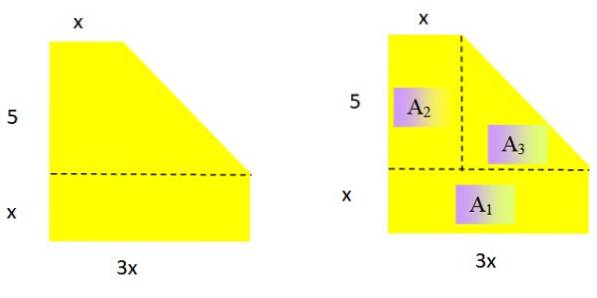
Opløsning
At være et område skal det resulterende polynom være af grad 2 i variablen x. For at bestemme et passende udtryk for området nedbrydes figuren i kendte områder:
Arealet af et rektangel og en trekant er henholdsvis: base x højde Y bund x højde / 2
TIL1 = x. 3x = 3xto; TILto = 5. x = 5x; TIL3 = 5. (2x / 2) = 5x
Bemærk: bunden af trekanten er 3x - x = 2x og dens højde er 5.
Nu tilføjes de tre opnåede udtryk, med dette har vi arealet af figuren som en funktion af x:
3xto + 5x + 5x = 3xto + 10x
Referencer
- Baldor, A. 1974. Elementær algebra. Cultural Venezolana S.A.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Wikibooks. Polynomer. Gendannet fra: es. wikibooks.org.
- Wikipedia. Grad (polynom). Gendannet fra: es.wikipedia.org.
- Zill, D. 1984. Algebra og trigonometri. Mac Graw Hill.


Endnu ingen kommentarer