EN hypercube er en terning af dimension n. Det særlige tilfælde af den firedimensionelle hypercube kaldes tesseract. En hyperkube eller n-terning består af lige segmenter, alle med lige længde, der er vinkelrette i deres hjørner.
Mennesker opfatter et tredimensionelt rum: bredde, højde og dybde, men det er ikke muligt for os at visualisere en hyperterning med en dimension større end 3.
I det højeste kan vi fremstille fremspring af det i et tredimensionelt rum for at repræsentere det på en lignende måde som hvordan vi projicerer en terning på et plan for at repræsentere den..
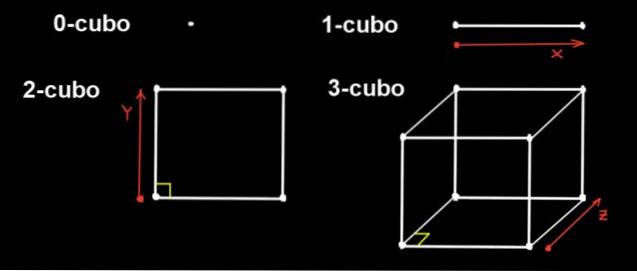
I dimension 0 er den eneste figur punktet, så en 0-terning er et punkt. En 1-terning er et lige segment, der dannes ved at flytte et punkt i en retning en afstand a.
For sin del er en 2-terning en firkant. Den er konstrueret ved at forskyde 1-terningen (længdesegmentet a) i y-retningen, som er vinkelret på x-retningen, en afstand a.
3-terningen er den almindelige terning. Den er bygget fra pladsen ved at flytte den i den tredje retning (z), som er retvinklet i retning af x og y, en afstand til.
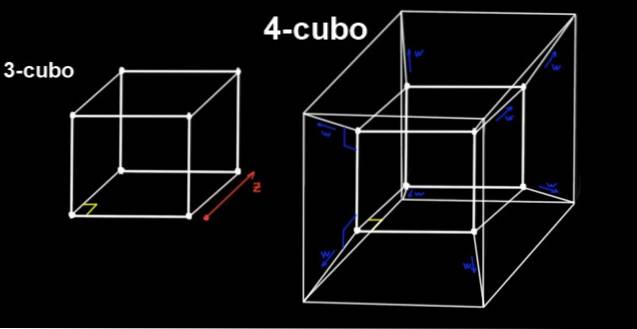
4-terningen er tesserakt, som er bygget fra en 3-terning, der forskyder den vinkelret, en afstand til, mod en fjerde dimension (eller fjerde retning), som vi ikke kan opfatte.
En tesseract har alle sine rette vinkler, den har 16 hjørner, og alle dens kanter (18 i alt) har samme længde til.
Hvis længden af kanterne på en n-terning eller hyperterning af dimension n er 1, så er det en enhedshyperterning, hvor den længste diagonale måling √n.
Artikelindeks
Dimensioner er frihedsgraderne eller de mulige retninger, som et objekt kan bevæge sig i.
I dimension 0 er der ingen mulighed for at oversætte, og det eneste mulige geometriske objekt er pointen.
En dimension i det euklidiske rum er repræsenteret af en orienteret linje eller akse, der definerer den dimension, kaldet X-aksen. Adskillelsen mellem to punkter A og B er den euklidiske afstand:
d = √ [(xtil - xb)to].
I to dimensioner er rummet repræsenteret af to linjer, der er vinkelrette på hinanden, kaldet X-aksen og Y-aksen..
Placeringen af ethvert punkt i dette todimensionelle rum er givet ved dets par kartesiske koordinater (x, y), og afstanden mellem to punkter A og B vil være:
d = √ [(xtil - xb)to + (Ytil - Yb)to]
Fordi det er et rum, hvor Euclids geometri er opfyldt.
Tredimensionelt rum er det rum, hvor vi bevæger os. Den har tre retninger: bredde, højde og dybde.
I et tomt rum giver hjørnerne vinkelret på hinanden disse tre retninger, og til hver enkelt kan vi knytte en akse: X, Y, Z.
Dette rum er også euklidisk, og afstanden mellem to punkter A og B beregnes som følger:
d = √ [(xtil - xb)to + (Ytil - Yb)to + (ztil - zb)to]
Mennesker kan ikke opfatte mere end tre rumlige (eller euklidiske) dimensioner.
Fra et strengt matematisk synspunkt er det imidlertid muligt at definere et n-dimensionelt euklidisk rum.
I dette rum har et punkt koordinater: (x1, x2, x3,…, xn) og afstanden mellem to punkter er:
d = √ [(x1. - x1 B)to + (x2. plads - x2b)to +… + (Xna - xnb)to].
Faktisk behandles tiden i relativitetsteorien som en yderligere dimension, og en koordinat er forbundet med den.
Men det skal præciseres, at denne koordinat forbundet med tiden er et imaginært tal. Adskillelsen af to punkter eller begivenheder i rumtid er derfor ikke euklidisk, men følger snarere Lorentz-metricen.
En firedimensionel hyperkube (tesseract) lever ikke i rumtid, den hører til et firedimensionelt euklidisk hyperrum.
Koordinaterne for hjørnerne af en n-terning centreret ved oprindelsen opnås ved at udføre alle mulige permutationer af følgende udtryk:
(a / 2) (± 1, ± 1, ± 1,…., ± 1)
Hvor a er kantlængden.
-Det bind af en n-terning af kant a er: (a / 2)n (ton) = an.
-Det længste diagonal er afstanden mellem modsatte hjørner.
-Følgende er modsatte hjørner i en firkant: (-1, -1) og (+1, +1).
-Og i en Terning: (-1, -1, -1) og (+1, +1, +1).
-Det længste diagonal af en n-terning måler:
d = √ [1 - (- 1))to +… + (1 - (- 1))to] = √ [n 2to] = 2√n
I dette tilfælde blev siden antaget at være a = 2. For en n-terning på en hvilken som helst side forbliver følgende:
d = a√n.
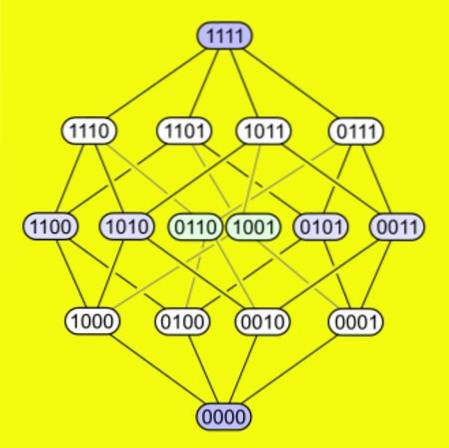
-En tesseract har hver af sine 16 hjørner forbundet med fire kanter. Følgende figur viser, hvordan hjørner er forbundet i en tesserakt.
En regelmæssig geometrisk figur, for eksempel en polyhedron, kan foldes ud i flere figurer af mindre dimensionalitet.
I tilfælde af en 2-terning (en firkant) kan den foldes ud i fire segmenter, det vil sige fire 1-terninger.
Tilsvarende kan en 3-terning foldes ud i seks 2-terninger.
En 4-terning (tesseract) kan foldes ud i otte 3-terninger.
Følgende animation viser udfoldelsen af en tesserakt.
Endnu ingen kommentarer