Coulombs lovforklaring, formel og enheder, øvelser, eksperimenter

Det Coulomb lov det er den fysiske lov, der styrer interaktionen mellem elektrisk ladede genstande. Det blev udråbt af den franske videnskabsmand Charles Augustin de Coulomb (1736-1806) takket være resultaterne af hans eksperimenter ved hjælp af torsionsbalancen.

I 1785 eksperimenterede Coulomb utallige gange med små elektrisk ladede kugler, for eksempel at flytte to kugler tættere eller længere fra hinanden, varierende størrelsen af ​​deres ladning og også deres tegn. Overhold og registrer altid hvert svar omhyggeligt.

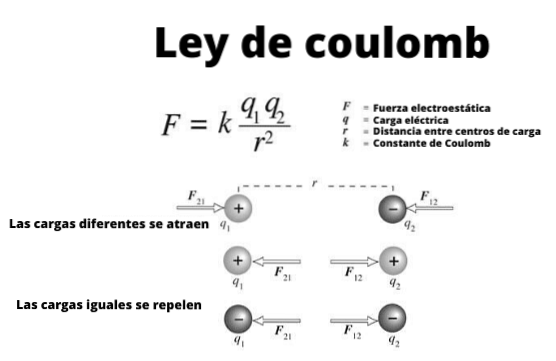
Disse små kugler kan betragtes som punktbelastninger, objekter, hvis dimensioner er ubetydelige. Og de opfylder, som det har været kendt siden de antikke grækeres tid, at anklager for det samme tegn frastøder og de af et andet tegn tiltrækker..

Med dette i tankerne fandt Charles Coulomb følgende:

-Den tiltrækkende eller frastødende kraft mellem topunktsladninger er direkte proportional med produktet af ladningernes størrelse.

-Denne kraft er altid rettet langs den linje, der slutter sig til anklagerne.

-Endelig er kraftens størrelse omvendt proportional med kvadratet for afstanden mellem ladningerne.

Artikelindeks

• 1 Formel og enheder af Coulombs lov
• 2 Sådan anvendes Coulombs lov
• 3 Løst øvelser
  • 3.1 - Øvelse 1
  • 3.2 - Øvelse 2
• 4 eksperimenter
• 5 Referencer

Formel og enheder af Coulombs lov

Takket være disse observationer konkluderede Coulomb, at styrkeens størrelse F mellem to punktafgifter hvad₁ Y hvad_to, adskilt en afstand r, er matematisk givet som:

Da kraften er en vektorstørrelse, defineres en enhedsvektor for at udtrykke den fuldstændigt r i retning af linjen, der forbinder ladningerne (en enhedsvektor har en størrelse lig med 1).

Derudover kaldes den konstante proportionalitet, der er nødvendig for at omdanne det tidligere udtryk til en lighed, k_og eller simpelthen k: elektrostatisk konstant eller Coulomb er konstant.

Endelig er Coulombs lov oprettet for punktafgifter givet af:

Kraft, som altid i det internationale enhedssystem, kommer i newton (N). Med hensyn til afgifterne hedder enheden coulomb (C) til ære for Charles Coulomb, og endelig kommer afstanden r i meter (m).

Når man ser nøje på ovenstående ligning, er det klart, at den elektrostatiske konstant skal have enheder på N.m^to / C^to, for at få newton som et resultat. Værdien af ​​konstanten blev bestemt eksperimentelt som:

k_og = 8,89 x 10 ⁹ N.m^to / C^to ≈ 9 x 10 ⁹ N.m^to / C^to

Figur 1 illustrerer samspillet mellem to elektriske ladninger: når de har samme tegn, frastøder de, ellers tiltrækker de.

Bemærk, at Coulombs lov er i overensstemmelse med Newtons tredje lov eller handlings- og reaktionslov, derfor størrelsen af F₁ Y F_to de er de samme, retningen er den samme, men sanserne er modsatte.

Sådan anvendes Coulombs lov

For at løse problemer med interaktioner mellem elektriske ladninger skal følgende tages i betragtning:

- Ligningen gælder udelukkende i tilfælde af punktladninger, det vil sige elektrisk ladede genstande, men med meget små dimensioner. Hvis de indlæste objekter har målbare dimensioner, er det nødvendigt at opdele dem i meget små belastninger og derefter tilføje bidragene fra hver af disse belastninger, for hvilke der kræves en integreret beregning..

- Den elektriske kraft er en vektormængde. Hvis der er mere end to interaktive ladninger, er nettokraften på ladningen q_jeg er givet ved superpositionsprincippet:

F_net = F_i1 + F_i2 + F_i3 + F_i4 +… = ∑ F_ij

Hvor abonnementet j er lig med 1, 2, 3, 4 ... og repræsenterer hver af de resterende afgifter.

- Du skal altid være i overensstemmelse med enhederne. Den hyppigste ting er at arbejde med den elektrostatiske konstant i SI-enheder, så er det nødvendigt at sikre, at ladningerne er i coulomb og afstanden i meter.

- Endelig gælder ligningen, når ladningerne er i statisk ligevægt.

Løst øvelser

- Øvelse 1

I den følgende figur er der to punktafgifter + q og + 2q. En tredje punkt-ladning -q placeres ved P. Det bliver bedt om at finde den elektriske kraft på denne ladning på grund af tilstedeværelsen af ​​de andre.

Opløsning

Den første ting er at etablere et passende referencesystem, som i dette tilfælde er den vandrette akse eller x-aksen. Oprindelsen til et sådant system kan være hvor som helst, men for nemheds skyld placeres det på P som vist i figur 4a:

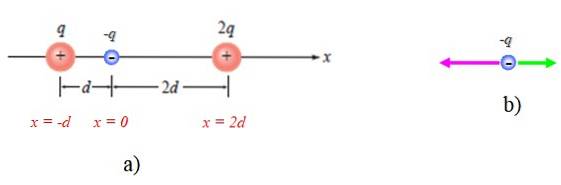
Et diagram over kræfterne på -q vises også under hensyntagen til, at det er tiltrukket af de to andre (figur 4b).

Lad os ringe F₁ den kraft, der udøves af ladning q på ladning -q, er rettet langs x-aksen og peger i negativ retning, derfor:

Analogt beregnes det F_to:

Bemærk, at størrelsen på F_to er halvdelen af ​​den af F₁, selvom belastningen er dobbelt. For at finde nettokraften tilføjes de endelig vektorielt F₁ Y F_to:

F_net = (-k + k / 2). (q^to / d^to) (x) N = - (k / 2). (Q^to / d^to) (x) N

- Øvelse 2

To polystyrenkugler med samme masse m = 9,0 x 10^-8 kg har den samme positive ladning Q og er ophængt af en silketråd med længden L = 0,98 m. Kuglerne er adskilt med en afstand på d = 2 cm. Beregn værdien af ​​Q.

Opløsning

Udtalelsessituationen er beskrevet i figur 5a.

Vi vælger en af ​​kuglerne og på den tegner vi det isolerede kropsdiagram, som inkluderer tre kræfter: vægt W, spænding i rebet T og elektrostatisk frastødning F, som det fremgår af figur 5b. Og nu trinene:

Trin 1

Værdien af ​​θ / 2 beregnes med trekanten i figur 5c:

θ / 2 = lysbue (1 x 10^-to/0,98) = 0,585º

Trin 2

Dernæst skal vi anvende Newtons anden lov og sætte den lig med 0, da ladningerne er i statisk ligevægt. Vigtigere er spændingen T er skråt og har to komponenter:

∑F_x = -T.sin θ + F = 0

∑F_Y = T.cos θ - W = 0

Trin 3

Vi løser størrelsen af ​​spændingen fra den sidste ligning:

T = W / cos θ = mg / cos θ

Trin 4

Denne værdi erstattes af den første ligning for at finde størrelsen af ​​F:

F = T sin θ = mg (sin θ / cos θ) = mg. tg θ

Trin 5

Da F = k Q^to / d^to, rydder Q:

Q = 2 × 10^-elleve C.

Eksperimenter

Det er let at kontrollere Coulombs lov ved hjælp af en torsionsbalance svarende til den, Coulomb brugte i hans laboratorium..

Der er to små hyldebærsfærer, hvoraf den ene i midten af ​​vægten er ophængt af en tråd. Eksperimentet består i at røre de udledte hyldebærkugler med en anden metallisk kugle, der er ladet med Q-ladning.

Straks fordeles ladningen ligeligt mellem de to hyldebærsfærer, men da de er ladninger af det samme tegn frastøder de hinanden. En kraft virker på den ophængte kugle, der forårsager vridning af tråden, hvorfra den hænger, og straks bevæger sig væk fra den faste kugle.

Så ser vi, at det svinger et par gange, indtil det når ligevægt. Derefter afbalanceres torsionen på stangen eller tråden, der holder den, af den elektrostatiske frastødningskraft.

Hvis kuglerne oprindeligt var på 0 °, vil den bevægelige kugle nu have drejet en vinkel θ. Omkring skalaen er der et bånd gradueret i grader for at måle denne vinkel. Ved tidligere at bestemme torsionskonstanten beregnes den frastødende kraft og værdien af ​​ladningen erhvervet af hyldebærsfærerne let.

Referencer

1. Figueroa, D. 2005. Serie: Physics for Sciences and Engineering. Volumen 5. Elektrostatik. Redigeret af Douglas Figueroa (USB).
2. Giambattista, A. 2010. Fysik. Anden version. Mcgraw bakke.
3. Giancoli, D. 2006. Fysik: Principper med applikationer. 6. Ed prentice hall.
4. Resnick, R. 1999. Fysik. Bind 2. 3. udgave på spansk. Compañía Editorial Continental S.A. af C.V.
5. Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14. Red. Bind 2.