Det lov af Hardy-Weinberg, Også kaldet Hardy-Weinberg-princippet eller ligevægten, det består af en matematisk sætning, der beskriver en hypotetisk diploid population med seksuel reproduktion, der ikke udvikler sig - allelfrekvenser ændres ikke fra generation til generation.
Dette princip forudsætter fem nødvendige betingelser for, at befolkningen forbliver konstant: fravær af genstrøm, fravær af mutationer, tilfældig parring, fravær af naturlig selektion og en uendelig stor populationsstørrelse. På denne måde forbliver befolkningen i ligevægt i fravær af disse kræfter.
Når nogen af ovenstående antagelser ikke er opfyldt, sker der ændringer. Af denne grund er naturlig selektion, mutation, migrationer og genetisk drift de fire evolutionære mekanismer..
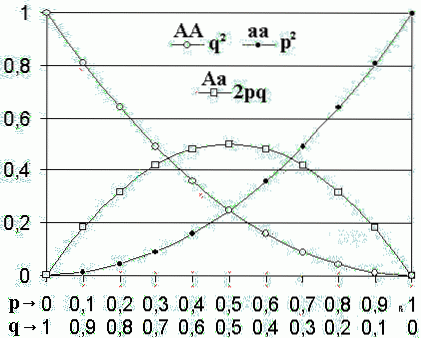
Ifølge denne model, når allelfrekvenserne for en population er s Y hvad, genotypefrekvenser vil være sto, topq Y hvadto.
Vi kan anvende Hardy-Weinberg-ligevægten til beregning af frekvenser af bestemte alleler af interesse, for eksempel for at estimere andelen af heterozygoter i en menneskelig befolkning. Vi kan også kontrollere, om en befolkning er i ligevægt eller ikke, og foreslå hypoteser om, at kræfter virker på denne befolkning..
Artikelindeks
Hardy-Weinberg-princippet blev født i 1908 og skylder sit navn forskerne G.H. Hardy og W. Weinberg, der uafhængigt nåede de samme konklusioner.
Før det havde en anden biolog ved navn Udny Yule tacklet problemet i 1902. Yule startede med et sæt gener, hvor hyppigheden af begge alleler var 0,5 og 0,5. Biologen viste, at frekvenserne blev opretholdt i de følgende generationer.
Selvom Yule konkluderede, at allelfrekvenser kunne holdes stabile, var hans fortolkning for bogstavelig. Han mente, at den eneste tilstand af ligevægt blev fundet, når frekvenserne svarede til værdien 0,5.
Yule diskuterede heftigt sine nye fund med R.C. Punnett - bredt kendt inden for genetik til opfindelsen af den berømte "Punnett-firkant". Selvom Punnett vidste, at Yule tog fejl, fandt han ikke en matematisk måde at bevise det på..
Derfor kontaktede Punnett sin matematikerven Hardy, der formåede at løse det med det samme og gentog beregningerne ved hjælp af generelle variabler og ikke den faste værdi på 0,5 som Yule havde gjort..
Befolkningsgenetik sigter mod at studere de kræfter, der fører til ændringer i allelfrekvenser i populationer, integrering af Charles Darwins teori om evolution ved naturlig selektion og mandelisk genetik. I dag giver dets principper det teoretiske grundlag for forståelse af mange aspekter af evolutionær biologi..
En af de afgørende ideer med populationsgenetik er forholdet mellem ændringer i den relative overflod af træk og ændringer i den relative overflod af de alleler, der regulerer det, forklaret af Hardy-Weinberg-princippet. Faktisk giver denne sætning den konceptuelle ramme for populationsgenetik..
På baggrund af populationsgenetik er begrebet evolution som følger: ændring i allelfrekvenser over generationer. Når der ikke er nogen ændring, er der ingen udvikling.
Hardy-Weinberg-ligevægten er en nulmodel, der giver os mulighed for at specificere opførsel af gen- og allelfrekvenser på tværs af generationer. Med andre ord er det modellen, der beskriver opførsel af gener i populationer under en række specifikke forhold..
I Hardy-Weinbergms sætning er allelfrekvensen af TIL (dominerende allel) er repræsenteret af brevet s, mens allelfrekvensen af til (recessiv allel) er repræsenteret af brevet hvad.
De forventede genotypefrekvenser er sto, topq Y hvadto, for den homozygote dominerende (AA), heterozygot (Aa) og homozygot recessiv (aa), henholdsvis.
Hvis der kun er to alleler på dette sted, skal summen af frekvenserne for de to alleler nødvendigvis være lig med 1 (p + q = 1). Binomial ekspansion (p + q)to repræsenterer genotypefrekvenser sto + topq + qto = 1.
I en befolkning krydser de individer, der komponerer det, for at give afkom. Generelt kan vi påpege de vigtigste aspekter af denne reproduktive cyklus: produktionen af kønsceller, deres fusion til at give anledning til en zygote og udviklingen af embryoet til at give anledning til den nye generation..
Forestil dig, at vi kan spore den mendeliske genproces i de nævnte begivenheder. Vi gør dette, fordi vi vil vide, om og hvorfor en allel eller genotype vil stige eller falde i frekvens..
For at forstå, hvordan gen- og allelfrekvenser varierer i en population, følger vi gametproduktionen af et sæt mus. I vores hypotetiske eksempel forekommer parring tilfældigt, hvor al sæd og æg blandes tilfældigt..
For mus er denne antagelse ikke sand og er blot en forenkling for at lette beregningerne. Men i nogle dyregrupper, såsom visse pighuder og andre vandorganismer, uddrives kønsceller og kolliderer tilfældigt..
Lad os nu fokusere vores opmærksomhed på et specifikt sted med to alleler: TIL Y til. I henhold til loven, der er foreskrevet af Gregor Mendel, modtager hver gamete en allel fra locus A. Antag at 60% af æggene og sædcellerne modtager allelen TIL, mens de resterende 40% modtog allelen til.
Derfor allelfrekvensen TIL er 0,6 og allelens til er 0,4. Denne gruppe gameter findes tilfældigt for at give anledning til en zygote. Hvad er sandsynligheden for, at de vil danne hver af de tre mulige genotyper? For at gøre dette skal vi gange sandsynlighederne som følger:
Genotype AA: 0,6 x 0,6 = 0,36.
Genotype Aa: 0,6 x 0,4 = 0,24. I tilfælde af heterozygote er der to former, hvor den kan stamme. Den første at sæd bærer allelen TIL og æggepinden allelen til, eller omvendt tilfælde, sædcellerne til og æg TIL. Derfor tilføjer vi 0,24 + 0,24 = 0,48.
Genotype aa: 0,4 x 0,4 = 0,16.
Lad os forestille os, at disse zygoter udvikler sig og bliver voksne mus, der igen vil producere kønsceller, ville vi forvente, at allelfrekvenserne er de samme eller forskellige fra den forrige generation?
Genotype AA vil producere 36% af kønsceller, mens heterozygoter vil producere 48% af kønsceller og genotypen aa 16%.
For at beregne den nye allelfrekvens tilføjer vi hyppigheden af den homozygote plus halvdelen af den heterozygote som følger:
Allelfrekvens TIL: 0,36 + ½ (0,48) = 0,6.
Allelfrekvens til: 0,16 + ½ (0,48) = 0,4.
Hvis vi sammenligner dem med de indledende frekvenser, vil vi indse, at de er identiske. Derfor er befolkningen i overensstemmelse med begrebet evolution, da der ikke er nogen ændringer i allelfrekvenser over generationer, i ligevægt - den udvikler sig ikke..
Hvilke betingelser skal den tidligere befolkning opfylde, så dens allelfrekvenser forbliver konstante gennem generationer? I Hardy-Weinberg-ligevægtsmodellen opfylder befolkningen, der ikke udvikler sig, følgende antagelser:
Befolkningen skal være ekstremt stor i størrelse for at undgå stokastiske eller tilfældige effekter af gendrift.
Når populationer er små, er effekten af gendrift (tilfældige ændringer i allelfrekvenser fra en generation til en anden) på grund af prøveudtagningsfejl meget større og kan føre til fiksering eller tab af visse alleler..
Migrationer findes ikke i befolkningen, så alleler, der kan ændre genfrekvenser, kan ikke ankomme eller forlade.
Mutationer er ændringer i DNA-sekvensen, og de kan have forskellige årsager. Disse tilfældige ændringer ændrer genpuljen i populationen ved introduktion eller eliminering af gener i kromosomerne.
Blandingen af kønscellerne skal ske tilfældigt - ligesom den antagelse, vi brugte i museksemplet. Derfor bør der ikke være et valg af partner blandt individerne i befolkningen, herunder indavl (reproduktion af individer, der er beslægtede).
Når parringen ikke er tilfældig, forårsager den ikke en ændring i allelfrekvenser fra en generation til den næste, men den kan generere afvigelser fra de forventede genotypefrekvenser..
Der er ingen differentiel reproduktiv succes for personer med forskellige genotyper, der kan ændre allelfrekvenser inden for befolkningen..
Med andre ord, i den hypotetiske population har alle genotyper den samme sandsynlighed for at reproducere og overleve..
Når en befolkning ikke opfylder disse fem betingelser, er resultatet evolution. Logisk set opfylder naturlige befolkninger ikke disse antagelser. Derfor bruges Hardy-Weinberg-modellen som en nulhypotese, der giver os mulighed for at foretage omtrentlige estimater af genet og allelfrekvenser..
Ud over manglen på disse fem betingelser er der andre mulige årsager til, at befolkningen ikke er i ligevægt.
En af disse opstår, når loci er knyttet til køn eller forvrængningsfænomener i segregering eller meiotisk drev (når hver kopi af et gen eller kromosom ikke transmitteres med lige stor sandsynlighed til den næste generation).
I USA har en anslået en ud af 10.000 nyfødte en tilstand kaldet phenylketonuri..
Denne lidelse udtrykkes kun i recessive homozygoter i en metabolisk lidelse. Kendskab til disse data, hvad er hyppigheden af bærere af sygdommen i befolkningen??
For at anvende Hardy-Weinberg ligningen må vi antage, at valget af partner ikke er relateret til genet relateret til patologien, og at der ikke er nogen indavl.
Desuden antager vi, at der ikke er nogen vandrende fænomener i USA, der er ingen nye phenylketonuri-mutationer, og sandsynligheden for reproduktion og overlevelse er den samme mellem genotyper..
Hvis ovennævnte betingelser er sande, kan vi bruge Hardy-Weinberg-ligningen til at udføre beregninger, der er relevante for problemet..
Vi ved, at der er et tilfælde af sygdommen hver 10.000 fødsler, så hvadto = 0,0001, og frekvensen af den recessive allel vil være kvadratroden af denne værdi: 0.01.
Hvad p = 1 - hvad, vi skal s er 0,99. Nu har vi frekvensen af begge alleler: 0,01 og 0,99. Bærefrekvens refererer til hyppigheden af heterozygoter, der beregnes som 2pq. Således 2pq = 2 x 0,99 x 0,01 = 0,0198.
Dette svarer til ca. 2% af befolkningen. Husk, at dette kun er et omtrentligt resultat.
Hvis vi kender antallet af hver genotype i befolkningen, kan vi konkludere, om det er i Hardy-Weinberg-ligevægten. Trinene til løsning af disse typer problemer er som følger:
p = D + ½ H
q = R + ½ H
For eksempel vil vi kontrollere, om den følgende population af sommerfugle er i Hardy-Weinberg-ligevægt: der er 79 personer med homozygot dominerende genotype (AA), 138 af heterozygoten (Aa) og 61 af den homozygote recessive (aa).
Det første trin er at beregne de observerede frekvenser. Vi gør dette ved at dividere antallet af individer pr. Genotype med det samlede antal individer:
D = 79/278 = 0,28
H = 138/278 = 0,50
R = 61/278 = 0,22
For at kontrollere, om jeg har klaret mig, er det første trin, tilføjer jeg alle frekvenser, og det skal give 1.
Det andet trin er at beregne allelfrekvenserne.
s = 0,28 + ½ (0,50) = 0,53
hvad = 0,22 + ½ (0,50) = 0,47
Med disse data kan jeg beregne de forventede genotypefrekvenser (sto, tohvorfor og hvadto)
sto = 0,28
topq = 0,50
hvadto = 0,22
Jeg beregner de forventede tal og ganger de forventede frekvenser med antallet af individer. I dette tilfælde er antallet af observerede og forventede individer identisk, så jeg kan konkludere, at befolkningen er i ligevægt.
Når de opnåede tal ikke er identiske, skal jeg anvende den nævnte statistiske test (xto fra Pearson).
Endnu ingen kommentarer