
Vector Algebra Fundamentals, Magnitudes, Vectors
Det vektor algebra er en gren af matematik med ansvar for at studere systemer med lineære ligninger, vektorer, matricer, vektorrum og deres lineære transformationer. Det er relateret til områder som teknik, opløsning af differentialligninger, funktionel analyse, operationsforskning, computergrafik, blandt andre..
Et andet område, som lineær algebra har vedtaget, er fysik, da det gennem dette har været muligt at udvikle studiet af fysiske fænomener, der beskriver dem ved hjælp af vektorer. Dette har muliggjort en bedre forståelse af universet.

Artikelindeks
- 1 Grundlæggende
- 1.1 Geometrisk
- 1.2 Analytisk
- 1.3 Aksiomatisk
- 2 størrelser
- 2.1 Skala størrelse
- 2.2 Vektorstørrelse
- 3 Hvad er vektorer?
- 3.1 Modul
- 3.2 Adresse
- 3.3 Sans
- 4 Klassifikation af vektorer
- 4.1 Fast vektor
- 4.2 Gratis vektor
- 4.3 Glidende vektor
- 5 Egenskaber for vektorer
- 5.1 teamlinsevektorer
- 5.2 Ækvivalente vektorer
- 5.3 Ligestilling af vektorer
- 5.4 Modsatte vektorer
- 5.5 Enhedsvektor
- 5.6 Null vektor
- 6 Komponenter i en vektor
- 6.1 Eksempler
- 7 Operationer med vektorer
- 7.1 Addition og subtraktion af vektorer
- 7.2 Multiplikation af vektorer
- 8 Referencer
Grundlæggende
Vektoralgebra stammer fra studiet af kvaternioner (udvidelse af reelle tal) 1, i, j og k samt fra den kartesiske geometri, der fremmes af Gibbs og Heaviside, der indså, at vektorer ville tjene som et instrument til at repræsentere forskellige fysiske fænomener.
Vektoralgebra studeres gennem tre grundlæggende:
Geometrisk
Vektorer er repræsenteret af linjer, der har en orientering, og operationer som addition, subtraktion og multiplikation med reelle tal defineres ved hjælp af geometriske metoder..
Analytisk
Beskrivelsen af vektorer og deres operationer udføres med tal, kaldet komponenter. Denne type beskrivelse er resultatet af en geometrisk fremstilling, fordi der anvendes et koordinatsystem.
Axiomatisk
En beskrivelse af vektorerne foretages, uanset koordinatsystemet eller enhver form for geometrisk repræsentation.
Undersøgelsen af figurer i rummet sker gennem deres repræsentation i et referencesystem, som kan have en eller flere dimensioner. Blandt de vigtigste systemer er:
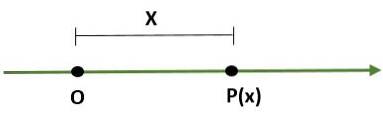
- Et-dimensionelt system, som er en linje, hvor et punkt (O) repræsenterer oprindelsen, og et andet punkt (P) bestemmer skalaen (længde) og dens retning:
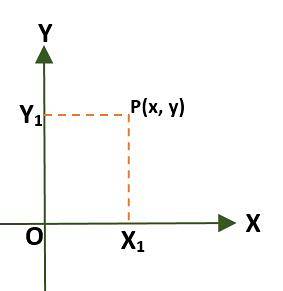
- Rektangulært koordinatsystem (to-dimensionelt), der består af to vinkelrette linjer kaldet x-aksen og y-aksen, der passerer gennem en punkt (O) oprindelse; på denne måde er flyet opdelt i fire regioner kaldet kvadranter. I dette tilfælde gives et punkt (P) i planet af afstandene, der findes mellem akserne og P.
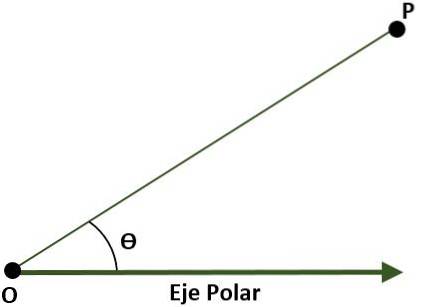
- Polært koordinatsystem (todimensionalt). I dette tilfælde er systemet sammensat af et punkt O (oprindelse), der kaldes polen og en stråle med oprindelse i O kaldet polaraksen. I dette tilfælde er punktet P på planet, med henvisning til polen og polaraksen, givet af vinklen (Ɵ), som er dannet af afstanden mellem oprindelsen og punktet P.
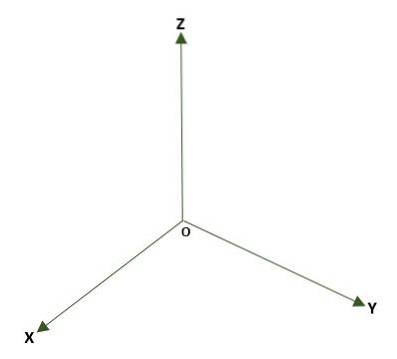
- Rektangulært tredimensionelt system dannet af tre vinkelrette linjer (x, y, z), hvis oprindelse er et punkt O i rummet. Tre koordinatplaner dannes: xy, xz og yz; rummet vil blive opdelt i otte regioner kaldet oktanter. Henvisningen til et punkt P i rummet er givet ved afstanden mellem flyene og P.
Størrelser
En størrelse er en fysisk størrelse, der kan tælles eller måles gennem en numerisk værdi, som i tilfældet med nogle fysiske fænomener; det er dog ofte nødvendigt at kunne beskrive disse fænomener med andre faktorer end numeriske. Derfor er størrelsesorden klassificeret i to typer:
Skala størrelse
De er de størrelser, der er defineret og repræsenteret numerisk; det vil sige ved et modul sammen med en måleenhed. For eksempel:
a) Tid: 5 sekunder.
b) Masse: 10 kg.
c) Volumen: 40 ml.
d) Temperatur: 40 ºC.
Vektor størrelse
De er de størrelser, der er defineret og repræsenteret af et modul sammen med en enhed såvel som en sans og retning. For eksempel:
a) Hastighed: (5ȋ - 3ĵ) m / s.
b) Acceleration: 13 m / sto; S 45º E.
c) Kraft: 280 N, 120º.
d) Vægt: -40 ĵ kg-f.
Vektormængder er repræsenteret grafisk af vektorer.
Hvad er vektorer?
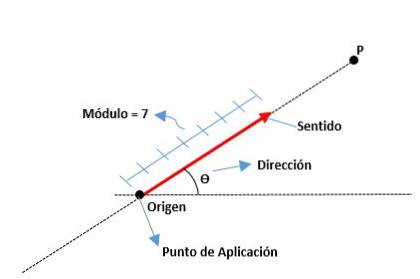
Vektorer er grafiske repræsentationer af en vektormængde; det vil sige, de er linjesegmenter, hvor deres sidste ende er spidsen af en pil.
Disse bestemmes af dets modul eller segmentlængde, dets retning, som er angivet med pilens spids, og dens retning i henhold til den linje, som den tilhører. Oprindelsen af en vektor er også kendt som anvendelsesstedet.
Elementerne i en vektor er som følger:
Modul
Det er afstanden fra oprindelsen til slutningen af en vektor, repræsenteret af et reelt tal sammen med en enhed. For eksempel:
| OM | = | A | = A = 6 cm
Retning
Det er målet for den vinkel, der findes mellem x-aksen (fra det positive) og vektoren, såvel som de kardinalpunkter (nord, syd, øst og vest) bruges.
Følelse
Det er angivet af pilespidsen, der er placeret i slutningen af vektoren, hvilket indikerer, hvor den skal hen.
Klassificering af vektorer
Generelt er vektorer klassificeret som:
Fast vektor
Det er et, hvis anvendelsessted (oprindelse) er fast; det vil sige, det forbliver knyttet til et punkt i rummet, så det kan ikke bevæge sig i dette.
Gratis vektor
Det kan bevæge sig frit i rummet, fordi dets oprindelse bevæger sig til ethvert punkt uden at ændre dets modul, retning eller retning..
Skydervektor
Det er en, der kan overføre sin oprindelse langs sin handlingslinje uden at ændre modul, retning eller retning..
Egenskaber for vektorer
Blandt de vigtigste egenskaber ved vektorer er følgende:
Vektorer holdlinser
De er de gratis vektorer, der har samme modul, retning (eller de er parallelle) og fornemmer som en glidende vektor eller en fast vektor.
Ækvivalente vektorer
Det sker, når to vektorer har samme retning (eller er parallelle), den samme sans, og på trods af at de har forskellige moduler og anvendelsespunkter, forårsager de de samme effekter.
Vector lighed
Disse har samme modul, retning og fornemmelse, selv når deres startpunkter er forskellige, hvilket gør det muligt for en parallel vektor at oversætte sig selv uden at påvirke det..
Modsatte vektorer
Det er dem, der har samme modul og retning, men deres sans er modsat.
Enhedsvektor
Det er en, hvor modulet er lig med enheden (1). Dette opnås ved at dividere vektoren med dens modul og bruges til at bestemme retningen og følelsen af en vektor, enten i planet eller i rummet ved hjælp af basis- eller normaliserede enhedsvektorer, som er:
Null vektor
Det er den, hvis modul er lig med 0; det vil sige dets oprindelses- og slutpunkt falder sammen på samme punkt.
Komponenter i en vektor
Komponenterne i en vektor er disse værdier for vektorens fremspring på akserne i referencesystemet; Afhængig af dekomponering af vektoren, som kan være på to eller tredimensionelle akser, opnås henholdsvis to eller tre komponenter..
Komponenterne i en vektor er reelle tal, som kan være positive, negative eller endda nul (0).
Således, hvis vi har en vektor Ā med oprindelse i et rektangulært koordinatsystem i xy-planet (todimensionalt), er projektionen på x-aksen Āx, og projektionen på y-aksen er Āy. Således vil vektoren blive udtrykt som summen af dens komponentvektorer.
Eksempler
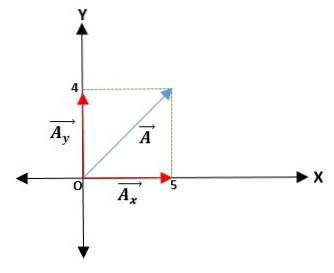
Første eksempel
Vi har en vektor Ā, der starter fra oprindelsen, og koordinaterne for dens ender er givet. Således er vektoren Ā = (Āx; TILY) = (4; 5) cm.
Hvis vektoren Ā virker ved oprindelsen af et tredimensionelt trekantet koordinatsystem (i rummet) x, y, z, til et andet punkt (P), vil fremspringene på dens akser være Āx, Āy og Āz; vektoren vil således blive udtrykt som summen af dens tre-komponentvektorer.
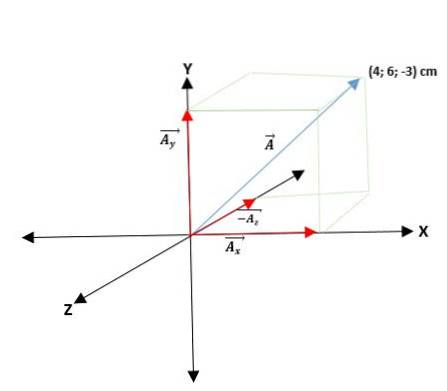
Andet eksempel
Vi har en vektor Ā, der starter fra oprindelsen, og koordinaterne for dens ender er givet. Således er vektoren Ā = (Ax; TILY; TILz) = (4; 6; -3) cm.
Vektorer, der har deres rektangulære koordinater, kan udtrykkes som deres basisvektorer. Til det er du kun nødt til at multiplicere hver koordinat med sin respektive enhedsvektor på en sådan måde, at de for flyet og rummet vil være følgende:
For flyet: Ā = Axi + A.Yj.
For rummet: Ā = A.xi + A.Yj + A.zk.
Vector operationer
Der er mange størrelser, der har et modul, sans og retning, såsom acceleration, hastighed, forskydning, kraft, blandt andre..
Disse anvendes i forskellige videnskabelige områder, og for at anvende dem er det i nogle tilfælde nødvendigt at udføre operationer såsom addition, subtraktion, multiplikation og opdeling af vektorer og skalarer..
addition og subtraktion af vektorer
Tilføjelse og subtraktion af vektorer betragtes som en enkelt algebraisk operation, fordi subtraktionen kan skrives som en sum; for eksempel kan subtraktionen af vektorerne Ā og Ē udtrykkes som:
Ā - Ē = Ā + (-Ē)
Der er forskellige metoder til at udføre addition og subtraktion af vektorer: de kan være grafiske eller analytiske.
Grafiske metoder
Anvendes når en vektor har et modul, sans og retning. Til dette trækkes linjer, der danner et tal, der senere hjælper med at bestemme resultatet. Blandt de bedst kendte er følgende:
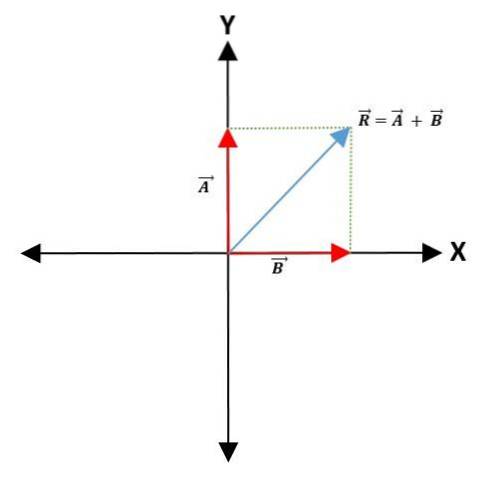
Parallelogram metode
For at foretage tilføjelse eller subtraktion af to vektorer vælges et fælles punkt på koordinataksen - som repræsenterer vektorernes oprindelsespunkt - og holder modulet, retning og retning..
Linjer tegnes derefter parallelt med vektorerne for at danne et parallelogram. Den resulterende vektor er diagonalen, der går fra begge vektorers oprindelsessted til parallelogramets toppunkt:
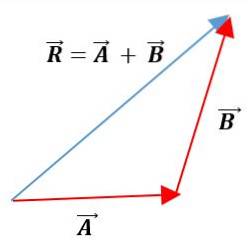
Trekantsmetode
I denne metode placeres vektorerne efter hinanden med deres moduler, retninger og retninger. Den resulterende vektor vil være foreningen af oprindelsen af den første vektor med slutningen af den anden vektor:
Analytiske metoder
To eller flere vektorer kan tilføjes eller trækkes gennem en geometrisk eller vektormetode:
Geometrisk metode
Når to vektorer danner en trekant eller et parallelogram, kan modulet og retningen af den resulterende vektor bestemmes ved hjælp af lovgivningen om sinus og cosinus. Således er modulet for den resulterende vektor, der anvender cosinusloven og ved trekantsmetoden, givet ved:
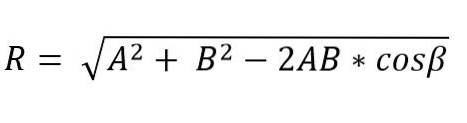
I denne formel er β vinklen modsat siden R, og den er lig med 180º - Ɵ.
I stedet for ved den parallelleogrammetode er modulet for den resulterende vektor:
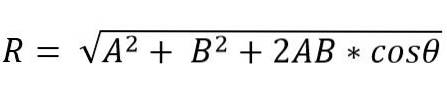
Retningen af den resulterende vektor er givet af vinklen (α), som danner den resulterende med en af vektorerne.
Ved hjælp af sinusloven kan tilføjelse eller subtraktion af vektorer også ske ved hjælp af trekanten eller parallelogrammetoden, velvidende at siderne i hver trekant er proportionale med vinklerne:
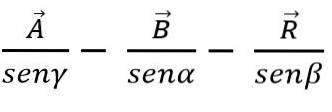
Vektor metode
Dette kan gøres på to måder: afhængigt af dets rektangulære koordinater eller dets basisvektorer.
Det kan gøres ved at oversætte de vektorer, der skal tilføjes eller trækkes mod koordinaternes oprindelse, og derefter alle fremspringene på hver af akserne for planet (x, y) eller mellemrum (x og Z); endelig tilføjes dets komponenter algebraisk. Så for flyet er det:
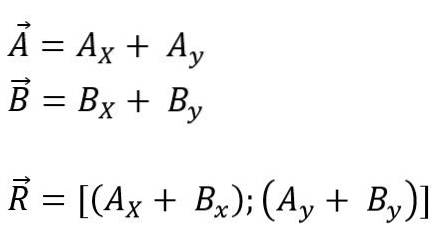
Modulet for den resulterende vektor er:
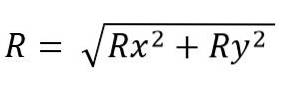
Mens det er plads:
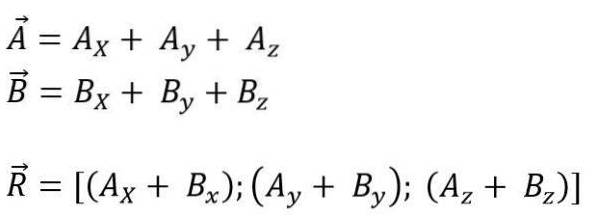
Modulet for den resulterende vektor er:
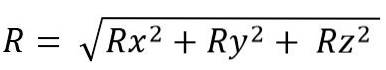
Når vektorsummer udføres, anvendes flere egenskaber, som er:
- Associerende egenskab: den resulterende ændres ikke, når der først tilføjes to vektorer og derefter tilføjes en tredje vektor.
- Kommutativ egenskab: vektorernes rækkefølge ændrer ikke den resulterende.
- Vektordistribuerende egenskab: Hvis en skalar ganges med summen af to vektorer, er den lig med multiplikationen af skalaren med hver vektor.
- Skalærfordelingsegenskab: Hvis en vektor ganges med summen af to skalarer, er den lig med multiplikationen af vektoren for hver skalar.
Multiplikation af vektorer
Multiplikation eller produkt af vektorer kunne gøres som addition eller subtraktion, men at gøre det på den måde mister den fysiske betydning og findes næsten aldrig i applikationer. Derfor er de mest anvendte produkttyper generelt skalar- og vektorproduktet.
Scalar produkt
Det er også kendt som prikproduktet fra to vektorer. Når modulerne i to vektorer ganges med cosinus med den mindste vinkel dannet mellem dem, opnås en skalar. For at udtrykke et skalarprodukt mellem to vektorer placeres et punkt mellem dem, og dette kan defineres som:
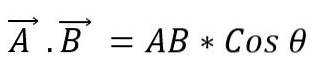
Værdien af den vinkel, der findes mellem de to vektorer, vil afhænge af, om de er parallelle eller vinkelrette; således skal du:
- Hvis vektorerne er parallelle og har samme sans, er cosinus 0º = 1.
- Hvis vektorerne er parallelle og har modsatte retninger, er cosinus 180º = -1.
- Hvis vektorerne er vinkelrette, er cosinus 90º = 0.
Denne vinkel kan også beregnes ved at vide, at:

Prikproduktet har følgende egenskaber:
- Kommutativ egenskab: vektorernes rækkefølge ændrer ikke skalæren.
-Distributive egenskab: hvis en skalar ganges med summen af to vektorer, er den lig med multiplikationen af skalaren med hver vektor.
Vektor produkt
Vektormultiplikation eller krydsprodukt af to vektorer A og B vil resultere i en ny vektor C og udtrykkes ved hjælp af et kryds mellem vektorerne:
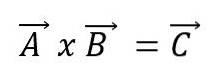
Den nye vektor vil have sine egne egenskaber. Den vej:
- Retningen: denne nye vektor vil være vinkelret på planet, som bestemmes af de originale vektorer.
- Retningen: dette bestemmes med højre håndregel, hvor vektor A drejes mod B, hvilket angiver rotationsretningen med fingrene, og retning af vektoren er markeret med tommelfingeren.
- Modulet: bestemmes af multiplikationen af modulerne til vektorerne AxB, ved sinus af den mindste vinkel, der findes mellem disse vektorer. Det udtrykkes:
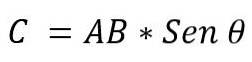
Værdien af den vinkel, der findes mellem de to vektorer, afhænger af, om de er parallelle eller vinkelrette. Så det er muligt at angive følgende:
- Hvis vektorerne er parallelle og har samme forstand, er sinus 0º = 0.
- Hvis vektorerne er parallelle og har modsatte retninger, er sinus 180º = 0.
- Hvis vektorerne er vinkelrette, er sinus 90º = 1.
Når et vektorprodukt udtrykkes som en funktion af dets basisvektorer, har vi:
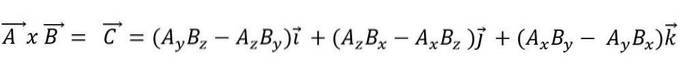
Prikproduktet har følgende egenskaber:
- Det er ikke kommutativt: rækkefølgen af vektorerne ændrer den skalære.
- Distributive egenskab: hvis en skalar ganges med summen af to vektorer, er den lig med multiplikationen af skalaren med hver vektor.
Referencer
- Altman Naomi, M. K. (2015). "Enkel lineær regression." Naturmetoder .
- Angel, A. R. (2007). Elementær algebra. Pearson Uddannelse,.
- Arthur Goodman, L. H. (1996). Algebra og trigonometri med analytisk geometri. Pearson Uddannelse.
- Gusiatnikov, P., & Reznichenko, S. (s.f.). Vektoralgebra i eksempler. Moskva: Mir.
- Lay, D.C. (2007). Lineær algebra og dens anvendelser. Pearson Uddannelse.
- Llinares, J. F. (2009). Lineær algebra: Vektorplads. Euklidisk vektor plads. Alicante Universitet.
- Mora, J. F. (2014). Lineær algebra. Fædreland.


Endnu ingen kommentarer