Vinkelrette linieegenskaber, eksempler, øvelser

EN vinkelret linje Det er en, der danner en vinkel på 90 ° i forhold til en anden linje, kurve eller overflade. Bemærk, at når to linjer er vinkelrette og er på samme plan, når de skærer hinanden, danner de fire identiske vinkler, hver på 90º.

Hvis en af ​​vinklerne ikke er 90º, siges linjerne at være skrå. Vinkelrette linjer er almindelige i design, arkitektur og konstruktion, for eksempel netværket af rør i det følgende billede.

Orienteringen af ​​de vinkelrette linjer kan være forskellig, såsom dem, der er vist nedenfor:

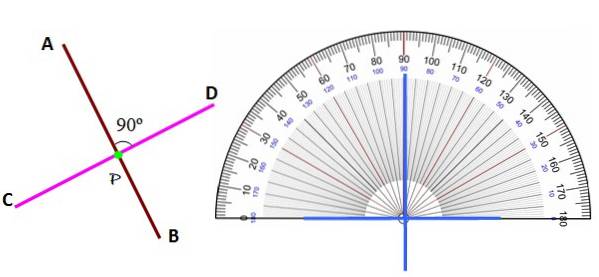
Uanset position genkendes linjerne vinkelret på hinanden ved at identificere vinklen mellem dem som 90º ved hjælp af vinkelmåler.

Bemærk, at i modsætning til parallelle linjer i planet, som aldrig krydser hinanden, gør vinkelrette linjer det altid ved et punkt P, kaldet fod af en af ​​linjerne over den anden. Derfor er der også to vinkelrette linjer pletter.

Enhver linje har uendelige perpendikularer til den, da bare ved at flytte segment AB til venstre eller højre over segment CD, vil vi have nye perpendikularer med en anden fod.

Imidlertid kaldes den vinkelrette, der passerer lige gennem midtpunktet i et segment bisector af nævnte segment.

Artikelindeks

• 1 Eksempler på vinkelrette linjer
  • 1.1 Flere eksempler på vinkelrette linjer
• 2 Øvelser
  • 2.1 - Øvelse 1
  • 2.2 - Øvelse 2
• 3 Referencer

Eksempler på vinkelrette linjer

Vinkelrette linjer er almindelige i bylandskabet. På det følgende billede (figur 3) er der kun fremhævet nogle få af de mange vinkelrette linjer, der kan ses i den enkle facade af denne bygning og dens elementer som døre, kanaler, trin og mere:

Det gode er, at tre linjer vinkelret på hinanden hjælper os med at bestemme placeringen af ​​punkter og objekter i rummet. De er koordinatakserne identificeret som X-akse, Akse y Y z-aksen, tydeligt synligt i hjørnet af et rektangulært rum som det nedenunder:

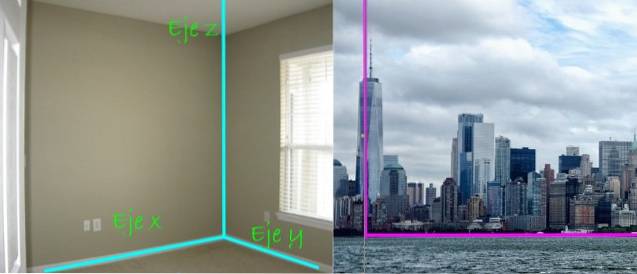
I panoramaudsigten over byen, til højre, er vinkelretningen mellem skyskraberen og jorden også mærkbar. Den første, vil vi sige, findes langs z-aksen, mens jorden er et plan, som i dette tilfælde er planet xy.

Hvis jorden udgør flyet xy, skyskraberen er også vinkelret på enhver gade eller gade, hvilket garanterer dens stabilitet, da en skrånende struktur er ustabil.

Og i gaderne, hvor som helst der er rektangulære hjørner, er der vinkelrette linjer. Mange gader og gader har et lodret layout, så længe terrænet og de geografiske træk tillader det..

For kort at udtrykke vinkelretheden mellem linjer, segmenter eller vektorer anvendes symbolet ⊥. For eksempel hvis linjen L₁ er vinkelret på linjen L_to, vi skrev:

L₁ ⊥ L_to

Flere eksempler på vinkelrette linjer

- I designet er de vinkelrette linjer meget til stede, da mange almindelige objekter er baseret på firkanter og rektangler. Disse firkanter er karakteriseret ved at have indre vinkler på 90º, fordi deres sider er parallelle to og to:

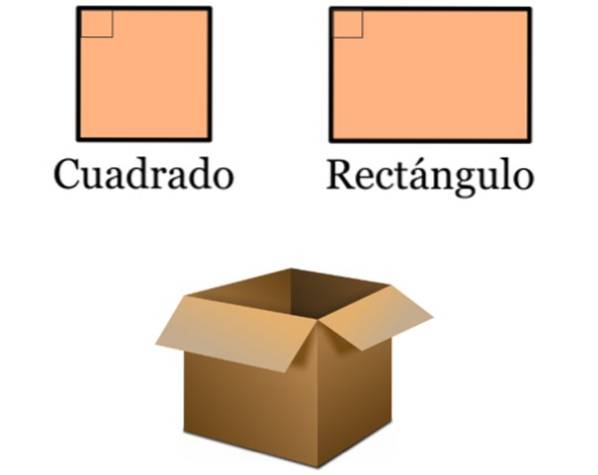
- Markerne, hvor forskellige sportsgrene praktiseres, er afgrænset af mange firkanter og rektangler. Disse indeholder igen vinkelrette linjer.

- To af de segmenter, der udgør en højre trekant, er vinkelret på hinanden. Disse kaldes ben, mens den resterende linje kaldes hypotenus.

- Linjerne i den elektriske feltvektor er vinkelrette på overfladen af ​​en leder i elektrostatisk ligevægt.

- For en ladet leder er potentialudligningslinjerne og overfladerne altid vinkelrette på det elektriske felt.

- I rør- eller ledningssystemer, der bruges til at transportere forskellige typer væsker, såsom gas vist i figur 1, er vinkelrette albuer almindelige. Derfor danner de vinkelrette linjer, sådan er det med et kedelrum:

Uddannelse

- Øvelse 1

Tegn to lodrette linjer ved hjælp af en lineal og et kompas.

Opløsning

Det er meget simpelt at gøre ved at følge disse trin:

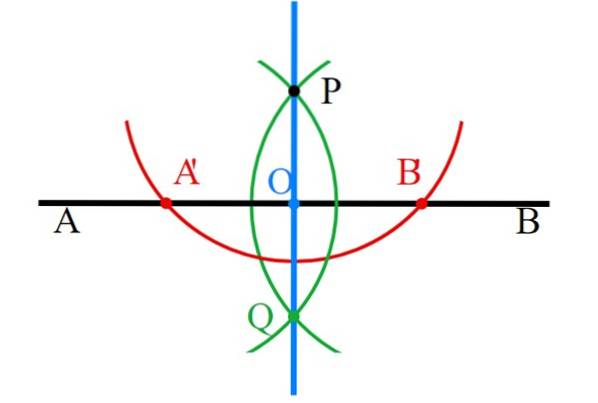
-Den første linje er trukket, kaldet AB (sort).

-Ovenfor (eller under, hvis du foretrækker det), markerer AB punkt P, hvorigennem den vinkelrette passerer. Hvis P er lige over (eller under) midten af ​​AB, er den vinkelrette halvdel af segment AB.

-Med kompasset centreret på P tegner du en cirkel, der skærer AB i to punkter, kaldet A 'og B' (rød).

-Kompasset åbnes ved A'P, det er centreret på A ', og der tegnes en cirkel, der passerer gennem P (grøn).

-Gentag det forrige trin, men åbn nu målingen længden af ​​segmentet B'P (grøn). Begge omkredsbuer krydser hinanden ved punkt Q under P og naturligvis ved sidstnævnte.

-Punkterne P og Q er forbundet med linealen, og den lodrette linje (blå) er klar.

-Endelig skal alle hjælpekonstruktioner slettes omhyggeligt og kun efterlades de vinkelrette..

- Øvelse 2

To linjer L₁ og L_to er vinkelrette, hvis deres respektive skråninger m₁ og m_to møde dette forhold:

m₁ = -1 / m_to

Givet linjen y = 5x - 2, find en linje vinkelret på den, og som passerer gennem punktet (-1, 3).

Opløsning

-Find først hældningen på den vinkelrette linje m_⊥, som angivet i erklæringen. Hældningen på den oprindelige linje er m = 5, koefficienten, der ledsager “x”. Derefter:

m_⊥= -1/5

-Derefter er ligningen af ​​den lodrette linie konstrueret og_⊥, erstatter den tidligere fundne værdi:

Y_⊥= -1 / 5x + b

-Derefter bestemmes værdien af ​​b ved hjælp af det punkt, der gives af udsagnet, (-1,3), da den lodrette linie skal passere gennem den:

y = 3

x = -1

Udskiftning:

3 = -1/5 (-1) + b

Løs værdien af ​​b:

b = 3- (1/5) = 14/5

-Endelig er den endelige ligning bygget:

Y_⊥= -1 / 5x + 14/5

Referencer

1. Baldor, A. 2004. Plane- og rumgeometri. Kulturelle publikationer.
2. Clemens, S. 2001. Geometri med applikationer og problemløsning. Addison Wesley.
3. Matematik er sjov. Vinkelrette linjer. Gendannet fra: mathisfun.com.
4. Monterey Institute. Vinkelrette linjer. Gendannet fra: montereyinstitute.org.
5. Wikipedia. Vinkelrette linjer. Gendannet fra: es.wikipedia.org.