
Youngs modulregning, applikationer, eksempler, øvelser
Det Youngs modul o elasticitetsmodul er den konstant, der relaterer træk- eller kompressionsspændingen med den respektive stigning eller fald i længden af objektet, der udsættes for disse kræfter.
Eksterne kræfter, der påføres objekter, kan ikke kun ændre deres bevægelsestilstand, men er også i stand til at ændre deres form eller endda bryde eller knække dem..

Youngs modul bruges til at studere de ændringer, der produceres i et materiale, når en træk- eller kompressionskraft påføres eksternt. Det er meget nyttigt i emner som teknik eller arkitektur.
Modellen skylder sit navn til den britiske videnskabsmand Thomas Young (1773-1829), som var den, der gennemførte undersøgelser af materialer, der foreslog et mål for forskellige materialers stivhed.
Artikelindeks
- 1 Hvad er Youngs model?
- 2 Hvordan beregnes det?
- 2.1 Fra oprindelse til punkt A
- 2.2 Fra A til B
- 2.3 Fra B til C
- 2.4 Fra C
- 2.5 Formler
- 2.6 Ligning til beregning af deformation
- 3 eksempler
- 4 Løst øvelser
- 4.1 Øvelse 1
- 4.2 Øvelse 2
- 5 Om Thomas Young
- 6 Referencer
Hvad er Youngs model?
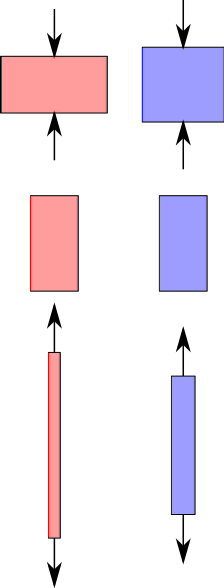
Hvor meget kan et objekt deformeres? Dette er noget, som ingeniører ofte vil vide. Svaret afhænger af materialets egenskaber og de dimensioner, det har.
For eksempel kan du sammenligne to stænger lavet af aluminium med forskellige dimensioner. Hver har et andet tværsnitsareal og længde, og begge udsættes for den samme trækkraft..
Den forventede adfærd vil være følgende:
- Jo større tykkelsen (tværsnittet) af stangen er, jo mindre strækning.
- Jo længere den oprindelige længde er, desto større er den endelige strækning.
Dette giver mening, for trods alt viser erfaringen, at forsøg på at deformere et elastik ikke er det samme som at prøve at gøre det med en stålstang..
En parameter kaldet materialets elasticitetsmodul er en indikation af dets elastiske respons.
Hvordan beregnes det?
Som læge ville Young vide, hvilken rolle arteriernes elasticitet spiller for den gode ydelse af blodcirkulationen. Fra sine erfaringer konkluderede han følgende empiriske forhold:
Spændingen er proportional med deformationen, så længe materialets elastiske grænse ikke overskrides.
Det er muligt grafisk at repræsentere materialets opførsel, når der påføres en stress, som vist i den følgende figur.
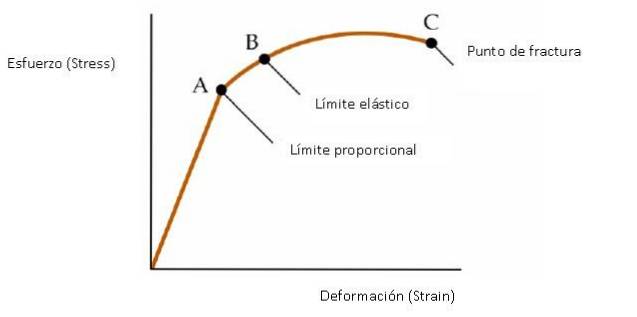
Fra oprindelse til punkt A
I det første afsnit, der går fra oprindelsen til punkt A, er grafen en lige linje. Hookes lov er gyldig der:
F = kx
Hvor F er størrelsen på den kraft, der returnerer materialet til sin oprindelige tilstand, x er den deformation, som den oplever og k er en konstant, der afhænger af genstanden, der udsættes for stress.
De her betragtede deformationer er små, og adfærden er perfekt elastisk..
Fra A til B
Fra A til B opfører materialet sig også elastisk, men forholdet mellem stress og belastning er ikke længere lineært.
Fra B til C
Mellem punkterne B og C gennemgår materialet en permanent deformation, idet det ikke er i stand til at vende tilbage til sin oprindelige tilstand.
Fra C
Hvis materialet fortsætter med at strække sig fra punkt C, bryder det til sidst.
Matematisk kan Youngs observationer opsummeres som følger:
Stress ∝ Stamme
Hvor proportionalitetskonstanten netop er materialets elasticitetsmodul:
Stress = Elasticitetsmodulus x Deformation
Der er mange måder at deformere materialer på. De tre mest almindelige typer stress, som en genstand udsættes for, er:
- Spænding eller strækning.
- Kompression.
- Klip eller forskyd.
En belastning, som materialer ofte udsættes for, for eksempel i civil konstruktion eller bildele, er trækkraft.
Formler
Når et objekt med længden L strækkes eller strækkes, udsættes det for et trækkraft, der forårsager en variation i dets længde. Et diagram over denne situation er repræsenteret i figur 3.
Dette kræver, at der påføres en styrke af størrelsen F pr. Arealeenhed til enderne for at forårsage strækning på en sådan måde, at dens nye længde bliver L + DL.
Den indsats, der gøres for at deformere genstanden, vil være netop denne kraft pr. Arealenhed, mens stamme erfarne er ΔL / L.
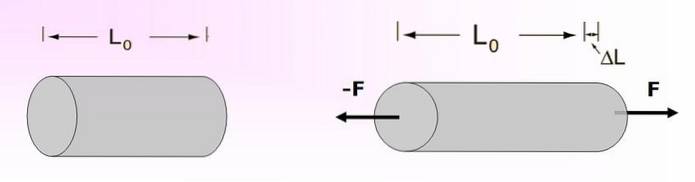
Betegner Youngs modul som Y, og ifølge ovennævnte:
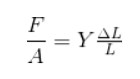
Svaret ligger i, at stammen angiver stammen i forhold til den oprindelige længde. Det er ikke det samme, at en bar på 1 m strækker sig eller krymper 1 cm, en struktur med en længde på 100 meter deformeres også 1 cm.
For at dele og strukturer fungerer korrekt, er der en tolerance med hensyn til de tilladte relative deformationer.
Ligning til beregning af deformation
Hvis ovenstående ligning analyseres som følger:
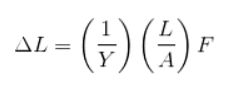
- Jo større tværsnitsareal, jo mindre deformation.
- Jo længere længden er, desto større er deformationen.
- Jo højere Youngs modul, jo lavere er deformationen.
Enheder af stress svarer til newton / kvadratmeter (N / mto). De er også de enheder af pres, som i det internationale system bærer navnet Pascal. Stammen AL / L er derimod dimensionsløs, fordi den er kvotienten mellem to længder.
Enhederne i det engelske system er lb / in.to og de bruges også meget ofte. Konverteringsfaktoren for at gå fra den ene til den anden er: 14,7 lb / in.to = 1,01325 x 105 Pa
Dette fører til, at Youngs modul også har enheder af tryk. Endelig kan ovenstående ligning udtrykkes for at løse Y:
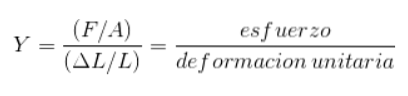
Inden for materialevidenskab er den elastiske reaktion af disse på forskellige bestræbelser vigtig for at vælge den bedst egnede til hver applikation, uanset om den fremstiller en flyvinge eller en billeje. Kendetegnene ved det materiale, der skal bruges, er afgørende for den forventede respons..
For at vælge det bedste materiale er det nødvendigt at kende de bestræbelser, som et bestemt stykke vil blive udsat for; og vælg derfor det materiale, der har de egenskaber, der er mest i tråd med designet.
For eksempel skal et flys vinge være stærk, let og i stand til at bøjes. De anvendte materialer til opførelse af bygninger skal i høj grad modstå seismiske bevægelser, men de skal også have en vis fleksibilitet.
Ingeniører, der designer flyvinger, og også dem, der vælger byggematerialer, skal gøre brug af spændingsbelastningsgrafer som vist i figur 2..
Målinger til bestemmelse af et materiales mest relevante elastiske egenskaber kan udføres i specialiserede laboratorier. Der er således standardiserede tests, som prøverne udsættes for, som forskellige belastninger påføres, og senere måler de resulterende deformationer..
Eksempler
Som allerede nævnt ovenfor, Y afhænger ikke af objektets størrelse eller form, men af materialets egenskaber.
En anden meget vigtig note: for at ligningen ovenfor skal være anvendelig, skal materialet være isotrop, dvs. dets egenskaber skal forblive uændrede i hele dens udvidelse.
Ikke alle materialer er isotrope: der er dem, hvis elastiske respons afhænger af visse retningsbestemte parametre.
Deformationen analyseret i de foregående segmenter er blot en af de mange, som et materiale kan udsættes for. For eksempel med hensyn til kompressionsspænding er det det modsatte af trækspænding.
De angivne ligninger gælder for begge tilfælde og næsten altid værdierne for Y er de samme (isotrope materialer).
En bemærkelsesværdig undtagelse er beton eller cement, der modstår kompression bedre end trækkraft. Derfor skal den forstærkes, når der kræves modstand mod strækning. Stål er det materiale, der er angivet til dette, da det modstår strækning eller trækkraft meget godt..
Eksempler på strukturer udsat for stress inkluderer bygning af søjler og buer, klassiske bygningselementer i mange gamle og moderne civilisationer..

Løst øvelser
Øvelse 1
En 2,0 m lang ståltråd i et musikinstrument har en radius på 0,03 mm. Når kablet er under en spænding på 90 N: hvor meget ændres dets længde?Faktum: Youngs modul af stål er 200 x 109 N / mto
Opløsning
Det er nødvendigt at beregne tværsnitsarealet A = πRto = π. (0,03 x 10-3 m)to = 2,83 x 10-9 mto
Stress er stress pr. Arealenhed:

Da rebet er under spænding, betyder det, at det forlænges.
Den nye længde er L = L.eller + DL, hvor L.eller er den oprindelige længde:
L = 2,32 m
Øvelse 2
En marmorsøjle, hvis tværsnitsareal er 2,0 mto understøtter en masse på 25.000 kg. Finde:
a) Indsatsen i rygsøjlen.
b) Sil.
c) Hvor meget forkortes søjlen, hvis dens højde er 12 m?
Faktum: Youngs marmormodul er 50 x 109 N / mto
Opløsning
a) Indsatsen i søjlen skyldes vægten på 25000 kg:
P = mg = 25000 kg x 9,8 m / sto = 245.000 N
Derfor er indsatsen:
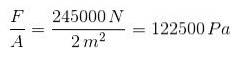
b) Stamme er AL / L:
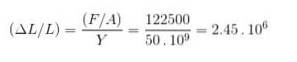
c) ΔL er variationen i længden givet ved:
AL = 2,45 x 10-6 x 12 m = 2,94 x 10-5 m = 0,0294 mm.
Marmorsøjlen forventes ikke at krympe markant. Bemærk, at selvom Youngs modul er lavere i marmor end i stål, og at søjlen også understøtter en meget større kraft, varierer dens længde næsten ikke..
På den anden side er variationen i rebet fra det foregående eksempel meget mere mærkbar, selv om stålet har en meget højere Youngs modul.
Dens store tværsnitsareal griber ind i søjlen, og det er derfor meget mindre deformerbart.
Om Thomas Young

Elasticitetsmodulet er opkaldt efter Thomas Young (1773-1829), en alsidig britisk videnskabsmand, der har ydet store bidrag til videnskaben på mange områder.
Som fysiker studerede Young ikke kun lysets bølgeform, afsløret af det berømte dobbelt slidseksperiment, men han var også læge, sprogforsker og hjalp endda med at dechiffrere en del af de egyptiske hieroglyffer på den berømte Rosetta-sten..
Han var medlem af Royal Society, Royal Swedish Academy of Sciences, American Academy of Arts and Sciences eller det franske videnskabsakademi, blandt andre ædle videnskabelige institutioner..
Det skal dog bemærkes, at konceptet med modellen tidligere blev udviklet af Leonhar Euler (1707-1873), og at forskere som Giordano Riccati (1709-1790) allerede gennemførte et eksperiment, der ville have omsat Youngs model i praksis..
Referencer
- Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 1. Mac Graw Hill. 422-527.
- Giancoli, D. 2006. Fysik: Principper med applikationer. Sjette udgave. Prentice Hall. 238-249.


Endnu ingen kommentarer