Foranstaltninger for central tendens til grupperede dataformler, øvelser

Det trendmål central de angiver værdien omkring hvilken dataene for en distribution er. Det mest kendte er det gennemsnitlige eller aritmetiske gennemsnit, som består i at tilføje alle værdier og dividere resultatet med det samlede antal data.

Men hvis fordelingen består af et stort antal værdier, og de ikke præsenteres ordentligt, er det ikke let at udføre de nødvendige beregninger for at udtrække de værdifulde oplysninger, de indeholder..

Derfor er de grupperet i klasser eller kategorier for at udvikle en distribution af frekvenser. Ved at udføre denne tidligere ordning af data er det så lettere at beregne målene for den centrale tendens, blandt hvilke:

-Halvt

-Median

-mode

-Geometrisk gennemsnit

-Harmonisk middelværdi

Formler

Her er formlerne for målene for den centrale tendens for de grupperede data:

Aritmetisk gennemsnit

Gennemsnittet er det mest anvendte til at karakterisere kvantitative data (numeriske værdier), selvom det er ret følsomt over for de ekstreme værdier i fordelingen. Det beregnes af:

Med:

-X: gennemsnit eller aritmetisk gennemsnit

-F_jeg: klassefrekvens

-m_jeg: klassemærket

-g: antal klasser

-n: samlede data

Median

For at beregne det er det nødvendigt at finde intervallet, der indeholder observationen n / 2 og interpolere for at bestemme den numeriske værdi af observationen ved hjælp af følgende formel:

Hvor:

-c: bredden af ​​det interval, som medianen hører til

-B_M: nedre grænse for intervallet

-F_m: antal observationer indeholdt i intervallet

-n / 2: samlede data divideret med 2.

-F_BM: antal observationer Før af intervallet, der indeholder medianen.

Derfor er medianen et mål for position, det vil sige, den deler datasættet i to dele. De kan også defineres kvartiler, deciler Y percentiler, der deler fordelingen i henholdsvis fire, ti og hundrede dele.

mode

I de samlede data søges den klasse eller kategori, der indeholder flest observationer. Dette er modal klasse. En distribution kan have to eller flere tilstande, i hvilket tilfælde den kaldes bimodal Y multimodal, henholdsvis.

Du kan også beregne tilstanden i grupperede data efter ligningen:

Med:

-L₁: nedre grænse for den klasse, hvor tilstanden findes

-Δ₁: træk mellem frekvensen af ​​den modale klasse og frekvensen af ​​den klasse, der går forud for den.

-Δ_to: trækker mellem modalklassens frekvens og frekvensen for den næste klasse.

-c: bredde på intervallet, der indeholder tilstanden

Harmonisk middelværdi

Det harmoniske gennemsnit betegnes med H. Når du har et sæt af n x-værdier₁, x_to, x₃…, Det harmoniske gennemsnit er det inverse eller gensidige af det aritmetiske gennemsnit af værdiernes omvendte.

Det er lettere at se det gennem formlen:

Og når de grupperede data er tilgængelige, bliver udtrykket:

Hvor:

-H: harmonisk middelværdi

-F_jeg: klassefrekvens

-m_jeg: klassemarkering

-g: antal klasser

-N = f₁ + F_to + F₃ +...

Geometrisk gennemsnit

Hvis de har n positive tal x₁, x_to, x₃…, Dens geometriske gennemsnit G beregnes af produktets ntende rod af alle tallene:

I tilfælde af grupperede data kan det vises, at decimallogaritmen for den geometriske gennemsnitslog G er givet ved:

Hvor:

-G: geometrisk middelværdi

-F_jeg: klassefrekvens

-m_jeg: klassemærket

-g: antal klasser

-N = f₁ + F_to + F₃ +...

Forholdet mellem H, G og X

Det er altid sandt, at:

H ≤ G ≤ X

Mest anvendte definitioner

Følgende definitioner er nødvendige for at finde de værdier, der er beskrevet i formlerne ovenfor:

Frekvens

Frekvens defineres som antallet af gange et stykke data gentages.

Rang

Det er forskellen mellem de højeste og laveste værdier, der er til stede i fordelingen.

Antal klasser

For at vide i hvor mange klasser vi grupperer dataene bruger vi nogle kriterier, for eksempel følgende:

Grænser

De ekstreme værdier for hver klasse eller interval kaldes grænser og hver klasse kan have begge veldefinerede grænser, i hvilket tilfælde den har en lavere og en højere grænse. Eller det kan have åbne grænser, når et interval er givet, for eksempel af værdier, der er større eller mindre end et bestemt antal.

Klassemærke

Det består simpelthen af ​​midtpunktet i intervallet og beregnes ved at beregne et gennemsnit af den øvre og nedre grænse.

Gap bredde

Dataene kan grupperes i klasser af samme eller forskellige størrelse, dette er bredden eller bredden. Den første mulighed er den mest anvendte, da det gør beregningerne meget lettere, selv om det i nogle tilfælde er bydende nødvendigt, at klasserne har forskellige bredder.

Bredden c Intervallet kan bestemmes ved hjælp af følgende formel:

c = Område / N_c

Hvor_c er antallet af klasser.

Træning løst

Nedenfor har vi en række hastighedsmålinger i km / t taget med radar, der svarer til 50 biler, der passerede gennem en gade i en bestemt by:

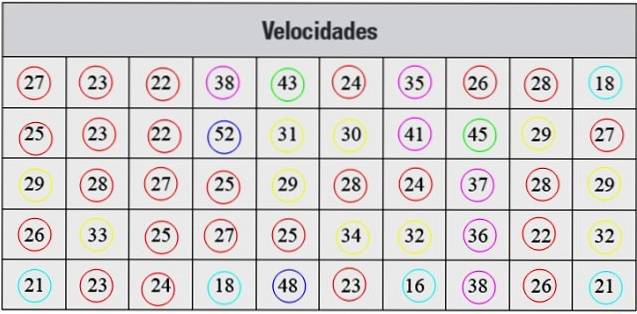
Opløsning

Dataene præsenteret på denne måde er ikke organiseret, så det første skridt er at gruppere dem i klasser.

Trin til gruppering af data og opbygning af tabellen

Trin 1

Find området R:

R = (52 - 16) km / t = 36 km / t

Trin 2

Vælg antallet af klasser N_c, i henhold til de givne kriterier. Da der er 50 data, kan vi vælge N_c = 6.

Trin 3

Beregn bredde c af intervallet:

c = Område / N_c = 36/6 = 6

Trin 4

Formularklasser og gruppedata som følger: for den første klasse vælges en værdi, der er lidt mindre end den laveste værdi, der er til stede i tabellen, som den nedre grænse, så værdien c = 6, tidligere beregnet, føjes til denne værdi opnår den øverste grænse for første klasse.

Vi fortsætter på samme måde med at opbygge resten af ​​klasser, som vist i følgende tabel:

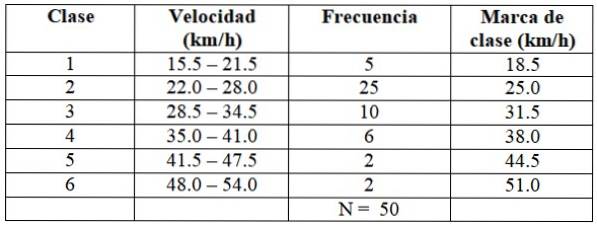
Hver frekvens svarer til en farve i figur 2, på denne måde sikres det, at der ikke tælles nogen værdi..

Beregning af middelværdien

X = (5 x 18,5 +25 x 25,0 + 10 x 31,5 + 6 x 38,0 + 2 x 44,5 + 2 x 51,0) ÷ 50 = 29,03 km / t

Beregning af medianen

Medianen er i klasse 2 i tabellen, da der er de første 30 data for fordelingen.

-Bredden af ​​det interval, som medianen hører til: c = 6

-Nedre grænse for intervallet, hvor medianen er: B_M = 22,0 km / t

-Antal observationer, som intervallet f indeholder_m = 25

-Samlede data divideret med 2: 50/2 = 25

-Antal observationer der er Før af intervallet, der indeholder medianen: f_BM = 5

Og operationen er:

Median = 22,0 + [(25-5) ÷ 25] × 6 = 26,80 km / t

Mode beregning

Mode er også i klasse 2:

-Intervalbredde: c = 6

-Nedre grænse for den klasse, hvor tilstanden findes: L₁ = 22,0

-Træk mellem frekvensen af ​​den modale klasse og frekvensen for den klasse, der går forud for den: Δ₁ = 25-5 = 20

-Træk mellem frekvensen af ​​den modale klasse og frekvensen af ​​den følgende klasse: Δ_to = 25 - 10 = 15

Med disse data er operationen:

Mode = 22,0 + [20 ÷ (20 + 15)] x6 = 25,4 km / t

Beregning af det geometriske gennemsnit

N = f₁ + F_to + F₃ +… = 50

log G = (5 x log 18,5 + 25 x log 25 + 10 x log 31,5 + 6 x log 38 + 2 × log 44,5 + 2 x log 51) / 50 =

log G = 1,44916053

G = 28,13 km / t

Harmonisk gennemsnit beregning

1 / H = (1/50) x [(5 / 18,5) + (25/25) + (10 / 31,5) + (6/38) + (2 / 44,5) + (2/51)] = 0,0366

H = 27,32 km / t

Resumé af målinger af central tendens

Enhederne for variablerne er km / t:

-Gennemsnit: 29.03

-Median: 26.80

-Mode: 25.40

-Geometrisk gennemsnit: 28,13

-Harmonisk gennemsnit: 27.32

Referencer

1. Berenson, M. 1985. Statistik for ledelse og økonomi. Interamericana S.A.
2. Canavos, G. 1988. Sandsynlighed og statistik: Anvendelser og metoder. Mcgraw bakke.
3. Devore, J. 2012. Sandsynlighed og statistik for ingeniørvidenskab og videnskab. 8. plads Udgave. Cengage.
4. Levin, R. 1988. Statistik for administratorer. 2. plads Udgave. Prentice hall.
5. Spiegel, M. 2009. Statistik. Schaum-serien. 4. plads Udgave. Mcgraw bakke.
6. Behandling af grupperede data. Gendannet fra: itchihuahua.edu.mx.
7. Walpole, R. 2007. Sandsynlighed og statistik for ingeniørvidenskab og videnskab. Pearson.