Det vinkelmoment eller vinkelmoment er for rotationsbevægelse, hvad lineært momentum er for translationel bevægelse. Det er en vektormængde, der karakteriserer rotationen af en punktpartikel eller en genstand, der strækker sig omkring en akse, der passerer gennem et punkt.
Dette betyder, at når vinkelmomentet skal beregnes, skal rotationsaksen specificeres korrekt.
Startende med et materielt massepunkt m betegnes vinkelmomentet med L, lineær momentum som s og positionen af partiklen i forhold til en akse, der passerer gennem et bestemt punkt O er r, derefter:
L = r x s
De fedte bogstaver er forbeholdt vektormængder, og korset betyder, at vinkelmomentet er vektorproduktet mellem positionsvektoren r og det lineære øjeblik s af partiklen. Vektoren, der er resultatet af et vektorprodukt, er vinkelret på planet dannet af de deltagende vektorer.
Dette betyder, at retningen og følelsen af L kan findes ved hjælp af højre håndregel for krydsproduktet.
I det internationale system for enheder SI er enhederne med vinkelmoment kg⋅mto/ s, som ikke har et specielt navn. Og for et udvidet legeme, der er sammensat af mange partikler, udvides ovenstående definition bekvemt.
Artikelindeks
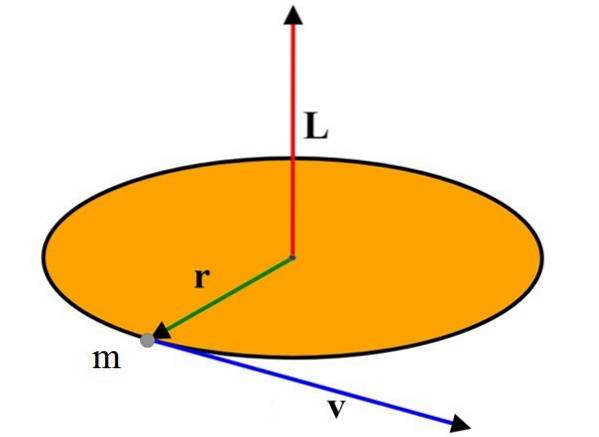
Vinkelmomentvektorens størrelse er i henhold til definitionen af vektorproduktet:
L = r⋅m⋅v⋅sen ϕ = mv (r⋅sen ϕ) = mvℓ
Hvor ϕ er vinklen mellem vektorerne r Y v. Så er ℓ = r sin ϕ den vinkelrette afstand mellem linjen af v og punkt O.
For tilfældet med partiklen, der bevæger sig, og som beskriver omkredsen vist i det øverste billede, er denne vinkel 90 °, da hastigheden altid er tangent til omkredsen og derfor vinkelret på radius..
Derfor er 90 ° = 1 og størrelsen af L det er:
L = m⋅r⋅v
Inertimomentet for et stift legeme beskriver kroppens inerti mod rotation omkring en bestemt akse.
Det afhænger ikke kun af kroppens masse, men også af afstanden til rotationsaksen. Dette er let forståeligt, når du tænker, at det for nogle objekter er lettere at rotere omkring nogle akser end andre..
For et partikelsystem gives inerti-øjeblikket, betegnet med bogstavet I, af:
I = ∑ rjegto Δmjeg
Hvor Δmjeg er en lille portion dej og rjeg er dens afstand fra rotationsaksen. En udvidet krop er sammensat af adskillige partikler, hvorfor dens samlede inertimoment er summen af alle produkterne mellem massen og afstanden, af de partikler, der komponerer den..
Hvis det er en udvidet krop, skifter summeringen til en integral og Δm bliver en massedifferentiale dm. Grænserne for integration afhænger af objektets geometri:
Jeg = ∫M (rto) dm
Begrebet inertimoment er tæt forbundet med vinkelmomentet for et udvidet objekt, som vi vil se nedenfor.
Overvej et system med partikler, der består af masser Δmjeg som roterer efter en omkreds i planet xy, hver har en lineær hastighed relateret til sin vinkelhastighed, sidstnævnte er den samme for alle partikler:
vjeg = ωrjeg
Hvor rjeg er afstanden til rotationsaksen O. Så er størrelsen af vinkelmomentet:
Ljeg = Δmjeg. rjeg. (.rjeg) = rjegtoω Δmjeg
Systemets vinkelmoment vil blive givet af summen:
L = ω ∑ rjegto Δmjeg
Vi identificerer hurtigt inertimomentet som defineret i det foregående afsnit, og derfor er størrelsen af dets vinkelmoment som følger:
L = Iω
Som vi har sagt, at partikelsystemet var i xy-planet, viser det sig, at vinkelmomentet er rettet langs z-aksen, vinkelret på planet. Retningen er givet af drejningens retning: vinkelmomentet er positivt, hvis rotationen udføres mod uret.
En udvidet krop kan opdeles i skiver, hver med vinkelmoment givet af L = Iω rettet langs z-aksen. Hvis objektets symmetriakse falder sammen med z-aksen, er der ikke noget problem, da selv for punkter, der ikke er i xy-planet, annulleres komponenterne i vinkelmomentet vinkelret på denne akse.
Vektorielt:
L = Jegω
Denne ligning er gyldig for tredimensionelle objekter, der roterer omkring en symmetriakse.
Når en nettokraft virker på en partikel eller et legeme, kan dens momentum ændre sig, og følgelig også dets vinkelmoment. For at vide, hvornår det varierer, bruger vi derivatet, som giver os ændringshastigheden over tid, hvis der er en:
Anvendelse af produktreglen for derivatet:
Begrebet v x mv er nul, da det er produktet af en vektor med sig selv, og i det andet sigt finder vi nettokraften F = mtil, Dermed:
Vektorproduktet r x F er intet andet end drejningsmomentet eller nettomomentet, undertiden betegnet med det græske bogstav τ eller som M, altid med fed skrift, da det er en vektormængde. Så analogt med lineært momentum varierer vinkelmomentet, så længe der er et nettomoment eller -moment:
dL/ dt = M
Fra de foregående afsnit har vi set, at:
dL/ dt = M
Det vil sige, at vinkelmomentet varierer, når der er et nettomoment. Hvis der ikke er noget nettomoment, så:
dL/ dt = 0 → L. det er konstant
Med andre ord:
Indledende vinkelmoment = Endelig vinkelmoment
Dette resultat er stadig gyldigt, selv i tilfælde af at et organ ikke er stift, som vi vil se i de følgende eksempler.
Vinkelmoment er en vigtig størrelse, der afsløres i mange situationer, hvilket viser, hvor universel den er:
Når et roterende legeme trækker sig sammen, øges dets rotationshastighed, det er velkendt for skøjteløbere..
Dette skyldes, at når arme og ben trækker sig sammen, mindskes inertimomentet I, da afstanden mellem deres dele falder, men da vinkelmomentet bevares for at holde produktet Iω konstant, skal vinkelhastigheden øges.
Dette gælder ikke kun i skøjteløb, men også i sport og aktiviteter, hvor det er nødvendigt at dreje, såsom dykkere og trapezkunstnere i cirkuset..
Katte lykkes altid at lande på alle fire, når de falder. Selvom de ikke har noget indledende momentum, sørger de for hurtigt at dreje deres ben og hale for at ændre deres rotationsinerti og formår at lande på deres fødder..
Mens de manøvrerer, er deres vinkelmoment ligeledes nul, da deres rotation ikke er kontinuerlig..
En frisbee skal kastes ved at give den et spin, så den flyver, ellers falder den. Faktisk giver vinkelmomentet, der leveres af løfteraket, pucken tilstrækkelig stabilitet til at bevæge sig længere i luften..
Bolde i baseball, fodbold, basketball og andre sportsgrene har vinkelmoment. Da de er sfæriske, har de inerti og roteres under spillet. Siden øjeblikkets inerti er:
I = (2/5) MRto
Hvor M er kuglens masse og R dens radius, er inertimomentet omkring en bestemt (fast) akse:
L = (2/5) MRtoω
Månen bevæger sig væk fra Jorden, da Jordens rotationshastighed falder på grund af friktionen mellem store vandmasser og havbunden.
Jorden-månesystemet bevarer sit vinkelmoment, og hvis Jorden mindsker sit bidrag, øger Månen sit bidrag og bevæger sig væk fra Jorden..
Det første postulat i Bohrs atommodel siger, at en elektron kun optager baner, hvor vinkelmomentet er et heltal multiplum af h / 2π, hvor h er Plancks konstant.
En tynd stålstang har en masse på 500 g og en længde på 30 cm. Den roterer omkring en akse, der passerer gennem dens centrum med en hastighed på 300 omdrejninger pr. Minut. Bestem modulet for dets vinkelmoment.
Vi har brug for inertimomentet for stangen henvist til en akse, der passerer gennem dens centrum. Når man konsulterer tabellerne over inerti finder man, at:
I = (1/12) MLto = (1/12) × 0,5 kg x (30 × 10-to m)to = 3,75 × 10-3 kg.mto
Da det er en udvidet krop, hvor vi kender vinkelhastigheden, bruger vi:
L = Iω
Før vi transformerer vinkelhastigheden eller vinkelfrekvensen ω til radianer / s:
ω = (300 omdrejninger / minut) × (1 minut / 60 sekunder) x (2π radianer / omdrejning) = 10 π rad / s
Udskiftning:
L = 3,75 x 10-3 kg⋅mto × 10 π rad / s = 0,118 kg⋅mto / s
Endnu ingen kommentarer