
Gauss-Seidel metode forklaring, applikationer, eksempler
Det Gauss-Seidel metode er en iterativ procedure til at finde omtrentlige løsninger på et system med lineære algebraiske ligninger med vilkårligt valgt præcision. Metoden anvendes på firkantede matricer med ikke-nul elementer i deres diagonaler, og konvergens er garanteret, hvis matrixen er diagonalt dominerende.
Det blev oprettet af Carl Friedrich Gauss (1777-1855), der gav en privat demonstration til en af sine studerende i 1823. Den blev senere formelt udgivet af Philipp Ludwig von Seidel (1821-1896) i 1874, deraf navnet på begge matematikere..
For en fuldstændig forståelse af metoden er det nødvendigt at vide, at en matrix er diagonalt dominerende, når den absolutte værdi af det diagonale element i hver række er større end eller lig med summen af de absolutte værdier for de andre elementer af den samme række..
Matematisk udtrykkes det således:
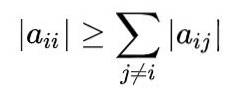
Artikelindeks
- 1 Forklaring ved hjælp af en simpel sag
- 1.1 Skridt, der skal følges
- 1.2 Analyse af metoden
- 2 applikationer
- 3 Eksempler på Gauss-Seidel-metoden
- 3.1 - Eksempel 1
- 3.2 - Eksempel 2
- 3.3 - Eksempel 3
- 3.4 - Eksempel 4
- 4 Referencer
Forklaring ved hjælp af en simpel sag
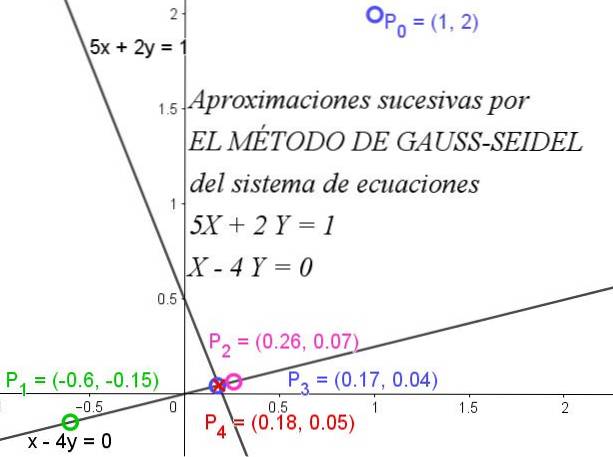
For at illustrere, hvad Gauss-Seidel-metoden består i, tager vi et simpelt tilfælde, hvor værdierne for X og Y kan findes i 2 × 2-systemet med lineære ligninger vist nedenfor:
5X + 2Y = 1
X - 4Y = 0
Trin til at følge
1- For det første er det nødvendigt at afgøre, om konvergensen er sikker. Det bemærkes straks, at det faktisk er et diagonalt dominerende system, da i første række har den første koefficient en højere absolut værdi end de andre i første række:
| 5 |> | 2 |
Ligeledes er den anden koefficient i anden række også diagonalt dominerende:
| -4 |> | 1 |
to- Variablerne X og Y er løst:
X = (1 - 2Y) / 5
Y = X / 4
3- En vilkårlig startværdi placeres, kaldet "frø": Xo = 1, I = 2.
4-Iterationen begynder: for at opnå den første tilnærmelse X1, Y1 erstattes frøet i den første ligning i trin 2 og resultatet i den anden ligning i trin 2:
X1 = (1-2 I) / 5 = (1-2 × 2) / 5 = -3/5
Y1 = X1 / 4 = (-3/5) / 4 = -3/20
5- Vi fortsætter på en lignende måde for at opnå den anden tilnærmelse af løsningen af ligningssystemet:
X2 = (1-2 Y1) / 5 = (1 - 2x (-3/20)) / 5 = 13/50
Y2 = X2 / 4 = (13/50) / 4 = 13/200
6- Tredje iteration:
X3 = (1-2 Y2) / 5 = (1-2 (13/200)) / 5 = 87/500
Y3 = X3 / 4 = (87/500) / 4 = 87/2000
7- Fjerde iteration, som den sidste iteration af denne illustrative sag:
X4 = (1-2 Y3) / 5 = (1-2 (87/2000)) / 5 = 913/5000
Y4 = X4 / 4 = (913/5000) / 4 = 913/20000
Disse værdier stemmer godt overens med den løsning, der findes ved andre opløsningsmetoder. Læseren kan hurtigt kontrollere det ved hjælp af et online matematisk program.
Analyse af metoden
Som det kan ses, i Gauss-Seidel-metoden skal de omtrentlige værdier opnået for den foregående variabel i det samme trin erstattes i den følgende variabel. Dette adskiller det fra andre iterative metoder som Jacobi's, hvor hvert trin kræver tilnærmelser til det foregående trin..
Gauss-Seidel-metoden er ikke en parallel procedure, mens Gauss-Jordan-metoden er. Det er også grunden til, at Gauss-Seidel-metoden har en hurtigere konvergens - i færre trin - end Jordan-metoden..
Hvad angår den diagonalt dominerende matrixtilstand, er dette ikke altid opfyldt. Imidlertid er det i de fleste tilfælde blot tilstrækkeligt at bytte rækkerne fra det originale system til, at betingelsen kan opfyldes. Desuden konvergerer metoden næsten altid, selv når den diagonale dominansbetingelse ikke er opfyldt..
Det tidligere resultat, opnået ved fire gentagelser af Gauss-Seidel-metoden, kan skrives i decimalform:
X4 = 0,1826
Y4 = 0,04565
Den nøjagtige løsning på det foreslåede ligningssystem er:
X = 2/11 = 0,1818
Y = 1/22 = 0,04545.
Så med kun 4 iterationer får du et resultat med en tusindedel præcision (0,001).
Figur 1 illustrerer, hvordan successive iterationer hurtigt konvergerer til den nøjagtige løsning.
Ansøgninger
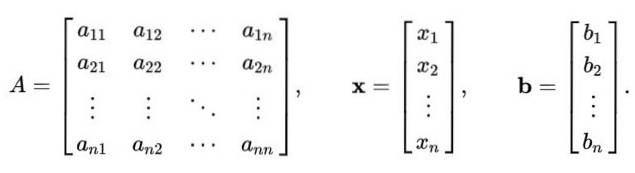
Gauss-Seidel-metoden er ikke kun begrænset til et 2 × 2-system med lineære ligninger. Ovenstående procedure kan generaliseres til løsning af et lineært system af n ligninger med n ukendte, som er repræsenteret i en matrix som denne:
TIL x = b
Hvor TIL er en matrix n x n, Mens x er vektor-n-komponenterne i de n-variabler, der skal beregnes; Y b er en vektor, der indeholder værdierne for de uafhængige termer.
For at generalisere rækkefølgen af iterationer anvendt i det illustrative tilfælde til et n x n-system, hvorfra variablen skal beregnes Xi, følgende formel anvendes:
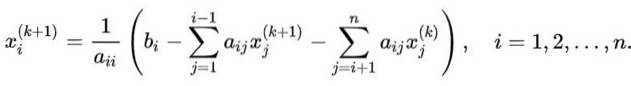
I denne ligning:
- k er indekset for den værdi, der opnås i iterationen k.
-k + 1 angiver den nye værdi i det følgende.
Det endelige antal iterationer bestemmes, når den værdi, der opnås i iterationen k + 1 adskiller sig fra den, der blev opnået umiddelbart før, med en mængde ε, som er nøjagtigt den ønskede præcision.
Eksempler på Gauss-Seidel-metoden
- Eksempel 1
Skriv en generel algoritme for at beregne vektoren af omtrentlige løsninger x af et lineært ligningssystem nxn givet matrixen for koefficienter TIL, vektoren af uafhængige termer b, antallet af iterationer (iter) og vektorens start- eller "frø" -værdi x.
Opløsning
Algoritmen består af to "Til" -cyklusser, den ene for antallet af iterationer og den anden for antallet af variabler. Det ville være som følger:
For k ∊ [1… iter]
For i ∊ [1… n]
X [i]: = (1 / A [i, i]) * (b [i] - ∑j = 1n(A [i, j] * X [j]) + A [i, i] * X [i])
- Eksempel 2
Kontroller funktionen af den tidligere algoritme ved at anvende den i matematisk software SMath Studio gratis at bruge, tilgængelig til Windows og Android. Tag et eksempel på tilfældet med 2 × 2-matrixen, der hjalp os med at illustrere Gauss-Seidel-metoden.
Opløsning

- Eksempel 3
Anvend Gauss-Seidel algoritmen til følgende 3 × 3 ligningssystem, som tidligere er ordnet på en sådan måde, at koefficienterne for diagonalen er dominerende (dvs. større absolut værdi end koefficienternes absolutte værdier af samme række):
9 X1 + 2 X2 - X3 = -2
7 X1 + 8 X2 + 5 X3 = 3
3 X1 + 4 X2 - 10 X3 = 6
Brug nulvektoren som et frø og overvej fem iterationer. Kommenter resultatet.
Opløsning
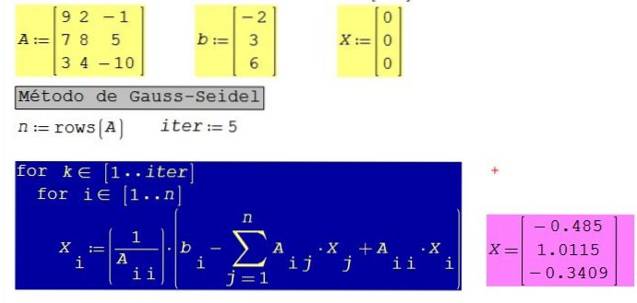
For det samme system med 10 iterationer i stedet for 5 opnås følgende resultater: X1 = -0.485; X2 = 1,0123; X3 = -0,3406
Dette fortæller os, at fem iterationer er nok til at opnå tre decimaler af præcision, og at metoden hurtigt konvergerer til løsningen.
- Eksempel 4
Brug Gauss-Seidel-algoritmen angivet ovenfor, find løsningen på 4 × 4 ligningssystemet nedenfor:
10 x1 - x2 + 2 x3 + 0 x4 = 6
-1 x1 + 11 x2 - 1 x3 + 3 x 4 = 25
2 x1 - 1 x2 + 10 x3 - 1 x4 = -11
0 x1 + 3 x2 - 1 x3 + 8 x4 = 15
For at starte metoden skal du bruge dette frø:
x1 = 0, x2 = 0, x3 = 0 og x4 = 0
Overvej 10 iterationer og estimer fejlen i resultatet sammenlignet med iteration nummer 11.
Opløsning

Når man sammenligner med den næste iteration (nummer 11), er resultatet identisk. De største forskelle mellem de to iterationer er i størrelsesordenen 2 × 10-8, hvilket betyder, at den viste løsning har en præcision på mindst syv decimaler.
Referencer
- Iterative løsningsmetoder. Gauss-Seidel. Gendannet fra: cimat.mx
- Numeriske metoder. Gauss-Seidel. Gendannet fra: test.cua.uam.mx
- Numerisk: Gauss-Seidel metode. Gendannet fra: aprendeenlinea.udea.edu.co
- Wikipedia. Gauss-Seidel metode. Gendannet fra: da. wikipedia.com
- Wikipedia. Gauss-Seidel metode. Gendannet fra: es.wikipedia.com



Endnu ingen kommentarer