
Eksempler på parallelogrammetode, løste øvelser
Det parallelogram metode er en grafisk metode til at tilføje to vektorer i planet. Det bruges ofte til at finde resultatet af to kræfter påført en krop eller med to hastigheder, som i tilfælde af en svømmer, der har til hensigt at krydse en flod vinkelret og afbøjes af strømmen.
For at konstruere parallelogrammet skal oprindelsen af vektorerne, der skal tilføjes, tegnet i skala, falde sammen på et punkt.
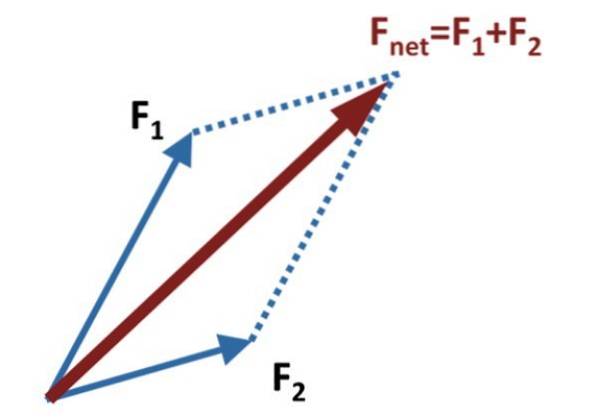
Derefter trækkes hjælpelinjer parallelt med hver vektor og når enden af den anden som vist i figuren ovenfor.
Summen eller den resulterende vektor, også kaldet nettokraften, er vektoren Fnet, som opnås ved at tegne den vektor, der stammer fra den fælles oprindelse for F1 Y Fto, til det punkt, hvor de parallelle hjælpelinjer krydser hinanden. I diagrammet på figuren er disse repræsenteret med stiplede linjer.
Metoden får sit navn fra figuren, der er dannet med addendvektorerne og hjælpelinierne, hvilket netop er et parallelogram. Hoveddiagonalen for parallelogrammet er sumvektoren.
Det er meget vigtigt at bemærke, at rækkefølgen, i hvilken addendvektorerne placeres, ikke ændrer summen overhovedet, da denne operation mellem vektorer er kommutativ.
Artikelindeks
- 1 Eksempel på parallelogrammetoden trin for trin
- 1.1 Særtilfælde: summen af vinkelrette vektorer
- 2 Løst øvelser
- 2.1 - Øvelse 1
- 2.2 - Øvelse 2
- 3 Referencer
Eksempel på parallelogrammetoden trin for trin
Det følgende billede viser vektorerne v Y eller i vilkårlige enheder. Vektoren v måler 3,61 enheder og danner en vinkel på 56,3º med vandret, mens eller måler 6,32 enheder og en vinkel på 18,4 ° i forhold til nævnte referencelinje.
Vi skal finde vektorsummen ved hjælp af parallelogrammetoden.
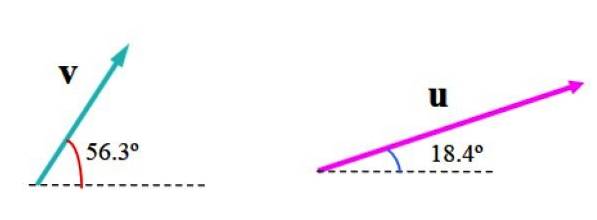
Vælg en passende skala, som den, der er vist i den følgende figur, hvor planet er opdelt med et gitter. Firkantens bredde repræsenterer en (1) enhed.
Da vektorerne ikke ændres, når de oversættes, er de placeret på en sådan måde, at deres oprindelse falder sammen med koordinatsystemets oprindelse (billedet til venstre).
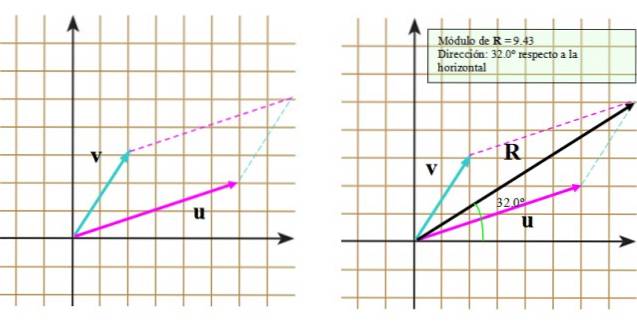
Lad os nu følge disse trin:
- Plot ved slutningen af vektoren v en segmenteret linje, der er parallel med vektoren eller.
- Gentag proceduren, men denne gang med slutningen af vektoren eller.
- Tegn hoveddiagonalen, der strækker sig fra den fælles oprindelse til skæringspunktet for de segmenterede linjer.
Resultatet kan ses i det rigtige billede, hvor den resulterende vektor vises R.
Hvis vi vil vide størrelsen på R, vi kan måle dens længde og sammenligne den med den skala, vi har. Og hvad angår dens retning, kan den vandrette akse eller den lodrette akse f.eks. Bruges som referencer.
Når du bruger den vandrette akse eller x-aksen, skal vinklen R form med nævnte akse måles med vinkelmåler og på denne måde kender vi retningen af R.
Ligeledes størrelsen og retningen af R kan beregnes ved hjælp af cosinus og sinus sætninger, da det dannede parallelogram kan opdeles i to kongruente trekanter, hvis sider er modulerne for vektorerne eller, v Y R. Se udarbejdet eksempel 1.
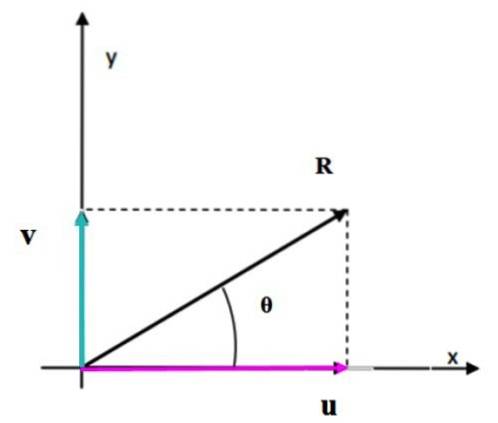
Særtilfælde: summen af vinkelrette vektorer
Når vektorerne er vinkelrette på hinanden, er figuren, der dannes, et rektangel. Modulet for den resulterende vektor svarer til længden af diagonalen, som let kan beregnes ved hjælp af Pythagoras sætning.
Løst øvelser
- Øvelse 1
Vi har vektoren v, der måler 3,61 enheder og danner en vinkel på 56,3º med vandret og vektor eller, hvis mål er 6,32 enheder og danner en vinkel på 18,4º (figur 2). Bestem modulet for den resulterende vektor R = eller + v og retningen, som vektoren danner med den vandrette akse.
Opløsning
Parallelogrammetoden anvendes i overensstemmelse med trinnene beskrevet ovenfor for at opnå vektoren R. Som nævnt før, hvis vektorerne er omhyggeligt tegnet ved at følge skalaen og bruge linealen og vinkelmåleren, skal størrelsen og retningen af R måles direkte på tegningen.
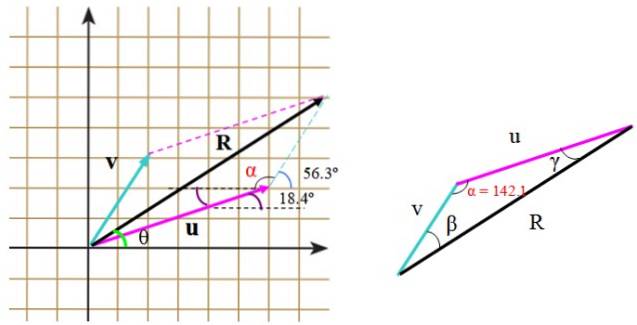
De kan også beregnes direkte ved hjælp af trigonometri og vinklenes egenskaber. Når den dannede trekant ikke er korrekt, som i dette tilfælde, anvendes cosinus sætningen for at finde den manglende side.
I trekanten til højre måler siderne u, v og R. For at anvende cosinus sætningen er det nødvendigt at kende vinklen mellem v Y eller, som vi kan finde ved hjælp af gitteret og placere de vinkler, der er angivet i udsagnet.
Denne vinkel er α og består af:
α = (90-56,3 º) + 90 º + 18,4 º = 142,1 º
Ifølge cosinus sætningen:
Rto = vto + ellerto - 2u⋅v⋅cos α = 3,61to + 6.32to - 2 × 3,61 × 6,32 × cos 142,1º = 88,98
R = 9,43 enheder.
Endelig er vinklen mellem R og den vandrette akse er θ = 18,4 º + γ. Vinklen γ kan findes ved hjælp af sinus sætning:
sin α / R = sin γ / u
Derfor:
sin γ = v (sin α / R) = 3,61 x (sin 142,1º / 9,43)
γ = 13,6º
θ = 18,4 º + 13,6 º = 32 º
- Øvelse 2
En svømmer er ved at krydse en flod, der svømmer vinkelret på strømmen med en konstant hastighed på 2,0 m / s. Svømmeren starter fra A, men ender dog ved B, et punkt nedstrøms på grund af strømmen, der afledte ham.
Hvis strømens hastighed er 0,8 m / s, og alle hastigheder antages konstant, skal du finde svømmerens hastighed set af en observatør, der står på kysten.
Opløsning
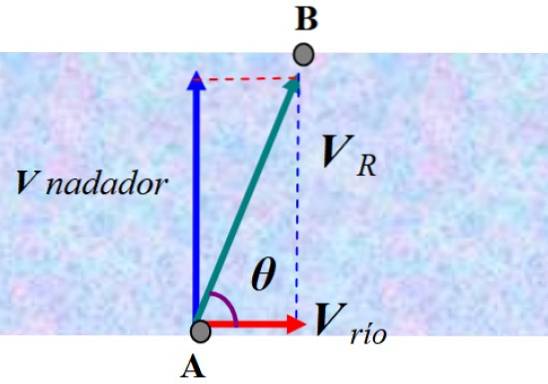
En observatør, der står på kysten, vil se, hvordan svømmeren afbøjes i henhold til den resulterende hastighed VR. For at finde svaret er vi nødt til at tilføje svømmerens hastighed vektorielt i forhold til vandet og strømens hastighed, som vi kalder V flod:
V R = V svømmer + V flod
I figuren, som ikke skaleres, blev vektorerne tilføjet for at opnå V R. I dette tilfælde kan Pythagoras sætning anvendes for at opnå dens størrelse:
VRto = 2,0to + 0,8to = 4,64
VR = 2,15 m / s
Retningen, hvor svømmeren afviger fra den vinkelrette retning, beregnes let og bemærker, at:
θ = arctg (2 / 0,8) = 68,2º
Derefter afviger svømmeren 90º - 68,2º = 27,2º fra sin oprindelige retning.
Referencer
- Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 1. Mc Graw Hill.
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley.
- Figueroa, D. (2005). Serie: Fysik til videnskab og teknik. Bind 1. kinematik. Redigeret af Douglas Figueroa (USB).
- Giambattista, A. 2010. Fysik. 2. plads Ed. McGraw Hill.
- Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14. Red. Bind 1.



Endnu ingen kommentarer