
Indskrevet vinkel på en cirkeldefinition, sætninger, eksempler
Det indskrevet vinkel på en cirkel Det er et, der har sit toppunkt på omkredsen, og dets stråler er secant eller tangent til det. Som en konsekvens vil den indskrevne vinkel altid være konveks eller flad..
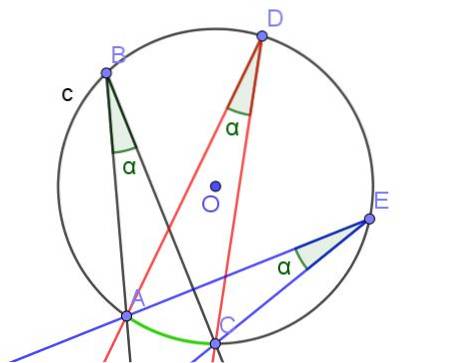
I figur 1 er der angivet flere vinkler indskrevet i deres respektive omkredse. Vinklen ∠EDF er indskrevet ved at have sit toppunkt D på omkredsen og dets to stråler [DE) og [DF) skærer omkredsen.
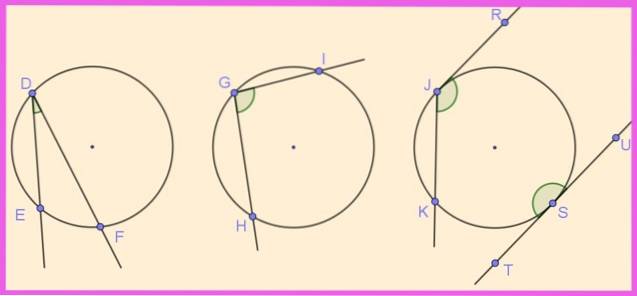
Tilsvarende er vinklen ∠HGI indskrevet, da den har sin toppunkt på omkredsen og dens sider er skille til den.
Vinklerne ∠KJR og ∠UST er også indskrevet på omkredsen. Den første har en sekant side og den anden tangent, mens den anden har sine to sider tangent til omkredsen og danner en plan indskrevet vinkel (180º).
Nogle forfattere kalder den halvindskrevne vinkel, at en af dens sider har tangens til omkredsen, men i denne artikel betragtes den som indskrevet..
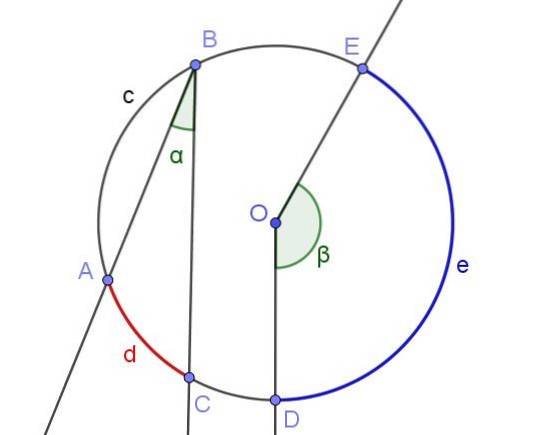
Hver indskrevet vinkel definerer eller undertrykker en bue, der er knyttet til den. For eksempel undertegner den indskrevne vinkel ∠ABC i figur 2 lysbuen A⌒C med længden d.
Den samme figur viser vinklen ∠DOE, som ikke er indskrevet i omkredsen, fordi dens toppunkt ikke har sin omkreds, men i midten O.
Artikelindeks
- 1 Central vinkel
- 2 sætninger
- 2.1 - sætning 1 (indskrevet vinkel og central vinkel)
- 2.2 - sætning 2
- 2.3 - sætning 3
- 3 eksempler
- 3.1 - Eksempel 1
- 3.2 - Eksempel 2
- 4 Referencer
Central vinkel
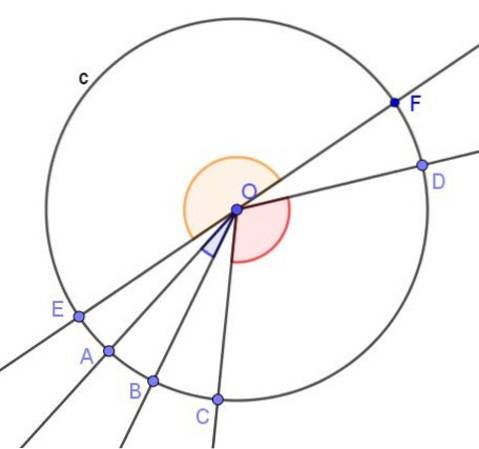
Ud over den indskrevne vinkel, i en omkreds central vinkel, som er den, hvis toppunkt er i midten af omkredsen, og hvis sider skærer omkredsen.
Målingen i radianer af en central vinkel er kvotienten mellem den nedadgående bue, det vil sige buen af omkredsen mellem siderne af vinklen og radius af omkredsen.
Hvis omkredsen er enhed (af radius 1), er længden af buen i de samme radienheder målingen for vinklen i radianer.
Og når vinkelmålingen i grader er påkrævet, multipliceres målingen i radianer med faktoren 180º / π.
Vinkelmåleinstrumenter bruger altid en central vinkel, og lysbuenes længde er direkte kalibreret i grader. Dette betyder, at når en vinkel måles, i baggrunden, hvad der måles, er længden af buen, der er undertrykt af den centrale vinkel.
Sætninger
- Sætning 1 (indskrevet vinkel og central vinkel)
Målene for en indskrevet vinkel er halvdelen af den centrale vinkel, hvis begge vinkler lægger samme bue.
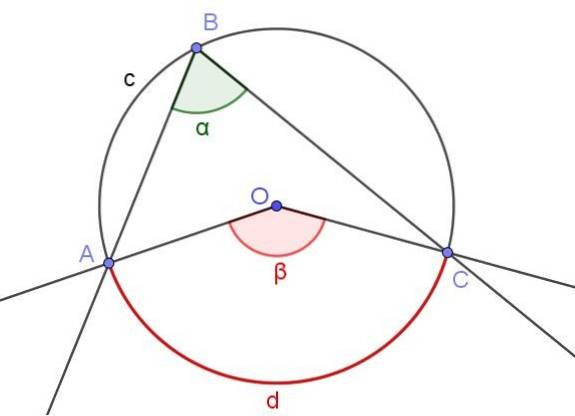
I figur 4 vises to vinkler ∠ABC og ∠AOC, som skærer den samme bue af omkredsen A⌒C.
Hvis målingen for den indskrevne vinkel er α, så er målingen β for den centrale vinkel dobbelt så stor som den indskrevne vinkel (β = 2 α), fordi begge understreger den samme bue af måling d.
Demonstration 1a
For at bevise sætning 1 starter vi med at vise flere særlige tilfælde, indtil vi når det generelle tilfælde.
Antag en indskrevet vinkel, hvor den ene af siderne passerer gennem omkredsen, som vist i figur 5.
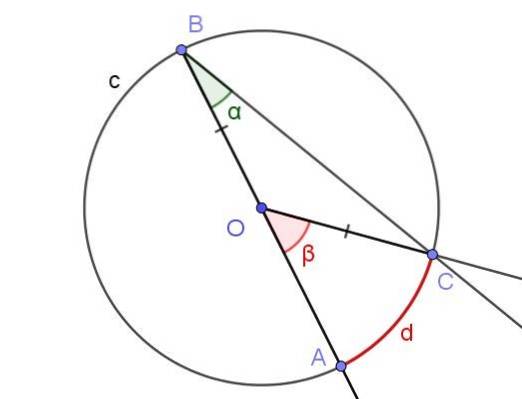
I dette tilfælde dannes den ligebenede trekant COB, da [OC] = [OB].
I en ligebenet trekant er vinklerne ved siden af basen ens, derfor er ∠BCO = ∠ABC = α. På den anden side ∠COB = 180º - β.
I betragtning af summen af de interne vinkler i trekanten COB har vi:
α + α + (180 º - β) = 180 º
Heraf følger, at 2 α = β, eller hvad der er ækvivalent: α = β / 2. Dette falder sammen med, hvad sætning 1 siger: målingen for den indskrevne vinkel er halvdelen af den centrale vinkel, hvis begge vinkler danner samme akkord [AC].
Demonstration 1b
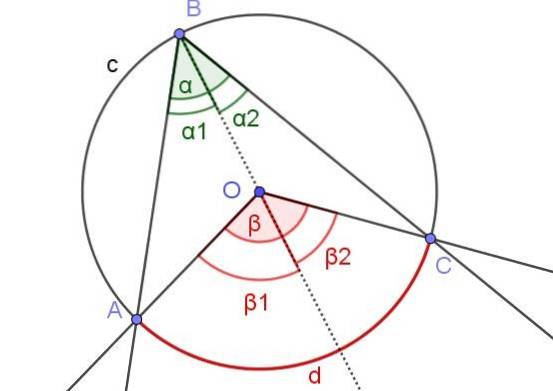
I dette tilfælde har vi en indskrevet vinkel ∠ABC, hvor centrum O af omkredsen er inden for vinklen.
For at bevise sætning 1 i dette tilfælde tegnes hjælpestrålen [BO), så vi har to indskrevne vinkler ∠ABO og ∠OBC ved siden af strålen.
På samme måde har vi de centrale vinkler β1 og βto ved siden af strålen. På denne måde har vi den samme situation som i bevis 1a, så det kan siges, at αto = βto / 2 og α1 = β1 /to. Da α = α1 + ato og β = β1 + βto derfor følger det, at α = α1 + ato = β1 / 2 + βto / 2 = (β1 + βto) / 2 = β / 2.
Afslutningsvis α = β / 2, der opfylder sætning 1.
- Sætning 2
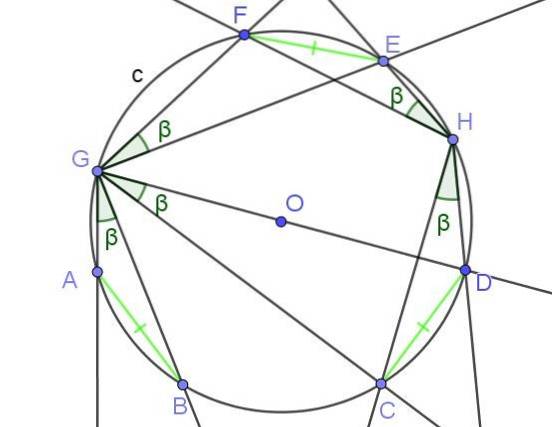
Hvis to eller flere indskrevne vinkler danner samme bue, har de samme mål.
- Sætning 3
De indskrevne vinkler, der underordner akkorder af samme mål, er ens.
Eksempler
- Eksempel 1
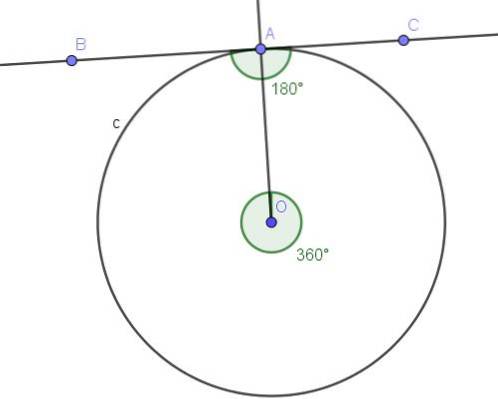
Vis, at den indskrevne vinkel, der understreger diameteren, er en ret vinkel.
Opløsning
Den centrale vinkel ∠AOB forbundet med diameteren er en plan vinkel, hvis mål er 180 º.
Ifølge sætning 1 har hver vinkel, der er indskrevet i omkredsen, der undergraver den samme akkord (i dette tilfælde diameteren), som et mål halvdelen af den centrale vinkel, der undergraver den samme akkord, hvilket for vores eksempel er 180º / 2 = 90º.
- Eksempel 2
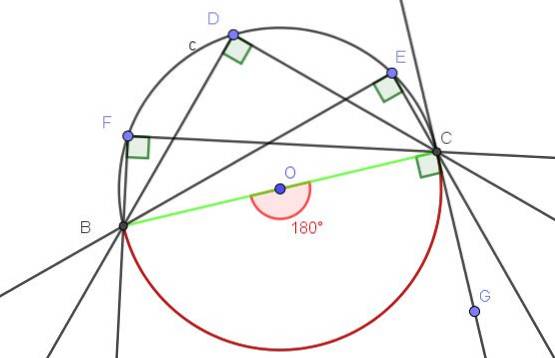
Linjen (BC), der tangerer ved A til omkredsen C, bestemmer den indskrevne vinkel ∠BAC (se figur 10).
Kontroller, at sætningen 1 i de indskrevne vinkler er opfyldt.
Opløsning
Vinklen ∠BAC er indskrevet, fordi dens toppunkt er på omkredsen, og dens sider [AB) og [AC] er tangent til omkredsen, så definitionen af indskrevet vinkel er opfyldt.
På den anden side understreger den indskrevne vinkel ∠BAC buen A, A, som er hele omkredsen. Den centrale vinkel, der lægger buen A⌒A, er en konveks vinkel, hvis mål er den fulde vinkel (360º).
Den indskrevne vinkel, der undergraver hele buen, måler halvdelen af den tilknyttede centrale vinkel, det vil sige ∠BAC = 360º / 2 = 180º.
Med alt det ovenstående bekræftes det, at denne særlige sag opfylder sætning 1.
Referencer
- Baldor. (1973). Geometri og trigonometri. Centralamerikansk kulturredaktion.
- E. A. (2003). Geometrielementer: med kompasets øvelser og geometri. University of Medellin.
- Geometri 1. ESO. Vinkler på omkredsen. Gendannet fra: edu.xunta.es/
- Al videnskab. Foreslåede øvelser af vinkler i omkredsen. Gendannet fra: francesphysics.blogspot.com
- Wikipedia. Indskrevet vinkel. Gendannet fra: es.wikipedia.com



Endnu ingen kommentarer