
Supplerende vinkler, hvilke og hvordan de beregnes, eksempler, øvelser

To eller flere vinkler er komplementære vinkler hvis summen af dens målinger svarer til en ret vinkel. Som det er kendt, er målingen af en ret vinkel i grader 90º, og i radianer er den π / 2.
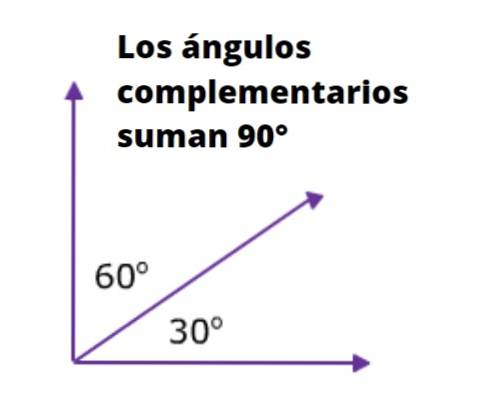
For eksempel er de to vinkler, der støder op til hypotenusen i en ret trekant, komplementære til hinanden, da summen af deres mål er 90 °. Følgende figur er meget illustrativ i denne henseende:
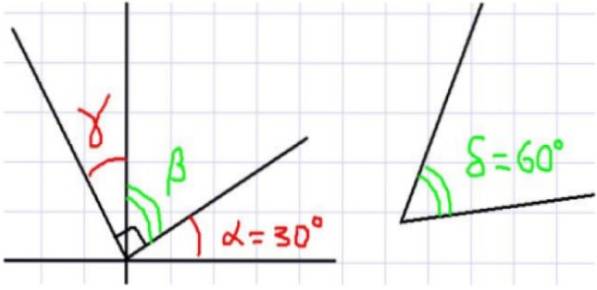
I alt fire vinkler er vist i figur 1. α og β er komplementære, da de er tilstødende og deres sum fuldender en ret vinkel. Tilsvarende er β komplementært til γ, hvorfra det følger, at γ og α har samme mål.
Nu, da summen af α og δ er lig med 90 grader, kan det anføres, at α og δ er komplementære. Da β og δ har den samme komplementære α, kan det endvidere anføres, at β og δ har samme mål.
Artikelindeks
- 1 Eksempler på komplementære vinkler
- 1.1 - Eksempler A, B og C
- 1.2 - Eksempler D, E og F
- 2 Øvelser
- 2.1 - Øvelse 1
- 2.2 - Øvelse 2
- 2.3 - Øvelse 3
- 3 vinkler med vinkelrette sider
- 3.1 Generel regel for vinkelrette sidevinkler
- 4 Referencer
Eksempler på komplementære vinkler
I de følgende eksempler bliver det bedt om at finde de ukendte vinkler markeret med spørgsmålstegn i figur 2.
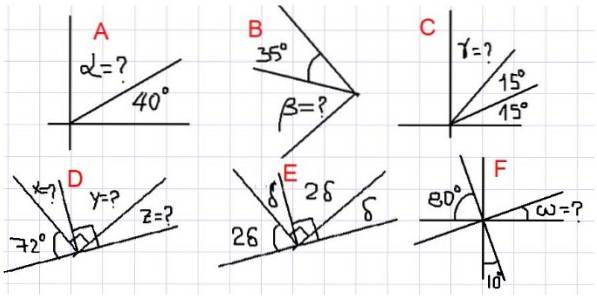
- Eksempler A, B og C
De følgende eksempler er i rækkefølge efter kompleksitet.
Eksempel A
I figuren ovenfor har vi, at de tilstødende vinkler α og 40º tilføjes til en ret vinkel. Det vil sige α + 40º = 90º, derfor α = 90º- 40º = 50º.
Eksempel B
Da β er komplementær til vinklen på 35º, så er β = 90º - 35º = 55º.
Eksempel C
Fra figur 2C har vi, at summen af γ + 15º + 15º = 90º. Med andre ord er γ komplementær til vinklen 30º = 15º + 15º. Så det:
γ = 90 º - 30 º = 60 º
- Eksempler D, E og F
I disse eksempler er der flere vinkler involveret. For at finde de ukendte skal læseren anvende begrebet komplementær vinkel så mange gange som nødvendigt.
Eksempel D
Da X er komplementær til 72º, følger det, at X = 90º - 72º = 18º. Y er komplementær med X, så Y = 90º - 18º = 72º.
Endelig er Z komplementært med Y. Af alt det ovenstående følger, at:
Z = 90º - 72º = 18º
Eksempel E
Vinklerne δ og 2 δ er komplementære, derfor δ + 2 δ = 90 º.
Det vil sige 3δ = 90º, hvilket indebærer at δ = 90º / 3 = 30º.
Eksempel F
Hvis vi kalder vinklen mellem ω og 10 º U, er U supplerende med dem begge, fordi det observeres, at deres sum fuldender en ret vinkel. Heraf følger, at U = 80º. Da U er komplementær med ω, så er ω = 10º.
Uddannelse
Tre øvelser foreslås nedenfor. I dem alle skal værdien af vinklerne A og B i grader findes, så forholdene vist i figur 3 er opfyldt.
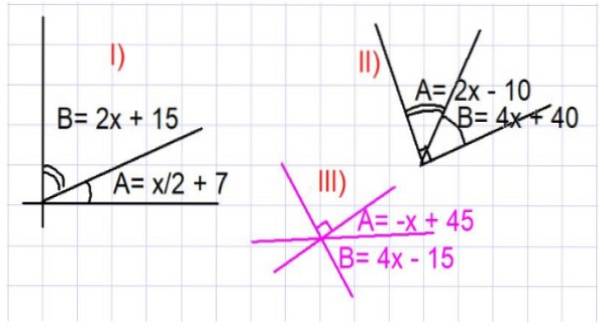
- Øvelse 1
Bestem værdierne for vinklerne A og B fra del I) i figur 3.
Opløsning
Af den viste figur kan det ses, at A og B er komplementære, derfor er A + B = 90º. Vi erstatter udtrykket for A og B som en funktion af x givet i del I):
(x / 2 + 7) + (2x + 15) = 90
Derefter grupperes termerne passende, og der opnås en simpel lineær ligning:
(5x / 2) + 22 = 90
Subtrahere 22 i begge medlemmer har vi:
5x / 2 = 90 -22 = 68
Og endelig er værdien af x ryddet:
x = 2 * 68/5 = 136/5
Nu findes vinklen A ved at erstatte værdien af X:
A = (136/5) / 2 +7 = 103/5 = 20,6 º.
Mens vinkel B er:
B = 2 * 136/5 + 15 = 347 / 5º = 69,4º .
- Øvelse 2
Find værdierne for vinklerne A og B i billede II, figur 3.
Opløsning
Igen, da A og B er komplementære vinkler, har vi: A + B = 90º. Ved at erstatte udtrykket for A og B som en funktion af x givet i del II) i figur 3 har vi:
(2x - 10) + (4x +40) = 90
Lignende vilkår er grupperet sammen for at opnå ligningen:
6 x + 30 = 90
Ved at dele begge medlemmer med 6 får du:
x + 5 = 15
Heraf følger, at x = 10º.
Derfor:
A = 2 * 10 - 10 = 10º
B = 4 * 10 + 40 = 80º.
- Øvelse 3
Bestem værdierne for vinklerne A og B fra del III) i figur 3.
Opløsning
Igen analyseres figuren omhyggeligt for at finde de komplementære vinkler. I dette tilfælde har vi den A + B = 90 grader. Ved at erstatte udtrykket for A og B som en funktion af x givet i figuren har vi:
(-x +45) + (4x -15) = 90
3 x + 30 = 90
At dele begge medlemmer med 3 resultater i følgende:
x + 10 = 30
Fra hvor det følger, at x = 20º.
Med andre ord, vinklen A = -20 +45 = 25º. Og for sin del: B = 4 * 20-15 = 65º.
Vinkelrette sidevinkler
To vinkler siges at være vinkelrette sider hvis hver side har sin tilsvarende vinkelret på den anden. Følgende figur præciserer konceptet:
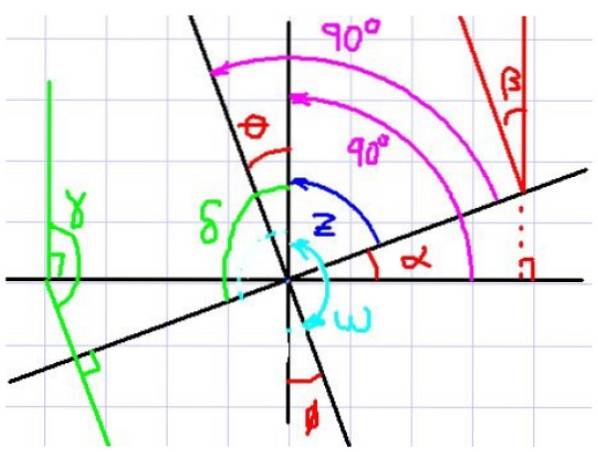
I figur 4 observeres f.eks. Vinklerne α og θ. Bemærk nu, at hver vinkel har sin tilsvarende vinkelret på den anden vinkel.
Det ses også, at α og θ har den samme komplementære vinkel z, derfor konkluderer observatøren straks, at α og θ har samme mål. Det ser ud til, at hvis to vinkler har sider vinkelret på hinanden, er de ens, men lad os se på en anden sag.
Overvej nu vinklerne α og ω. Disse to vinkler har også tilsvarende vinkelrette sider, men de kan ikke siges at være lige store, da den ene er akut og den anden er stump..
Bemærk at ω + θ = 180º. Desuden er θ = α. Hvis du erstatter dette udtryk med z i den første ligning, får du:
δ + α = 180º, hvor δ og α er indbyrdes vinkelrette på sidevinklerne.
Tommelfingerregel for vinkler på vinkelrette sider
Fra ovennævnte kan en regel fastlægges, der er opfyldt, så længe vinklerne har vinkelrette sider:
Hvis to vinkler har indbyrdes vinkelrette sider, er de ens, hvis begge er akutte eller begge er stumpe. Ellers, hvis den ene er akut og den anden er stump, så er de supplerende, dvs. de tilføjer op til 180º.
Anvendelse af denne regel og henvisning til vinklerne i figur 4 kan vi bekræfte følgende:
α = β = θ = φ
y = δ
Med den supplerende vinkel ω af α, β, θ og φ.
Referencer
- Baldor, J. A. 1973. Plane- og rumgeometri. Centralamerikansk kultur.
- Matematiske love og formler. Vinkelmålesystemer. Gendannet fra: ingemecanica.com.
- Wentworth, G. Plane Geometry. Gendannet fra: gutenberg.org.
- Wikipedia. Supplerende vinkler. Gendannet fra: es.wikipedia.com
- Wikipedia. Transportør. Gendannet fra: es.wikipedia.com
- Zapata F. Goniómetro: historie, dele, drift. Gendannet fra: lifeder.com


Endnu ingen kommentarer