
Supplerende vinkler hvad er de, beregning, eksempler, øvelser
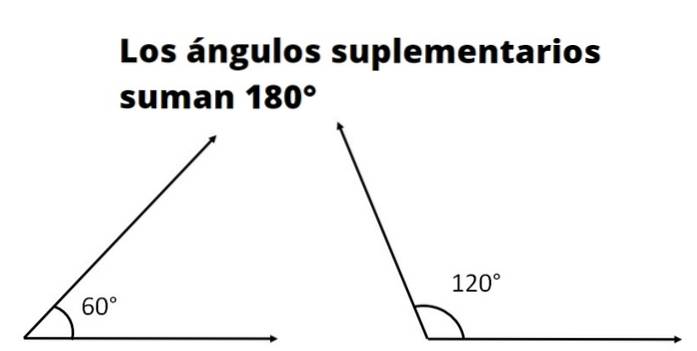
To eller flere er supplerende vinkler hvis summen af dens mål svarer til målingen for en lige vinkel. Målingen af en lige vinkel, også kaldet en plan vinkel, i grader er 180º og i radianer er det π.
For eksempel finder vi, at de tre indvendige vinkler i en trekant er supplerende, da summen af deres mål er 180º. Tre vinkler er vist i figur 1. Af ovenstående følger det, at α og β er supplerende, da de er tilstødende, og deres sum fuldender en lige vinkel.
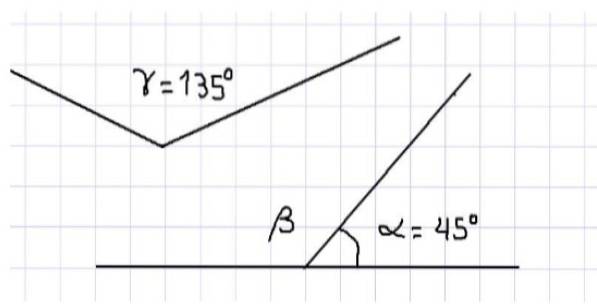
Også i samme figur har vi vinklerne α og γ, som også er supplerende, fordi summen af deres mål er lig med målingen af en plan vinkel, det vil sige 180º. Det kan ikke siges, at vinklerne β og γ er supplerende, fordi, da begge vinkler er stumpe, er deres mål større end 90 º og derfor overstiger deres sum 180 º.
På den anden side kan det siges, at målingen af vinkel β er lig med målingen for vinkel γ, da hvis β er supplerende med α og γ er supplerende med α, så er β = γ = 135º.
Artikelindeks
- 1 Eksempler
- 1.1 Eksempel A
- 1.2 Eksempel B
- 1.3 Eksempel C
- 1.4 Eksempel D
- 1.5 Eksempel E
- 1.6 Eksempel F
- 2 Øvelser
- 2.1 - Øvelse I
- 2.2 - Øvelse II
- 2.3 - Øvelse III
- 3 Supplerende vinkler i to paralleller skåret af en sekant
- 3.1 - Øvelse IV
- 4 Referencer
Eksempler
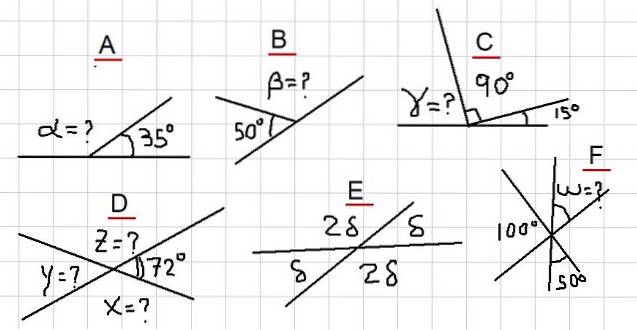
I de følgende eksempler bliver det bedt om at finde de ukendte vinkler, angivet med spørgsmålstegn i figur 2. De spænder fra de enkleste eksempler til nogle lidt mere detaljerede, så læseren skal være mere forsigtig.
Eksempel A
I figuren har vi, at de tilstødende vinkler α og 35 º tilsammen svarer til en plan vinkel. Det vil sige α + 35º = 180º og derfor er det sandt at: α = 180º- 35º = 145º.
Eksempel B
Da β er supplerende med vinklen på 50º, følger det således, at β = 180º - 50º = 130º.
Eksempel C
Fra figur 2C observeres følgende sum: γ + 90º + 15º = 180º. Det vil sige, γ er supplerende med vinklen 105º = 90º + 15º. Det konkluderes derefter, at:
γ = 180 º - 105 º = 75 º
Eksempel D
Da X supplerer 72 °, følger det, at X = 180º - 72º = 108º. Y er Y supplerende med X, så Y = 180º - 108º = 72º.
Og til sidst er Z supplerende med 72º, derfor Z = 180º - 72º = 108º.
Eksempel E
Vinklerne δ og 2 δ er supplerende, derfor δ + 2 δ = 180 º. Hvilket betyder, at 3δ = 180º, og det igen giver os mulighed for at skrive: δ = 180º / 3 = 60º.
Eksempel F
Hvis vi kalder vinklen mellem 100º og 50º U, er U supplerende med dem, fordi det observeres, at deres sum fuldender en plan vinkel.
Det følger straks, at U = 150º. Da U er modsat af toppunktet til W, så er W = U = 150º.
Uddannelse
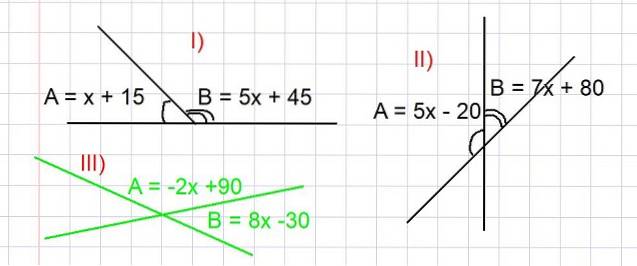
Nedenfor foreslås tre øvelser, hvor værdierne af vinklerne A og B i grader skal findes, således at forholdene vist i figur 3. Opfyldes. Begrebet supplerende vinkler bruges til at løse dem alle..
- Øvelse I
Bestem værdierne for vinklerne A og B fra del I) i figur 3.
Opløsning
A og B er supplerende, hvorfra vi har at A + B = 180 grader, så er udtrykket for A og B erstattet som en funktion af x, som det ser ud på billedet:
(x + 15) + (5x + 45) = 180
En lineær ligning af første orden opnås. For at løse det grupperes termerne straks:
6 x + 60 = 180
Ved at dele begge medlemmer med 6 har vi:
x + 10 = 30
Og endelig løser det, at x er 20º værd.
Nu skal vi tilslutte værdien af x for at finde de ønskede vinkler. Derfor er vinklen A: A = 20 +15 = 35º.
Og for sin del er vinkel B B = 5 * 20 + 45 = 145º.
- Øvelse II
Find værdierne for vinklerne A og B fra del II) i figur 3.
Opløsning
Da A og B er supplerende vinkler, har vi, at A + B = 180 grader. Ved at erstatte udtrykket for A og B som en funktion af x givet i del II) i figur 3 har vi:
(-2x + 90) + (8x - 30) = 180
Igen opnås en første gradsligning, for hvilken begreberne skal grupperes let:
6 x + 60 = 180
Ved at dele begge medlemmer med 6 har vi:
x + 10 = 30
Heraf følger, at x er 20º værd.
Med andre ord, vinklen A = -2 * 20 + 90 = 50º. Mens vinkel B = 8 * 20-30 = 130º.
- Øvelse III
Bestem værdierne for vinklerne A og B fra del III) i figur 3 (i grøn farve).
Opløsning
Da A og B er supplerende vinkler, har vi, at A + B = 180 grader. Vi skal erstatte udtrykket for A og B som en funktion af x givet i figur 3, hvorfra vi har:
(5x - 20) + (7x + 80) = 180
12 x + 60 = 180
Ved at dele begge medlemmer med 12 for at løse værdien af x har vi:
x + 5 = 15
Endelig konstateres det, at x er 10 grader værd.
Nu fortsætter vi med erstatning for at finde vinklen A: A = 5 * 10 -20 = 30º. Og for vinkel B: B = 7 * 10 + 80 = 150º
Supplerende vinkler i to paralleller skåret af en sekant
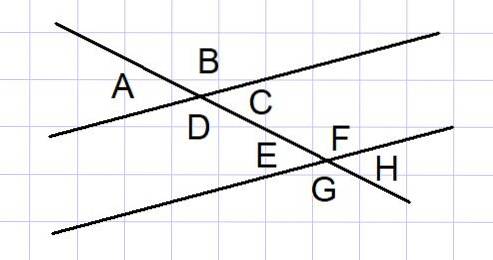
To parallelle linjer skåret af en sekant er en almindelig geometrisk konstruktion i nogle problemer. Mellem sådanne linjer dannes der 8 vinkler som vist i figur 4.
Af disse 8 vinkler er nogle par vinkler supplerende, som vi viser nedenfor:
- De udvendige vinkler A og B og de udvendige vinkler G og H
- De indvendige vinkler D og C og de indvendige vinkler E og F
- De udvendige vinkler A og G og de udvendige vinkler B og H.
- De indvendige vinkler D og E og interiør C og F
For fuldstændighedens skyld er de vinkler, der er lig hinanden, også navngivet:
- De interne skifter: D = F og C = E
- De eksterne veksler: A = H og B = G
- De tilsvarende: A = E og C = H
- Modsætninger efter toppunkt A = C og E = H
- De tilsvarende: B = F og D = G
- Modsætninger efter toppunkt B = D og F = G
- Øvelse IV
Med henvisning til figur 4, som viser vinklerne mellem to parallelle linjer skåret af en sekant, skal du bestemme værdien af alle vinkler i radianer, idet du ved, at vinklen A = π / 6 radianer.
Opløsning
A og B er supplerende ydre vinkler, så B = π - A = π - π / 6 = 5π / 6
A = E = C = H = π / 6
B = F = D = G = 5π / 6
Referencer
- Baldor, J. A. 1973. Plane and Space Geometry. Centralamerikansk kultur.
- Matematiske love og formler. Vinkelmålesystemer. Gendannet fra: ingemecanica.com.
- Wentworth, G. Plane Geometry. Gendannet fra: gutenberg.org.
- Wikipedia. Supplerende vinkler. Gendannet fra: es.wikipedia.com
- Wikipedia. Transportør. Gendannet fra: es.wikipedia.com
- Zapata F. Goniómetro: historie, dele, drift. Gendannet fra: lifeder.com


Endnu ingen kommentarer