Imaginære talegenskaber, applikationer, eksempler

Det imaginære tal er dem, der giver en løsning på ligningen, hvor det ukendte, kvadratisk, er lig med et negativt reelt tal. Den imaginære enhed er i = √ (-1).

I ligningen: z^to= - a, z er et imaginært tal, der udtrykkes som følger:

 z = √ (-a) = i√ (a)

At være til et positivt reelt tal. Ja a = 1, derefter z = i, hvor jeg er den imaginære enhed.

Generelt udtrykkes et rent imaginært tal z altid i form: 

z = y⋅i

Hvor Y er et reelt tal e jeg er den imaginære enhed.

Ligesom reelle tal er repræsenteret på en linje kaldet rigtig lige, på en analog måde er de imaginære tal repræsenteret på imaginær linje.

Det imaginær linje er altid retvinklet (90º form) til rigtig lige og de to linjer definerer et kartesisk plan kaldet komplekst plan.

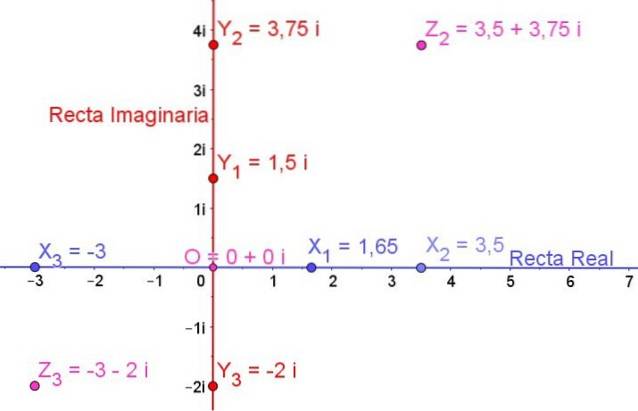
I figur 1 vises det komplekse plan, og på det er nogle reelle tal repræsenteret, nogle imaginære tal og også nogle komplekse tal:

x₁, x_to, x₃ de er reelle tal

Y₁, Y_to, Y₃ de er imaginære tal

Z_to og Z₃ de er komplekse tal

Antallet O er det reelle nul, og det er også det imaginære nul, så oprindelsen O er det komplekse nul udtrykt ved:

0 + 0i 

Artikelindeks

• 1 egenskaber
  • 1.1 Addition og subtraktion af imaginære
  • 1.2 Produkt af forestillinger
  • 1.3 Produkt af et reelt tal af en anden imaginær
  • 1.4 Bemyndigelse af et imaginært
  • 1.5 Summen af ​​et reelt tal og et imaginært tal
• 2 applikationer
• 3 Øvelser med imaginære tal
  • 3.1 - Øvelse 1
  • 3.2 - Øvelse 2
  • 3.3 - Øvelse 3
  • 3.4 - Øvelse 4
  • 3.5 - Øvelse 5
  • 3.6 - Øvelse 6
• 4 Referencer

Ejendomme

Sættet af imaginære tal er betegnet med:

I = …, -3i,…, -2i,…., - i,…., 0i,…., I,…., 2i,…., 3i,…

Og du kan definere nogle operationer på dette numeriske sæt. Der opnås ikke altid et imaginært tal fra disse operationer, så lad os se lidt mere detaljeret på dem:

Addition og subtraktion af imaginære

Imaginære tal kan tilføjes og trækkes fra hinanden, hvilket resulterer i et nyt imaginært tal. For eksempel:

 3i + 2i = 5i

4i - 7i = -3i

Produkt af imaginære

Når produktet fremstilles af et imaginært tal med et andet, er resultatet et reelt tal. Lad os udføre følgende handling for at kontrollere det:

2i x 3i = 6 x i^to = 6 x (√ (-1))^to = 6 x (-1) = -6.

Og som vi kan se, er -6 et reelt tal, skønt det er opnået ved at gange to rene imaginære tal.

Produkt af et reelt tal af en anden imaginær

Hvis et reelt tal ganges med i, bliver resultatet et imaginært tal, der svarer til en 90 graders rotation mod uret.

Og det er, at jeg^to svarer til to på hinanden følgende rotationer på 90 grader, hvilket svarer til at gange med -1, det vil sige i^to = -1. Det kan ses i følgende diagram:

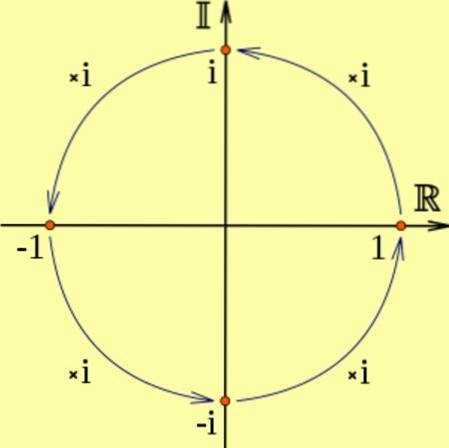
For eksempel:

-3 x 5i = -15i

-3 x i = -3i.

Bemyndigelse af et imaginært

Du kan definere forstærkning af et imaginært tal til et heltal eksponent:

jeg¹ = i

jeg^to = i x i = √ (-1) x √ (-1) = -1

jeg³ = i x i^to = -i

jeg⁴ = i^to x i^to = -1 x -1 = 1

jeg⁵ = i x i⁴ = i

Generelt skal du jegⁿ = i ^ (n mod 4), hvor mod er resten af ​​skillet mellem n Y 4.

Negativ heltalspotensiering kan også udføres:

jeg^-1 = 1 / i¹ = i / (i x i¹) = i / (i^to) = i / (-1) = -i

jeg-^to = 1 / i^to = 1 / (-1) = -1

jeg-³= 1 / i³ = 1 / (- i) = (-1) / i = -1 x i^-1 = (-1) x (-i) = i

Generelt er det imaginære tal b⋅i hævet til magt n:

(b⋅i) iⁿ = bⁿ jegⁿ = bⁿ i ^ (n mod 4)

Nogle eksempler er følgende:

(5 i)¹² = 5¹² jeg¹² = 5¹² jeg⁰ = 5¹² x 1 = 244140625

(5 i)^elleve = 5^elleve jeg^elleve = 5^elleve jeg³ = 5^elleve x (-i) = -48828125 i

(-2 i)¹⁰ = -2¹⁰ jeg¹⁰ = 2¹⁰ jeg^to = 1024 x (-1) = -1024

Summen af ​​et reelt tal og et imaginært tal

Når du tilføjer et reelt tal med et imaginært nummer, er resultatet hverken rigtigt eller imaginært, det er en ny type nummer kaldet komplekst nummer.

For eksempel, hvis X = 3,5 og Y = 3,75i, så er resultatet det komplekse tal:

Z = X + Y = 3,5 + 3,75 i

Bemærk, at i summen kan de reelle og imaginære dele ikke grupperes sammen, så et komplekst tal vil altid have en reel del og en imaginær del..

Denne operation udvider sættet med reelle tal til det bredeste af komplekse tal.

Ansøgninger

Navnet på imaginære tal blev foreslået af den franske matematiker René Descartes (1596-1650) som en hån eller uenighed med forslaget om samme fremsat af den italienske matematiker Raffaelle Bombelli.

Andre store matematikere, såsom Euler og Leibniz, støttede Descartes i denne uenighed og kaldte imaginære tal padder tal, der blev revet mellem at være og intet.

Navnet på imaginære tal forbliver i dag, men deres eksistens og betydning er meget reel og håndgribelig, da de vises naturligt i mange fysiske områder som:

-Relativitetsteorien.

-I elektromagnetisme.

-Kvantemekanik.

Øvelser med imaginære tal

- Øvelse 1

Find løsningerne i følgende ligning:

z^to + 16 = 0

Opløsning

z^to = -16

At tage kvadratrode i begge medlemmer har vi:

√ (z^to ) = √ (-16)

± z = √ (-1 x 16) = √ (-1) √ (16) = i x 4 = 4i

Løsningerne i den oprindelige ligning er med andre ord:

z = + 4i eller z = -4i.

- Øvelse 2

Find resultatet af at hæve den imaginære enhed til magt 5 minus subtraktion af den imaginære enhed hævet til magt -5.

Opløsning

jeg⁵ - jeg-⁵ = i⁵ - 1 / i⁵ = i - 1 / i = i - (i) / (i x i) = i - i / (- 1) = i + i = 2i

- Øvelse 3

Find resultatet af følgende handling:

(3i)³ + 9i 

Opløsning

3³ jeg³ - 9 = 9 (-i) + 9i = -9i + 9i = 0i

- Øvelse 4

Find løsningerne i følgende kvadratiske ligning:

(-2x)^to + 2 = 0

Opløsning

Ligningen omarrangeres som følger:

(-2x)^to = -2

Derefter tages kvadratroden af ​​begge medlemmer

√ ((- 2x)^to) = √ (-2)

± (-2x) = √ (-1 x 2) = √ (-1) √ (2) = i √ (2) = √2 i

Derefter løser vi for x for endelig at opnå:

x = ± √2 / 2 i

Der er to mulige løsninger:

x = (√2 / 2) i

Eller denne anden:

x = - (√2 / 2) i

- Øvelse 5

Find værdien af ​​Z defineret af:

Z = √ (-9) √ (-4) + 7

Opløsning

Vi ved, at kvadratroden af ​​et negativt reelt tal er et imaginært tal, for eksempel er √ (-9) lig med √ (9) x √ (-1) = 3i.

På den anden side er √ (-4) lig med √ (4) x √ (-1) = 2i.

Så den oprindelige ligning kan erstattes af:

3i x 2i - 7 = 6 i^to - 7 = 6 (-1) - 7 = -6 - 7 = -13

- Øvelse 6

Find værdien af ​​Z, der stammer fra følgende opdeling af to komplekse tal:

Z = (9 - i^to) / (3 + i)

Opløsning

Tælleren for udtrykket kan indregnes ved hjælp af følgende egenskab:

En forskel i kvadrater er produktet af summen og forskellen mellem binomierne uden kvadrat.

Derefter:

Z = [(3 - i) (3 + i)] / (3 + i)

Det resulterende udtryk forenkles derefter og forlader

Z = (3 - i)

Referencer

1. Earl, R. Komplekse numre. Gendannet fra: maths.ox.ac.uk.
2. Figuera, J. 2000. Matematik 1.. Diversificeret. CO-BO udgaver.
3. Hoffmann, J. 2005. Valg af emner i matematik. Monfort-publikationer.
4. Jiménez, R. 2008. Algebra. Prentice hall.
5. Wikipedia. Imaginært nummer. Gendannet fra: en.wikipedia.org