
Transcendente tal, hvad er de, formler, eksempler, øvelser
Det transcendente tal er dem, der ikke kan opnås som et resultat af en polynomligning. Det modsatte af et transcendent tal er a algebraisk nummer, der er løsninger af en polynomligning af typen:
tiln xn + tiln-1 xn-1 +… + Ato xto + til1 x + a0 = 0
Hvor koefficienterne an, tiln-1,… tilto, til1, til0 er rationelle tal, kaldet polynomets koefficienter. Hvis et tal x er en løsning på den forrige ligning, er dette tal ikke transcendent.

Vi analyserer et par tal og ser, om de er transcendente eller ej:
a) 3 er ikke transcendent, fordi det er en løsning af x - 3 = 0.
b) -2 kan ikke være transcendent, fordi det er en opløsning af x + 2 = 0.
c) ⅓ er en opløsning af 3x - 1 = 0
d) En opløsning af ligningen xto - 2x + 1 = 0 er √2 -1, så tallet pr. Definition ikke er transcendent.
e) Det er heller ikke √2, fordi det er resultatet af ligningen xto - 2 = 0. Kvadrering √2 giver resultatet 2, der trækkes fra 2 er lig med nul. Så √2 er et irrationelt tal, men det er ikke transcendent.
Artikelindeks
- 1 Hvad er transcendente tal?
- 1.1 Nummeret π
- 1.2 Nummeret e
- 2 Formler, hvor det transcendente tal π vises
- 2.1 Omkredsen af omkredsen
- 2.2 Område af en cirkel
- 2.3 Overflade af en kugle
- 2.4 Kuglens volumen
- 3 Øvelser
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 4 Referencer
Hvad er transcendente tal?
Problemet er, at der ikke er nogen generel regel for at få dem (senere vil vi sige en måde), men nogle af de mest berømte er antallet pi og Neper nummer, betegnet henholdsvis med: π Y og.
Nummeret π
Nummeret π Det ser naturligt ud ved at observere, at den matematiske kvotient mellem omkredsen P af en cirkel og dens diameter D, uanset om det er en lille eller stor cirkel, altid giver det samme nummer, kaldet pi:
π = P / D ≈ 3.14159 ...
Dette betyder, at hvis diameteren af omkredsen tages som måleenheden, for dem alle, store eller små, vil omkredsen altid være P = 3,14… = π, som det kan ses i animationen i figur 2.
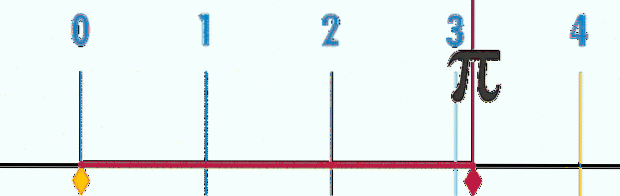
For at bestemme flere decimaler er det nødvendigt at måle P og D med større præcision og derefter beregne kvotienten, hvilket er blevet gjort matematisk. Den nederste linje er, at decimalerne for kvotienten ikke har nogen ende og aldrig gentager sig selv, så tallet π udover at være transcendent er det også irrationel.
Et irrationelt tal er et tal, der ikke kan udtrykkes som delingen af to hele tal.
Det vides, at hvert transcendent tal er irrationelt, men det er ikke sandt, at alle irrationelle tal er transcendente. For eksempel er √2 irrationel, men det er ikke transcendent.
Nummeret e
Det transcendente tal e er basen for naturlige logaritmer, og dets decimale tilnærmelse er:
e ≈ 2.718281828459045235360… .
Hvis du ville skrive nummeret og nøjagtigt ville det være nødvendigt at skrive uendelige decimaler, fordi hvert transcendente tal er irrationelt, som sagt før.
De første ti cifre af og er lette at huske:
2,7 1828 1828, og selv om det ser ud til at følge et gentaget mønster, opnås dette ikke i decimaler af orden større end ni.
En mere formel definition af og er den næste:
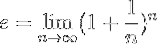
Hvilket betyder, at den nøjagtige værdi af og opnås ved at udføre den operation, der er angivet i denne formel, når det naturlige tal n har tendens til uendelig.
Dette forklarer, hvorfor vi kun kan få tilnærmelser til og, da uanset hvor stort antallet n er placeret, vil det altid være muligt at finde en n højere.
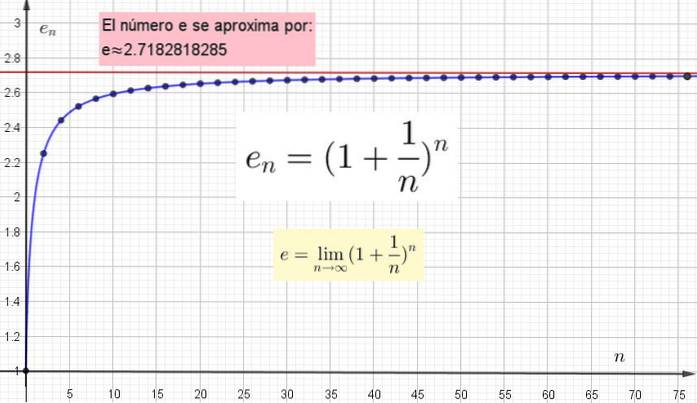
Lad os se på nogle tilnærmelser alene:
-Når n = 100 så (1 + 1/100)100 = 2,70481, som næppe falder sammen i den første decimal med den "sande" værdi af e.
-Hvis du vælger n = 10.000, har du (1 + 1 / 10.000)10.000 = 2.71815, der matcher den "nøjagtige" værdi af e i de første tre decimaler.
Denne proces skal følges uendeligt for at opnå den "sande" værdi af e. Jeg tror ikke, vi har tid til at gøre det, men lad os prøve en mere:
Lad os bruge n = 100.000:
(1 + 1 / 100.000)100.000 = 2.7182682372
Det har kun fire decimaler, der matcher den værdi, der betragtes som nøjagtig.
Det vigtige er at forstå, at jo højere værdien af n er valgt til at beregne en, jo tættere det er på den sande værdi. Men den sande værdi kan kun fås, når n er uendelig.
Andre vigtige tal
Bortset fra disse berømte numre er der andre transcendente tal, for eksempel:
- to√2
Hvert algebraisk tal, bortset fra 0 eller 1, rejst til en irrationel eksponent vil være et transcendent tal.
-Champernowne-nummeret i base 10:
C_10 = 0.123456789101112131415161718192021… .
-Champernowne-nummeret i base 2:
C_2 = 0.1101110010110111… .
-Gamma-nummeret γ eller Euler-Mascheroni-konstanten:
γ ≈ 0,577 215 664 901 532 860 606
Hvilket opnås ved at udføre følgende beregning:
γ ≈ 1 + ½ + ⅓ + ¼ +… + 1 / n - ln (n)
Hvornår n være meget meget stor. For at have den nøjagtige værdi af gammatallet skal du foretage beregningen med n uendelig. Noget svarende til det, vi gjorde ovenfor.
Og der er mange flere transcendente tal. Den store matematiker Georg Cantor, født i Rusland og boede mellem 1845 og 1918, viste, at sættet med transcendente tal er meget større end sættet med algebraiske tal.
Formler, hvor det transcendente tal π vises
Omkredsens omkreds
P = π D = 2 π R, hvor P er omkredsen, D diameteren og R omkredsen. Det skal huskes, at:
-Diameteren af omkredsen er det længste segment, der forbinder to punkter af det samme, og som altid passerer gennem dets centrum,
-Radius er halvdelen af diameteren og er det segment, der går fra midten til kanten.
Område af en cirkel
A = π Rto = ¼ π Dto
Kuglens overflade
S = 4 π Rto.
Ja, selvom det måske ikke ser ud som det, er overfladen af en kugle den samme som for fire cirkler med samme radius som kuglen..
Kuglens volumen
V = 4/3 π R3
Uddannelse
- Øvelse 1
"EXÓTICA" -pizzeriaen sælger pizzaer med tre diametre: små 30 cm, mellemstore 37 cm og store 45 cm. Et barn er meget sultent, og han indså, at to små pizzaer koster det samme som en stor. Hvad der vil være bedre for ham, køb to små pizzaer eller en stor?

Opløsning
Jo større område, jo større mængde pizza, derfor beregnes arealet af en stor pizza og sammenlignes med arealet for to små pizzaer:
Stort pizzaområde = ¼ π Dto = ¼ ⋅3.1416⋅45to = 1590,44 cmto
Lille pizza område = ¼ π dto = ¼ ⋅3.1416⋅30to = 706,86 cmto
Derfor har to små pizzaer et areal på
2 x 706,86 = 1413,72 cmto .
Det er klart: du får mere pizza til at købe en enkelt stor end to små.
- Øvelse 2
Pizzeriaen “EXÓTICA” sælger også en halvkugleformet pizza med en radius på 30 cm til samme pris som en rektangulær form med en side på 30 x 40 cm. Hvilket ville du vælge?

Opløsning
Som nævnt i det foregående afsnit er overfladen af en kugle fire gange så stor som en cirkel med samme diameter, så en halvkugle med en diameter på 30 cm vil have:
12 '' halvkugleformet pizza: 1413,72 cmto (to gange en cirkel med samme diameter)
Rektangulær pizza: (30 cm) x (40 cm) = 1200 cmto .
Den halvkugleformede pizza har et større område.
Referencer
- Fernández J. Nummeret e. Oprindelse og nysgerrighed. Gendannet fra: soymatematicas.com
- Nyd matematik. Eulers nummer. Gendannet fra: gustolasmatematicas.com.
- Figuera, J. 2000. Matematik 1.. Diversificeret. CO-BO udgaver.
- García, M. Antallet e i elementær beregning. Gendannet fra: matematica.ciens.ucv.ve.
- Wikipedia. PI-nummer. Gendannet fra: wikipedia.com
- Wikipedia. Transcendente tal. Gendannet fra: wikipedia.com



Endnu ingen kommentarer