
Sinusbølgeegenskaber, dele, beregning, eksempler
Det sinusbølger De er bølgemønstre, der matematisk kan beskrives af sinus- og cosinusfunktionerne. De beskriver nøjagtigt naturlige begivenheder og tidsvarierende signaler, såsom spændinger genereret af kraftværker og derefter brugt i boliger, industrier og gader.
Elektriske elementer såsom modstande, kondensatorer og induktanser, der er forbundet til sinusformede spændingsindgange, producerer også sinusformede reaktioner. Den matematik, der er brugt i beskrivelsen, er relativt ligetil og er blevet grundigt undersøgt..

Matematikken for sinus- eller sinusformede bølger, som de også er kendt, er for sinus- og cosinusfunktionerne.
Disse er gentagne funktioner, hvilket betyder periodicitet. Begge har samme form, bortset fra at cosinus forskydes til venstre i forhold til sinus med en kvart cyklus. Det kan ses i figur 2:

Derefter cos x = sin (x + π / 2). Ved hjælp af disse funktioner er en sinusbølge repræsenteret. For at gøre dette placeres den pågældende størrelse på den lodrette akse, mens tiden er placeret på den vandrette akse..
Grafen ovenfor viser også den gentagne kvalitet af disse funktioner: mønsteret gentager sig kontinuerligt og regelmæssigt. Takket være disse funktioner er det muligt at udtrykke sinusformede spændinger og strømme varierende i tid og placere dem på den lodrette akse i stedet for Y, -en v eller en jeg til at repræsentere spænding eller strøm og på den vandrette akse i stedet for x, det t vejr.
Den mest generelle måde at udtrykke en sinusbølge på er:
v (t) = vm sen (ωt + φ)
Derefter vil vi dykke ned i betydningen af dette udtryk ved at definere nogle grundlæggende udtryk for at karakterisere sinusbølgen.
Artikelindeks
- 1 dele
- 1.1 Periode
- 1.2 Amplitude
- 1.3 Cyklus
- 1.4 Frekvens
- 1.5 Fase
- 2 Sinusgenerator
- 2.1 Anvendelse af Faradays lov
- 2.2 Wien oscillator
- 3 Sådan beregnes sinusbølger?
- 3.1 Oscilloskopet
- 4 eksempler
- 4.1 Eksempel 1
- 4.2 Eksempel 2
- 5 Referencer
Dele
Periode, amplitude, frekvens, cyklus og fase er begreber anvendt på periodiske eller gentagne bølger og er vigtige for at karakterisere dem korrekt..
Periode
En periodisk funktion som de nævnte, som gentages med regelmæssige intervaller, opfylder altid følgende egenskab:
f (t) = f (t + T) = f (t + 2T) = f (t + 3T) =… .
Hvor T er en mængde kaldet bølge periode, y er den tid det tager at gentage en fase af den samme. I internationale systemenheder måles perioden i sekunder.
Amplitude
I henhold til det generelle udtryk for sinusbølgen v (t) = vm sin (ωt + φ), vm er den maksimale værdi af funktionen, der opstår når sin (ωt + φ) = 1 (husk at den største værdi, som både sinus- og cosinusfunktionerne tillader, er 1). Denne maksimale værdi er netop den bølge amplitude, også kendt som peak amplitude.
I tilfælde af en spænding måles den i volt, og hvis den er en strøm, vil den være i ampere. I den viste sinusbølge er amplituden konstant, men i andre typer bølger kan amplituden variere.
Cyklus
Det er en del af bølgen indeholdt i en periode. I den foregående figur blev perioden taget ved at måle den fra to på hinanden følgende toppe eller kamme, men den kan begynde at måles fra andre punkter i bølgen, så længe de er begrænset af en periode.
Overhold i den følgende figur, hvordan en cyklus dækker fra et punkt til et andet med samme værdi (højde) og samme hældning (hældning).
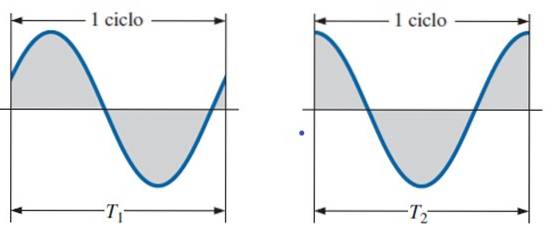
Frekvens
Det er antallet af cyklusser, der forekommer på 1 sekund og er knyttet til argumentet for sinusfunktionen: .t. Frekvensen betegnes som F og måles i cyklusser pr. sekund eller Hertz (Hz) i det internationale system.
Frekvensen er periodens omvendte mængde, derfor:
f = 1 / T
Mens frekvensen F er relateret til vinkelfrekvens ω (pulsering) såsom:
ω = 2πF
Vinkelfrekvensen udtrykkes i radianer / sekund i det internationale system, men radianerne er dimensionsløse, så frekvensen F og vinkelfrekvensen ω de har de samme dimensioner. Bemærk, at produktet .t giver radianer som et resultat og skal tages i betragtning, når du bruger lommeregneren til at opnå værdien af sen ωt.
Fase
Det svarer til den vandrette forskydning, der opleves af bølgen, i forhold til en tid, der tages som reference.
I den følgende figur er den grønne bølge én gang foran den røde bølge td. To sinusbølger er inde fase når dens frekvens og fase er den samme. Hvis fasen adskiller sig, er de i hul. Bølgerne i figur 2 er også ude af fase.
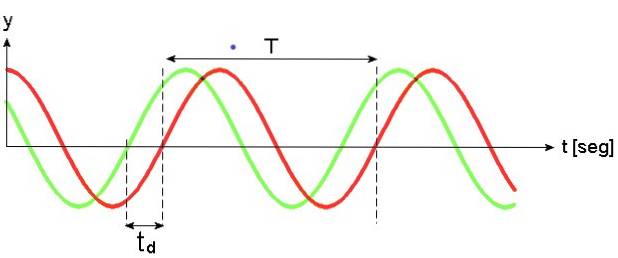
Hvis bølgefrekvensen er forskellig, vil de være i fase, når fasen ωt + φ er den samme i begge bølger på bestemte tidspunkter.
Sinusgenerator
Der er mange måder at få et sinusbølgesignal på. Hjem stikkontakter give dem.
Faradays retshåndhævelse
En ret enkel måde at opnå et sinusformet signal på er at bruge Faradays lov. Dette indikerer, at i et lukket strømkredsløb, for eksempel en sløjfe, der er placeret midt i et magnetfelt, genereres en induceret strøm, når magnetfeltstrømmen gennem den ændrer sig i tid. Derfor er en induceret spænding eller induceret emf.
Fluxen af magnetfeltet varierer, hvis sløjfen roteres med konstant vinkelhastighed midt i feltet skabt mellem N- og S-polen på magneten vist i figuren..
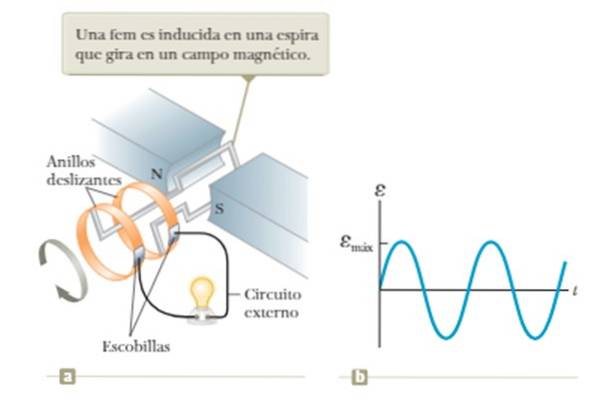
Begrænsningen af denne indretning er afhængigheden af den spænding, der opnås med sløjfens rotationsfrekvens, som det ses mere detaljeret i eksempel 1 i eksemplet nedenfor..
Wien Oscillator
En anden måde at få en sinusbølge, denne gang med elektronik, er via Wien-oscillatoren, som kræver en operationsforstærker i forbindelse med modstande og kondensatorer. På denne måde opnås sinusbølger, hvis frekvens og amplitude brugeren kan ændre alt efter deres bekvemmelighed ved at justere med afbrydere..
Figuren viser en sinusformet signalgenerator, hvormed andre bølgeformer også kan opnås: trekantet og kvadratisk blandt andre..

Sådan beregnes sinusbølger?
For at udføre beregninger, der involverer sinusbølger, anvendes en videnskabelig lommeregner, der har de trigonometriske funktioner sinus og cosinus samt deres inverser. Disse regnemaskiner har tilstande til at arbejde med vinklerne enten i grader eller i radianer, og det er let at konvertere fra den ene form til den anden. Konverteringsfaktoren er:
180 º = π radianer.
Afhængigt af regnemodellen skal du navigere ved hjælp af MODE-tasten for at finde indstillingen GRAD, som giver dig mulighed for at arbejde med de trigonometriske funktioner i grader eller RAD-indstillingen for direkte at arbejde med vinklerne i radianer.
For eksempel sin 25º = 0,4226 med lommeregneren indstillet til DEG-tilstand. Omregning af 25º til radianer giver 0,4363 radianer og sin 0,4363 rad = 0,425889 ≈ 0,4226.
Oscilloskopet
Oscilloskopet er en enhed, der gør det muligt at vise både direkte og alternerende spændings- og strømsignaler på en skærm. Den har drejeknapper til at justere størrelsen på signalet på et gitter som vist i følgende figur:
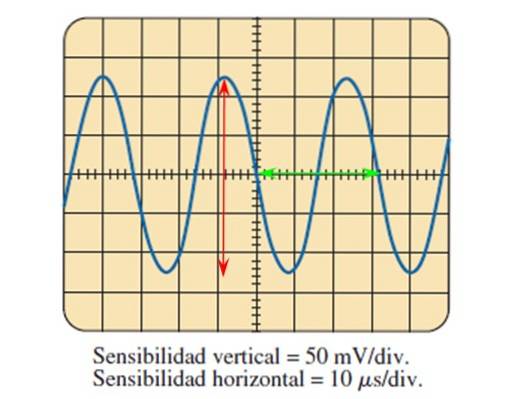
Gennem billedet leveret af oscilloskopet og kendskab til følsomhedsjusteringen i begge akser er det muligt at beregne de bølgeparametre, der tidligere blev beskrevet..
Figuren viser det sinusformede spændingssignal som en funktion af tiden, hvor hver division på den lodrette akse er værd 50 millivolt, mens på den vandrette akse er hver division værd 10 mikrosekunder.
Peak-to-peak amplitude findes ved at tælle de divisioner, som bølgen dækker lodret ved hjælp af den røde pil:
5 divisioner tælles ved hjælp af den røde pil, så spidsen for peak-peak er:
Vpp = 5 divisioner x 50 mV / division = 250 mV.
Maksimal spænding Vs måles fra den vandrette akse, idet den er 125 mV.
For at finde perioden måles en cyklus, for eksempel den, der er afgrænset af den grønne pil, der dækker 3,2 divisioner, så er perioden:
T = 3,2 divisioner x 10 mikrosekunder / division = 32 mikrosekunder = 32 μs
Eksempler
Eksempel 1
For generatoren i fig. 3, viser fra Faradays lov, at den inducerede spænding har en sinusform. Antag at sløjfen består af N drejninger i stedet for kun en, alle med samme område A og roterer med konstant vinkelhastighed ω midt i et magnetfelt B uniform.
Opløsning
Faradays lov siger, at den inducerede emf ε det er:
ε = -N (dΦB / dt)
Hvor ΦB er magnetfeltstrømmen, som vil være variabel, da det afhænger af, hvordan sløjfen udsættes for feltet i hvert øjeblik. Det negative tegn beskriver simpelthen det faktum, at denne emf er imod den årsag, der frembringer den (Lenzs lov). Strømmen på grund af en enkelt drejning er:
ΦB = B.A.cos θ
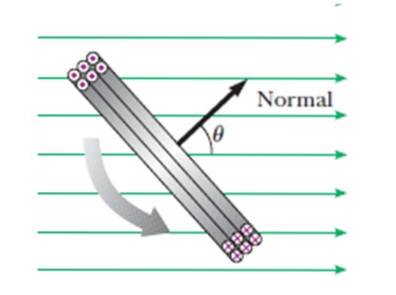
θ er den vinkel, som vektoren er normal i forhold til sløjfens plan, dannes med feltet B Efterhånden som rotation fortsætter (se figur), varierer denne vinkel naturligvis som:
θ = .t
Så det: ΦB = B.A.cos θ = B.A.cos .t. Nu skal vi kun udlede dette udtryk med hensyn til tid, og med dette opnår vi den inducerede emk:
ε = -N.d (B.A.cos ωt) / dt
Ligesom marken B er ensartet, og sløjfens område varierer ikke, de efterlader uden for derivatet:
ε = -NBA. d (cos ωt) / dt = ωNBA. sen .t
Eksempel 2
En sløjfe har et areal på 0,100 mto og roterer ved 60,0 omdrejninger / sek. med sin rotationsakse vinkelret på et ensartet magnetfelt på 0,200 T. Ved at vide, at spolen har 1000 omdrejninger, find: a) Den maksimale emf, der genereres, b) Spolens retning i forhold til magnetfeltet, når den inducerede maksimale emf forekommer.
Opløsning
a) Den maksimale emf er εmaks = ωNBA
Før du fortsætter med at udskifte værdierne, skal frekvensen på 60 omdr./s overføres til internationale systemenheder. Det vides, at 1 omdrejning svarer til en omdrejning eller 2p radianer:
60,0 omdr./s = 120p radianer / s
εmaks = 120p radianer x 1000 omdrejninger x 0,200 T x 0,100 mto = 7539,82 V = 7,5 kV
b) Når denne værdi opstår sen ωt = 1 Dermed:
ωt = θ = 90º,
I et sådant tilfælde er spiralens plan parallel med B, således at vektoren, der er normal for planet, danner 90º med feltet. Dette sker, når vektoren i sort i figur 8 er vinkelret på den grønne vektor, der repræsenterer magnetfeltet.
Referencer
- Boylestad, R. 2011. Introduktion til kredsløbsanalyse. 12. Udgave. Pearson. 327-376.
- Figueroa, D. 2005. Elektromagnetisme. Fysikserie for videnskab og teknik. Bind 6. Redigeret af D. Figueroa. Simon Bolivar University. 115 og 244-245.
- Figueroa, D. 2006. Fysiklaboratorium 2. Redaktionel Equinoccio. 03-1 og 14-1.
- Sinusbølger. Gendannet fra: iessierradeguara.com
- Serway, R. 2008. Fysik til videnskab og teknik. Bind 2. Cengage Learning. 881- 884



Endnu ingen kommentarer