
Endimensionelle bølger matematisk udtryk og eksempler
Det endimensionelle bølger Det er dem, der formerer sig i en enkelt retning, uanset om vibrationen opstår i samme formeringsretning eller ej. Et godt eksempel på dem er bølgen, der bevæger sig gennem en stram streng som en guitar..
I en flad bølge kryds, partiklerne vibrerer i lodret retning (de går op og ned, se den røde pil i figur 1), men den er endimensionel, fordi forstyrrelsen kun bevæger sig i en retning efter den gule pil.

Endimensionelle bølger forekommer ganske ofte i hverdagen. Det følgende afsnit beskriver nogle eksempler på dem og også på bølger, der ikke er endimensionelle, for tydeligt at fastslå forskellene.
Artikelindeks
- 1 Eksempler på endimensionelle bølger og ikke-endimensionelle bølger
- 1.1 En-dimensionelle bølger
- 1.2 Ikke-dimensionelle bølger
- 2 Matematisk udtryk for en endimensionel bølge
- 2.1 En-dimensionel bølgeligning
- 2.2 Arbejdet eksempel
- 3 Referencer
Eksempler på endimensionelle bølger og ikke-dimensionelle bølger
En-dimensionelle bølger
Her er nogle eksempler på endimensionelle bølger, der let kan observeres:
- En lydpuls, der bevæger sig gennem en lige bjælke, da det er en forstyrrelse, der formerer sig hele bjælkens længde.
- En bølge, der bevæger sig gennem en vandkanal, selvom forskydningen af vandoverfladen ikke er parallel med kanalen.
- Bølger, der udbreder sig på en overflade eller gennem et tredimensionelt rum, kan også være endimensionelle, så længe deres bølgefronter er planer parallelle med hinanden og kun bevæger sig i en retning..
Ikke-endimensionelle bølger
Et eksempel på en ikke-dimensionel bølge findes i bølger, der dannes på en stille vandoverflade, når en sten falder ned. Det er en todimensional bølge med en cylindrisk bølgefront.

Et andet eksempel på en ikke-dimensionel bølge er lydbølgen, som en fyrværker genererer ved at eksplodere i en bestemt højde. Dette er en tredimensionel bølge med sfæriske bølgefronter.
Matematisk udtryk for en endimensionel bølge
Den mest generelle måde at udtrykke en endimensionel bølge, der formerer sig uden dæmpning i aksens positive retning x og med hastighed v er matematisk:
y (x, t) = f (x - v.t)
I dette udtryk Y repræsenterer forstyrrelsen i positionen x Med det samme t. Bølgeformen er givet af funktionen F. For eksempel er bølgefunktionen vist i figur 1: y (x, t) = cos (x - v t) og bølgebilledet svarer til øjeblikket t = 0.
En bølge som denne, beskrevet af en cosinus- eller sinusfunktion, kaldes harmonisk bølge. Selv om det ikke er den eneste bølgeform, der findes, er det af største betydning, fordi enhver anden bølge kan repræsenteres som en superposition eller sum af harmoniske bølger. Det handler om det kendte Fourier sætning, så brugt til at beskrive signaler af alle slags.
Når bølgen bevæger sig i den negative retning af x-aksen, ændres den simpelthen v til -v i argument og forlader:
y (x, t) = g (x + v t)
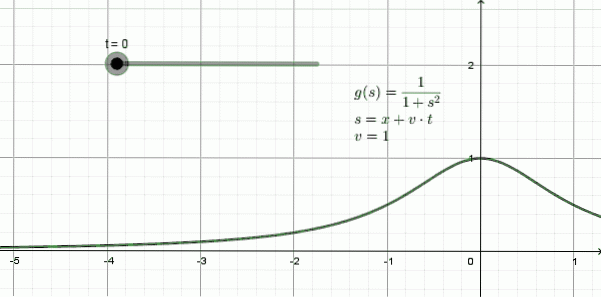
Figur 3 viser animationen af en bølge, der kører til venstre: det er en form, der kaldes en funktion lorentziana og hende matematisk udtryk er:
y (x, t) = 1 / (1 + (x + 1)⋅t)to
I dette eksempel er forplantningshastigheden v = 1, -en enhed af plads for hver tidsenhed-.
En-dimensionel bølgeligning
Bølgeligning er en delvis afledt ligning, hvis opløsning naturligvis er en bølge. Den etablerer det matematiske forhold mellem den rumlige del og den tidsmæssige del af den og har formen:

Arbejdet eksempel
Følgende er det generelle udtryk y (x, t) for en harmonisk bølge:
y (x, t) = A⋅cos (k⋅x ± ω⋅t + θo)
a) Beskriv den fysiske betydning af parametrene A, k, ω Y θo.
b) Hvilken betydning har ± tegnene i cosinusargumentet?
c) Kontroller, at det givne udtryk faktisk er løsningen på bølgeligning fra det foregående afsnit, og find hastigheden v formering.
Løsning til)
Karakteristikken for bølgen findes i følgende parametre:
-TIL repræsenterer amplitude eller "bølgehøjde".
-hvad er der i? bølgenummer og er relateret til bølgelængden λ igennem k = 2π / λ.
-ω er fvinkelfrekvens og er relateret til periode T bølge svingning af
ω = 2π / T.
-θo er indledende fase, som er relateret til startpunktet for bølgen.
Løsning b)
Et negativt tegn tages, hvis bølgen bevæger sig i X-aksens positive retning og ellers et positivt tegn..
Løsning c)
Kontroller, at det givne udtryk er en løsning af bølgeligning er enkel: den delvise afledte af funktionen tages y (x, t) med hensyn til x to gange, delvist afledt med hensyn til t to gange, og kombiner derefter begge resultater for at opnå en ligestilling:
Andet afledt med hensyn til x: ∂toy / ∂xto= -Kto. TIL⋅cos (k⋅x ± ω⋅t + θo)
Andet afledt med hensyn til t: ∂toy / ∂tto= -Ωto. TIL⋅cos (k⋅x ± ω⋅t + θo)
Disse resultater er erstattet i bølgeligning:
-kto. TIL⋅cos (k⋅x ± ω⋅t + θo) = (1 / volto) (-ωto. TIL⋅cos (k⋅x ± ω⋅t + θo))
Så meget TIL som cosinus er forenklet, da de vises på begge sider af lighed og argumentet for cosinus er det samme, reducerer udtrykket derfor til:
-kto = (1 / volto) (-ωto)
Hvilket gør det muligt at opnå en ligning for v med hensyn til ω Y k:
vto = ωto / kto
v = ± ω / k
Referencer
- E-uddannelse. Ligning af endimensionelle harmoniske bølger. Gendannet fra: e-ducativa.catedu.es
- Hjørnet af fysik. Bølgeklasser. Gendannet fra: fisicaparatontos.blogspot.com.
- Figueroa, D. 2006. Waves and Quantum Physics. Serie: Fysik til videnskab og teknik. Redigeret af Douglas Figueroa. Simon Bolivar University. Caracas Venezuela.
- Physics Lab. Bølgebevægelse. Gendannet fra: fisicalab.com.
- Peirce, A. Forelæsning 21: Den endimensionelle bølgeligning: D'Alemberts løsning. Gendannet fra: ubc.ca.
- Bølge ligning. Gendannet fra: en.wikipedia.com



Endnu ingen kommentarer