
Parallelepipede egenskaber, typer, areal, volumen
EN parallelepiped det er et geometrisk legeme dannet af seks flader, hvis hovedkarakteristik er, at alle dets ansigter er parallelogrammer, og også at dets modsatte flader er parallelle med hinanden. Det er en almindelig polyhedron i vores daglige liv, da vi kan finde den i skokasser, form af en mursten, form af en mikrobølgeovn osv..
At være en polyhedron, parallelepiped omslutter et endeligt volumen, og alle dens ansigter er flade. Det er en del af gruppen af prismer, som er de polyeder, hvor alle dens hjørner er indeholdt i to parallelle planer.

Artikelindeks
- 1 Elements of the Parallelepiped
- 1.1 Ansigter
- 1.2 Kanter
- 1.3 Hvirvel
- 1.4 Diagonal
- 1.5 Center
- 2 Karakteristika for Parallelepiped
- 3 typer
- 3.1 Beregning af diagonaler
- 4 Område
- 4.1 Område for en ortohedron
- 4.2 Areal af en terning
- 4.3 Område af en romboeder
- 4.4 Areal af en romboeder
- 5 Volumen af en parallelepiped
- 5.1 Perfekt parallelepiped
- 6 Bibliografi
Elements of the Parallelepiped
Ansigter
De er hver af regionerne dannet af parallelogrammer, der begrænser parallelepiped. En parallelepiped har seks ansigter, hvor hvert ansigt har fire tilstødende ansigter og en modsat. Hvert ansigt er også parallelt med det modsatte.
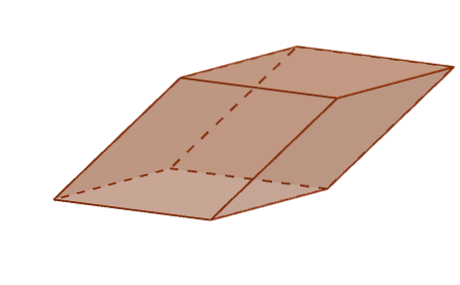
Kanter
De er den fælles side af to ansigter. I alt har en parallelepiped tolv kanter.
Hvirvel
Det er det fælles punkt med tre ansigter, der støder op til hinanden to og to. En parallelepiped har otte hjørner.

Diagonal
Givet to flader af en parallelepiped modsat hinanden, kan vi tegne et linjesegment, der går fra toppunktet på det ene ansigt til det modsatte toppunkt på det andet..
Dette segment er kendt som parallelepipediens diagonal. Hver parallelepiped har fire diagonaler.

Centrum
Det er det punkt, hvor alle diagonaler krydser hinanden.
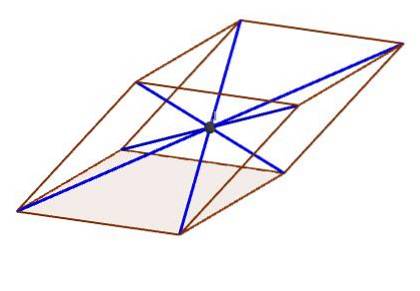
Karakteristik af Parallelepiped
Som vi allerede har nævnt, har denne geometriske krop tolv kanter, seks ansigter og otte hjørner..
I en parallelepiped kan der identificeres tre sæt dannet af fire kanter, som er parallelle med hinanden. Derudover har kanterne på disse sæt også den egenskab at have samme længde.
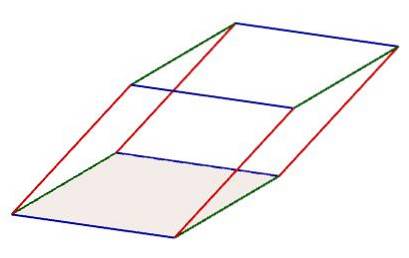
En anden egenskab, som parallelepipeder besidder, er at de er konvekse, det vil sige, hvis vi tager et par punkter, der hører til det indre af parallelepiped, vil det segment, der bestemmes af det nævnte par af punkter, også være inden i parallelepiped..
Derudover overholder parallelepipeder, der er konvekse polyedre, Eulers sætning for polyedre, hvilket giver os et forhold mellem antallet af ansigter, antallet af kanter og antallet af hjørner. Dette forhold gives i form af følgende ligning:
C + V = A + 2
Denne egenskab er kendt som Euler-karakteristikken..
Hvor C er antallet af ansigter, V antallet af hjørner og A antallet af kanter.
Typer
Vi kan klassificere parallelepipeds baseret på deres ansigter i følgende typer:
Orthohedron
De er parallelepipeds, hvor deres ansigter er dannet af seks rektangler. Hvert rektangel er vinkelret på dem, der deler en kant. De er de mest almindelige i vores daglige liv, dette er den sædvanlige form for skokasser og mursten..

Regelmæssig terning eller hexahedron
Dette er et særligt tilfælde af den foregående, hvor hvert af ansigterne er en firkant.

Terningen er også en del af de geometriske legemer kaldet platoniske faste stoffer. Et platonisk fast stof er en konveks polyhedron, så både dets ansigter og indre vinkler er lig med hinanden..
Rhombohedron
Det er en parallelepiped med romber for sit ansigt. Disse romber er alle lige til hinanden, da de deler kanter.
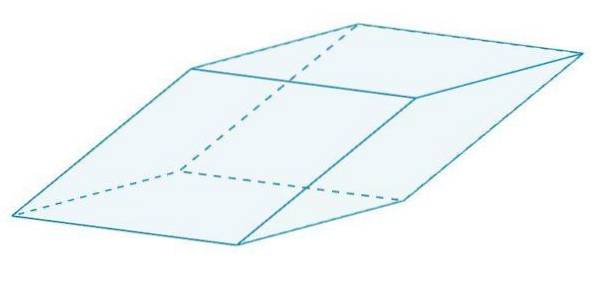
Rhombohedron
Dens seks ansigter er rhomboide. Husk at en romboide er en polygon med fire sider og fire vinkler, der er lig med to til to. Rhomboids er parallelogrammer, der hverken er kvadrater eller rektangler eller romber.

På den anden side er skrå parallelleknologiske dem, hvor mindst en højde ikke stemmer overens med deres kant. I denne klassificering kan vi inkludere rhombohedra og rhombohedra.
Diagonalberegning
For at beregne diagonalen for en orthoeder kan vi bruge Pythagoras sætning til R3.
Husk, at en ortohedron har den egenskab, at hver side er vinkelret på siderne, der deler en kant. Af denne kendsgerning kan vi udlede, at hver kant er vinkelret på dem, der deler et toppunkt.
For at beregne længden af en diagonal af en orthoeder foregår vi som følger:

1. Vi beregner diagonalen på et af ansigterne, som vi lægger som base. Til dette bruger vi den Pythagoras sætning. Lad os navngive denne diagonale db.
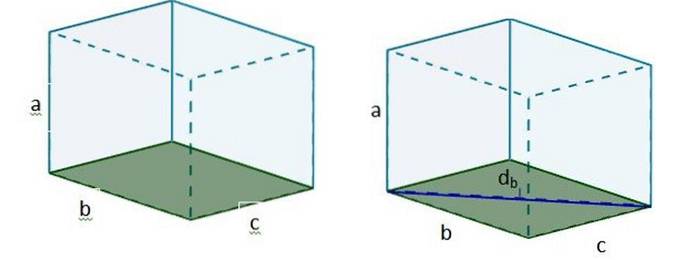
to. Derefter med db vi kan danne en ny højre trekant, således at hypotenusen i nævnte trekant er den diagonale D, der søges.
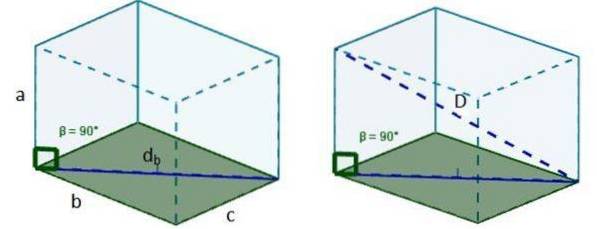
3. Vi bruger Pythagoras sætning igen, og vi har, at længden af diagonalen er:

En anden måde at beregne diagonaler på en mere grafisk måde er med summen af gratis vektorer.
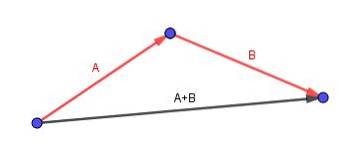
Husk at to frie vektorer A og B tilføjes ved at placere halen på vektor B med spidsen af vektor A.
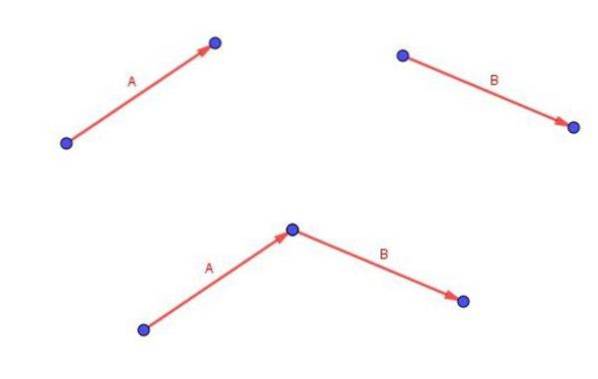
Vektoren (A + B) er den, der begynder ved halen af A og slutter ved spidsen af B.
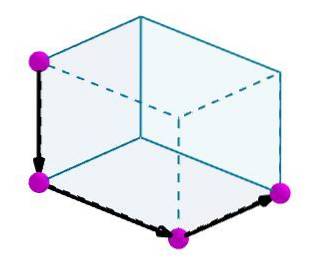
Lad os overveje en parallelepiped, som vi ønsker at beregne en diagonal for.
Vi identificerer kanterne med praktisk orienterede vektorer.
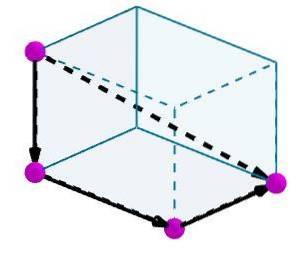
Derefter tilføjer vi disse vektorer, og den resulterende vektor vil være diagonalen af parallelepiped.
Areal
Arealet af en parallelepiped er givet af summen af hvert af områdets ansigter.
Hvis vi bestemmer en af siderne som base,
TILL + 2AB = Samlet areal
HvorhenL er lig med summen af arealerne på alle sider ved siden af basen, kaldet lateralt område og A.B er basisområdet.
Afhængigt af hvilken type parallelepiped vi arbejder med, kan vi omskrive denne formel.
Område af en ortohedron
Det er givet ved formlen
A = 2 (ab + bc + ca).
Eksempel 1
Givet følgende orthoeder, med siderne a = 6 cm, b = 8 cm og c = 10 cm, beregne arealet af parallelepiped og længden af dens diagonale.
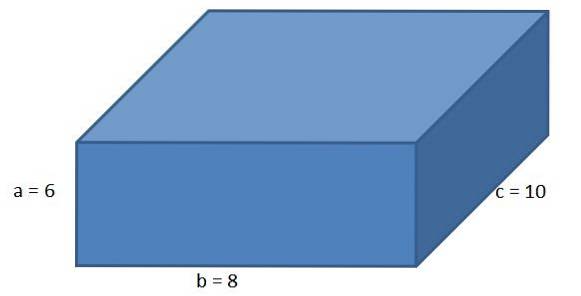
Ved at bruge formlen til området for en ortohedron har vi det
A = 2 [(6) (8) + (8) (10) + (10) (6)] = 2 [48 + 80 + 60] = 2 [188] = 376 cmto.
Bemærk, at da det er en orthoeder, er længden af en af dens fire diagonaler den samme.
Brug af Pythagoras sætning til plads har vi det
D = (6to + 8to + 10to)1/2 = (36 + 64 + 100)1/2 = (200)1/2
Område af en terning
Da hver kant har samme længde, har vi, at a = b og a = c. Udskiftning i den tidligere formel, vi har
A = 2 (aa + aa + aa) = 2 (3ato) = 6ato
A = 6ato
Eksempel 2
Kassen på en spilkonsol er formet som en terning. Hvis vi ønsker at pakke denne kasse med indpakningspapir, hvor meget papir vil vi bruge ved at vide, at længden af terningens kanter er 45 cm?
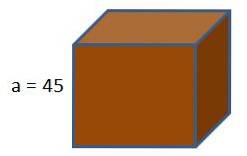
Ved hjælp af formlen for terningens område får vi det
A = 6 (45 cm)to = 6 (2025 cmto) = 12150 cmto
Område af en romboeder
Da alle deres ansigter er ens, er det nok at beregne arealet af en af dem og gang det med seks.
Vi har, at arealet af en rombe kan beregnes gennem dens diagonaler med følgende formel
TILR = (Dd) / 2
Ved hjælp af denne formel følger det, at det samlede areal af romboeder er
TILT = 6 (Dd) / 2 = 3Dd.
Eksempel 3
Ansigterne på følgende romboeder er dannet af en rombe, hvis diagonaler er D = 7 cm og d = 4 cm. Dit område vil være

A = 3 (7 cm) (4 cm) = 84 cmto.
Område af en romboeder
For at beregne arealet af en romboeder skal vi beregne arealet af romboiderne, der komponerer det. Da parallelepipeds opfylder den egenskab, at modsatte sider har samme område, kan vi knytte siderne i tre par.
På denne måde har vi, at dit område vil være
TILT = 2b1h1 + 2btohto + 2b3h3
Hvor bjeg er baserne forbundet med siderne og hjeg dens relative højde svarende til baserne.
Eksempel 4
Overvej følgende parallelepiped,

hvor side A og side A '(dens modsatte side) har en base b = 10 og en højde h = 6. Det markerede område har en værdi på
TIL1 = 2 (10) (6) = 120
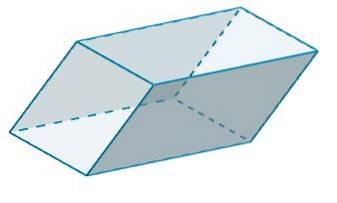
B og B 'har b = 4 og h = 6, så
TILto = 2 (4) (6) = 48

Og C og C 'har således b = 10 og h = 5, således
TIL3 = 2 (10) (5) = 100

Endelig er området for romboeder
A = 120 + 48 + 100 = 268.
Volumen af en parallelepiped
Formlen, der giver os volumenet af en parallelepiped, er produktet af arealet af en af dens ansigter i højden svarende til nævnte ansigt.
V = AChC
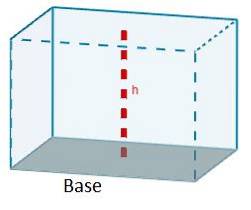
Afhængigt af typen af parallelepiped kan denne formel forenkles.
Således har vi for eksempel, at volumenet af en orthoeder vil blive givet af
V = abc.
Hvor a, b og c repræsenterer længden af ortohedronens kanter.
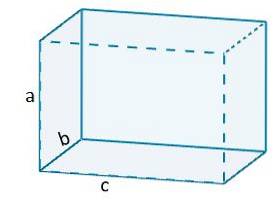
Og i det særlige tilfælde af terningen er
V = a3
Eksempel 1
Der er tre forskellige modeller til cookiebokse, og du vil vide, i hvilken af disse modeller du kan gemme flere cookies, det vil sige hvilken af kasserne der har den største volumen.
Den første er en terning, hvis kant har en længde på a = 10 cm

Dens volumen er V = 1000 cm3
Den anden har kanter b = 17 cm, c = 5 cm, d = 9 cm

Og derfor er dens volumen V = 765 cm3
Og den tredje har e = 9 cm, f = 9 cm og g = 13 cm

Og dens volumen er V = 1053 cm3
Derfor er kassen med den største lydstyrke den tredje.
En anden metode til at opnå volumenet af en parallelepiped er at bruge vektoralgebra. Især triple dot-produktet.
En af de geometriske fortolkninger, som det tredobbelte skalære produkt har, er volumenet af parallelepiped, hvis kanter er tre vektorer, der deler det samme toppunkt som udgangspunkt.
På denne måde, hvis vi har en parallelepiped, og vi vil vide, hvad dens volumen er, er det nok at repræsentere det i et koordinatsystem i R3 hvilket gør en af dens hjørner sammenfaldende med oprindelsen.

Derefter repræsenterer vi de kanter, der falder sammen ved oprindelsen med vektorer som vist i figuren.

Og på denne måde har vi, at volumenet af den nævnte parallelepiped er givet af
V = | AxB ∙ C |
Eller ækvivalent er lydstyrken determinanten for 3 × 3-matrixen, dannet af komponenterne i kantvektorerne.
Eksempel 2
Når det repræsenterer følgende parallelepiped i R3 vi kan se, at vektorerne, der bestemmer det, er følgende

u = (-1, -3,0), v = (5, 0, 0) og w = (-0,25, -4, 4)
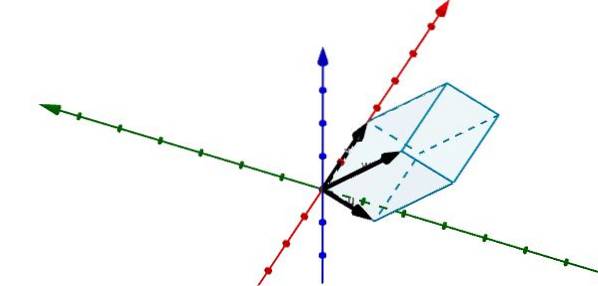
Brug af det tredobbelte produkt, vi har
V = | (uxv) ∙ w |
uxv = (-1, -3,0) x (5, 0, 0) = (0,0, - 15)
(uxv) ∙ w = (0,0, - 15) ∙ (-0,25, -4, 4) = 0 + 0 + 4 (- 15) = - 60
Ud fra dette konkluderer vi, at V = 60
Lad os nu overveje følgende parallelepiped i R3, hvis kanter bestemmes af vektorerne

A = (2, 5, 0), B = (6, 1, 0) og C = (3, 4, 4)
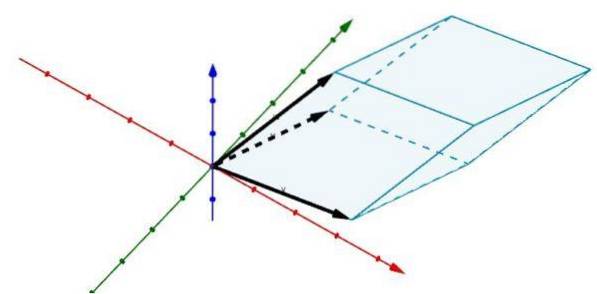
Brug af determinanter giver os det

Således har vi, at volumenet af den parallelepiped er 112.
Begge er ækvivalente måder at beregne volumen på.
Perfekt parallelepiped
En orthoeder er kendt som en Euler-mursten (eller Eulers blok), der opfylder egenskaben, at både længden af dens kanter og længden af diagonalerne på hver af dens ansigter er heltal.
Selvom Euler ikke var den første videnskabsmand, der undersøgte ortohedraet, der opfylder denne egenskab, fandt han interessante resultater om dem..
Den mindste Euler-mursten blev opdaget af Paul Halcke og længderne på dens kanter er a = 44, b = 117 og c = 240.
Et åbent problem i talteorien er som følger
Er der perfekte orthohedra?
På nuværende tidspunkt er dette spørgsmål ikke blevet besvaret, da det ikke har været muligt at bevise, at sådanne kroppe ikke eksisterer, men der er heller ikke fundet nogen..
Det, der hidtil er blevet vist, er, at der findes perfekte parallelepipeds. Den første, der bliver opdaget, har længden af dets kanter, værdierne 103, 106 og 271.
Bibliografi
- Guy, R. (1981). Uløste problemer i talteori. Springer.
- Landaverde, F. d. (1997). Geometri. Fremskridt.
- Leithold, L. (1992). Beregningen med analytisk geometri. HARLA, S.A.
- Rendon, A. (2004). Teknisk tegning: Aktivitetsbog 3 2. Baccalaureat . Tebar.
- Resnick, R., Halliday, D., & Krane, K. (2001). Fysik bind 1. Mexico: Kontinentalt.


Endnu ingen kommentarer