
Vægt (fysik) beregning, enheder, eksempler, øvelser

Det vægt det er den kraft, hvormed Jorden tiltrækker genstande til overfladen. Hver gang et objekt tabes, falder det til jorden, det er ikke i stand til at klatre alene, og det er heller ikke vægtløst midtvejs, hvilket er fordi Jorden tiltrækker det..
Alle objekter tiltrækker altid hinanden, selv de mindste, kun størrelsen af den kraft, som de gør det med, er proportional med massen. Dette betyder, at genstande med lille masse udøver lille kraft på andre, men himmellegemer som Jorden er i stand til at udøve en meget stor kraft..
Jorden holder månen i kredsløb omkring den takket være denne attraktive kraft, som kaldes tyngdekraftsattraktion når det kommer til genstande, der er langt fra jordens overflade, og vægt når genstande er tæt på.
Af dette følger, at tyngdekraften ikke kræver, at genstande nødvendigvis er i kontakt med hinanden for at kunne handle: det siges, at det siges at være en handlingskraft på afstand.
Objekter har fortsat vægt, selvom de er i en bestemt højde over jorden, og jo mere massiv de er, jo større vil denne vægt være.
Den store engelske videnskabsmand Isaac Newton var den første til at forklare dette spørgsmål gennem den universelle lov om tyngdekraft, der bærer hans navn, og som siden da har tjent til at forstå, hvordan objekter med masse interagerer. Dette er meget vigtigt, da ethvert objekt på planeten har vægt.
Artikelindeks
- 1 vægtenheder
- 1.1 Kilokraften
- 1.2 Pund-kraften
- 2 Vægtberegning og formel
- 3 Vægt som vektor
- 4 Forskelle mellem vægt, masse og volumen
- 5 Vægteksempler
- 6 Øvelse løst
- 7 Referencer
Vægtenheder
Det Internationale System af SI-enheder har som en enhed til vægtning af Newton, opkaldt efter Isaac Newton. Dette er enheden til at måle kræfter af alle slags.
Newton, forkortet N, er defineret som den nødvendige kraft for et objekt med en masse på 1 kg for at opnå en acceleration på 1 m / sto. Udover newtonen er der andre kraftenheder, der er i almindelig brug, for eksempel følgende:
Kilokraften
Det kilo-kraft eller kilopond, forkortet kg-f eller kp, selvom det almindeligvis kaldes kg uden mere, er den kraft, som Jorden udøver på et objekt, der er ved havoverfladen og 45 ° nordlig bredde. Det er nødvendigt at specificere placeringen, da gravitationsfeltet som sagt oplever variationer med højde og bredde.
Når nogen siger, at han vejer 45 kg, hvad han virkelig mener er, at hans vægt er 45 kg-f, fordi kilogrammet er den enhed, der er forbeholdt masse.
Ækvivalensen mellem kg-f og N er: 1 kg-f = 9,8 N
Pund-kraft
Det pund-kraft, forkortet lb-f er også en kraftenhed, der er analog med kg-f, da det er den kraft, som Jorden udøver på et objekt på 1 lb masse. Og som med kg-f er der ikke noget problem med værdierne, når du er på Jorden, det vil sige et objekt med masse l lb, vejer 1 lb-f.
Ækvivalensen i lb-f og N er: 1 lb-f ≡ 4.448222 N.
Vægtberegning og formel
Vægten af et objekt er proportional med dets masse. Jo større masse, jo større vægt.
Formlen til at finde størrelsen af vægten P (eller også W, som det undertiden betegnes, med "Vægt" på engelsk) er meget enkel:
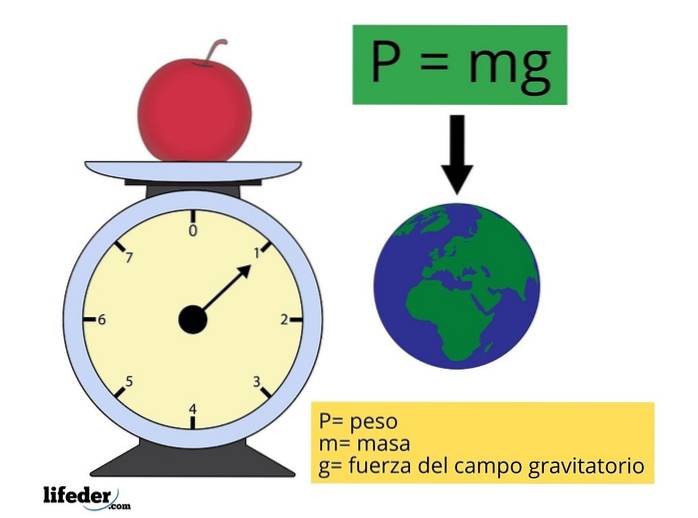
P = mg
Hvor m repræsenterer genstandens masse og g er størrelsen af tyngdeacceleration (tyngdefeltets eller tyngdekraftens intensitet), omtrent konstant, og hvis værdi tages som 9,81 m / sto for de hyppigste beregninger.
Vægt er en vektor, og fede bogstaver bruges til at skelne mellem en vektor og dens størrelse. Når man taler om P, forstås på denne måde, at det er den numeriske værdi, og når den er skrevet P der henvises til vektoren:
P = m ∙g
Det g med fed skrift er Jordens tyngdefelt, det vil sige den indflydelse, som Jorden udøver på det rum, der omgiver den, uanset om der er en anden krop, der opfatter det eller ej. Ethvert objekt med masse har sit eget tyngdefelt, det være sig lille eller stor.
Intensiteten af Jordens tyngdefelt g det er ikke helt konstant. Det har små variationer, der hovedsageligt opstår, fordi Jorden ikke er en perfekt sfære og også på grund af lokale forskelle i højde og tæthed. Men for de fleste applikationer er værdien 9,81 m / sto Det fungerer meget godt.
Andre himmellegemer har deres eget karakteristiske tyngdefelt, hvorfor tyngdeaccelerationen varierer afhængigt af planeten eller satellitten. Det samme objekt ville have en forskellig vægt i hver enkelt, derfor er vægt ikke en karakteristisk egenskab for ting, men af materie generelt..
Vægt som vektor
Vægt er en vektor og har derfor størrelse, retning og sans. I nærheden af jordoverfladen er vægten en vektor i lodret retning, og retningen er altid nede.
Normalt er den lodrette retning navngivet som aksen Y eller z, og den nedadgående retning tildeles et + eller - tegn for at skelne det fra den opadgående retning. Valget afhænger af placeringen af oprindelsen. På billedet nedenfor blev oprindelsen valgt på det sted, hvorfra æblet falder:
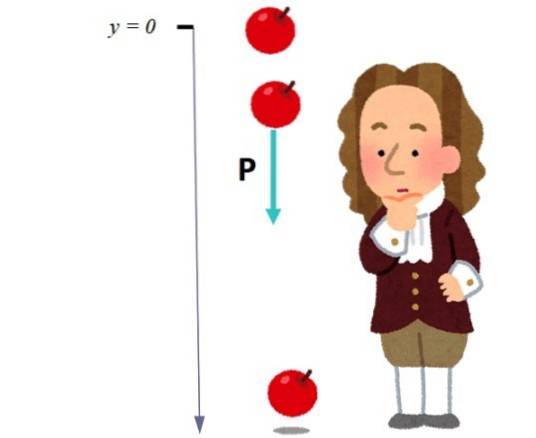
Enhedsvektoren j, en vektor med størrelsesorden lig med 1 bruges til at markere og skelne den lodrette retning. Med hensyn til denne vektor er vægten skrevet således:
P = mg (- j)
Hvor negativt tegn er tildelt nedadgående retning.
Forskelle mellem vægt, masse og volumen

Disse tre begreber forveksles ofte, men når man gennemgår vægtens egenskaber, er det let at skelne det fra masse og volumen..
Til at begynde med afhænger vægten af tyngdefeltet, hvor objektet er. For eksempel har den samme ting på jorden og på månen en anden vægt, selvom antallet af atomer, der komponerer den, forbliver konstant..
Masse er en skalar størrelse, der er relateret til antallet af atomer, der udgør objektet, og det fremgår af den modstand, som objektet har til at ændre sin bevægelse, en egenskab kaldet inerti.
For sin del er volumen målet for det rum, som et objekt optager, en anden skalar mængde. To genstande med samme volumen vejer ikke det samme, for eksempel vejer en jernterning meget mere end en polystyrenterning med de samme dimensioner.
Sammenfattende:
- Masse er relateret til mængden af stof, som et legeme har.
- Vægt er den kraft, som jorden udøver på denne masse, proportional med den.
- Volumen er det rum, der er optaget af stof.
Det skal bemærkes, at hverken masse eller volumen er retning eller sans, men kun numerisk værdi og en passende enhed, hvis de er skalære størrelser. På den anden side skal vægten, som en vektor, altid udtrykkes korrekt med angivelse af størrelsen, enheden, retningen og følelsen, som i det foregående afsnit.
Vægteksempler
Alle objekter på jorden har vægt, du kan endda "veje" objekter, der ikke er på jorden, såsom andre planeter eller solen, selvom det naturligvis ved indirekte hjælp.
Da rækkevægten er meget stor, anvendes videnskabelig notation (med en styrke på 10) til at udtrykke nogle, der er meget store eller meget små:
-Solen: 1.989 × 1030 kg-f
-Jupiter: 1.898 × 1027 kg-f
-En myg: 2,0 × 10-5 N
-Babyer: 34,3 N
-Et barn: 353 N.
-Voksen person: 65 kg-f
-En voksen elefant: 5,5 × 103 kg-f
-Blåhval: 1,0 × 106 N
Træning løst
En kasse med en vægt på 20 kg hviler på et bord.
a) Find vægten af kassen og den normale kraft, som tabellen udøver på den.
b) En anden 10 kg kasse placeres oven på den første. Find det normale, som bordet udøver på 20 kg kassen, og det normale, som dette udøver på den mindre kasse.
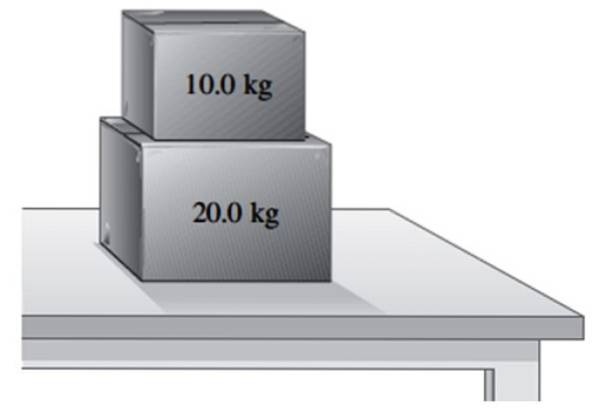
Løsning til
Det er praktisk at lave et frit kropsdiagram på kassen, som består af at tegne de kræfter, der virker på den.
I denne situation er den mindste kasse endnu ikke på toppen, derfor er der kun to kræfter: den første er vægt. P som er trukket lodret nedad som angivet i de foregående sektioner, og så er der det normale N, som er den lodrette kraft, som bordet udøver, og forhindrer kassen i at falde.
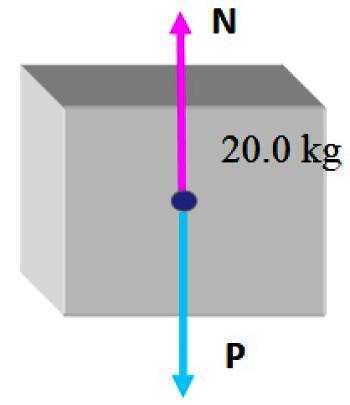
Da kassen er i statisk ligevægt under disse omstændigheder, er det rimeligt at konkludere, at størrelsen af det normale er det samme som vægten, så det kan kompensere, derfor:
N = mg = 20,0 kg x 9,8 m / sto = 196 N; rettet lodret op.
Vægten er på sin side P = 196 N rettet lodret nedad.
Løsning b
Nu laves der nye fritlegemsdiagrammer på begge objekter. For den store kasse ændres tingene lidt, da den lille kasse udøver kraft på den.
Styrkerne er som følger: N Y P er henholdsvis det normale, der udøves af tabellen, og vægten på kassen på 20,0 kg, der ikke ændrede sig. Og den nye kraft, der udøves af den lille kasse er N1, normal på grund af kontakt med den store bokses overside.
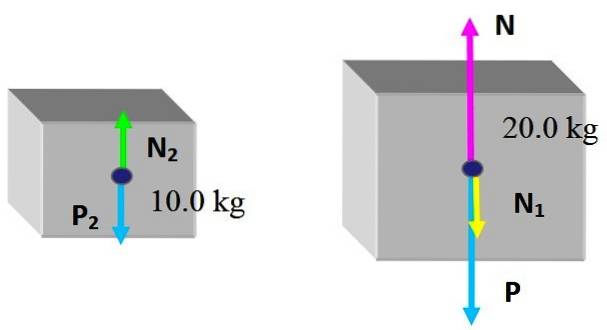
Hvad angår den lille kasse, modtager den det normale Nto, udøvet af den store bokses overside og selvfølgelig dens vægt Pto. Da kasserne er i statisk ligevægt:
Nto - Pto = 0
N - N1 - P = 0
Fra den første ligning har vi den Nto = Pto = 10 kg x 9,8 m / sto = 98 N. Ifølge handlingsloven og reaktionen er størrelsen af den kraft, som den lille kasse modtager, den samme som den udøver på den store kasse, så:
Nto = N1 = 98 N
Fra den anden ligning ryddes den normale N, der udøves af tabellen på den store kasse, som igen har den lille kasse ovenpå:
N = N1 + P = 98 N + 196 N = 294 N
Referencer
- Figueroa, D. 2005. Serie: Physics for Sciences and Engineering. Bind 2. dynamik. Redigeret af Douglas Figueroa (USB).
- Giambattista, A. 2010. Fysik. 2. plads Ed. McGraw Hill.
- Giancoli, D. 2006. Fysik: Principper med applikationer. 6. Ed prentice hall.
- Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14. Red. Bind 1. Pearson.
- Serway, R., Jewett, J. 2008. Fysik til videnskab og teknik. Bind 1. 7. Ed. Cengage Learning.
- Thomas Griffith, W. 2007. Konceptuel fysik. Mc Graw Hill.



Endnu ingen kommentarer