
Elektrisk potentialeformel og ligninger, beregning, eksempler, øvelser
Det elektrisk potentiale det defineres til enhver tid, hvor der findes et elektrisk felt, som den potentielle energi for dette felt pr. enhedsopladning. Punktladninger og punkt- eller kontinuerlige ladningsfordelinger frembringer et elektrisk felt og har derfor et tilhørende potentiale.
I det internationale system for enheder (SI) måles det elektriske potentiale i volt (V) og betegnes som V. Matematisk udtrykkes det som:
V = U / qeller

Hvor U er den potentielle energi forbundet med ladning eller distribution og qeller det er en positiv testladning. Da U er en skalar, er potentialet det også.
Fra definitionen er 1 volt simpelthen 1 Joule / Coulomb (J / C), hvor Joule er SI-enheden for energi, og Coulomb (C) er enheden til elektrisk ladning..
Antag en punktafgift q. Vi kan kontrollere arten af det felt, som denne ladning producerer ved hjælp af en lille, positiv testladning, kaldet qeller, brugt som sonde.
Arbejdet W havde brug for at flytte denne lille belastning fra punktet til indtil punktet b, er det negative af forskellen på potentiel energi ΔU mellem disse punkter:
Wa → b = -ΔU = - (Ub - ELLERtil)
Opdeler alt mellem qeller:
Wa → b / qeller= - ΔU / qeller = - (Ub - ELLERtil) / qeller = - (V.b - Vtil) = -AV
Her Vb er potentialet ved punkt b og Vtil er det i punkt a. Den potentielle forskel Vtil - Vb er potentialet i omkring b og kaldes Vab. Rækkefølgen af abonnementerne er vigtig, hvis den blev ændret, ville den repræsentere potentialet for b med hensyn til a.
Artikelindeks
- 1 Elektrisk potentialforskel
- 1.1 Tegn og værdier for den potentielle forskel
- 2 Sådan beregnes det elektriske potentiale?
- 2.1 Elektrisk potentiale for diskrete ladningsfordelinger
- 2.2 Elektrisk potentiale ved kontinuerlig belastningsfordeling
- 3 Eksempler på elektrisk potentiale
- 3.1 Batterier og batterier
- 3.2 Stikkontakt
- 3.3 Spænding mellem ladede skyer og jorden
- 3.4 Van Der Graff generator
- 3.5 Elektrokardiogram og elektroencefalogram
- 4 Øvelse løst
- 4.1 Løsning a
- 4.2 Løsning b
- 4.3 Løsning c
- 4.4 Løsning d
- 4.5 Løsning e
- 4.6 Løsning f
- 5 Referencer
Elektrisk potentialforskel
Af det foregående følger, at:
-AV = Wa → b / qeller
Derfor:
AV = -Wa → b / qeller
Nu beregnes arbejdet som integralet af det skalære produkt mellem den elektriske kraft F mellem q og qeller og forskydningsvektoren dℓ mellem punkt a og b. Da det elektriske felt er kraft pr. Enhedsenhed:
OG = F/ qeller
Arbejdet med at bære testbelastningen fra a til b er:
Denne ligning giver mulighed for direkte at beregne potentialforskellen, hvis ladningens elektriske felt eller den distribution, der producerer det, tidligere er kendt..
Og det bemærkes også, at den potentielle forskel er en skalar størrelse, i modsætning til det elektriske felt, som er en vektor.
Tegn og værdier for den potentielle forskel
Fra den tidligere definition observerer vi, at hvis OG og dℓ er vinkelrette, er potentialforskellen AV nul. Dette betyder ikke, at potentialet på sådanne punkter er nul, men at det blot er Vtil = Vb, potentialet er konstant.
Linjerne og overfladerne, hvor dette sker, kaldes potentiale. F.eks. Er de ækvipotentiale linjer i feltet for en punktladning omkredse koncentriske til ladningen. Og de ækvipotentiale overflader er koncentriske kugler.
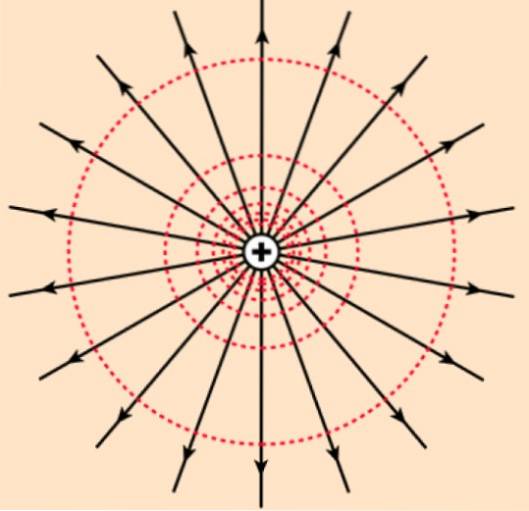
Hvis potentialet produceres af en positiv ladning, hvis elektriske felt består af radiale linjer, der projicerer ladningen, når vi bevæger os væk fra marken, bliver potentialet mindre og mindre. Som testbelastning qeller er positiv, føler du mindre elektrostatisk frastødning jo længere du er fra q.

Tværtimod, hvis belastningen hvad er negativ, testopladningen qeller (positivt) vil have et lavere potentiale, når det kommer tættere på hvad.
Sådan beregnes det elektriske potentiale?
Ovenstående integral tjener til at finde potentialforskellen og derfor potentialet på et givet punkt b, hvis referencepotentialet er kendt på et andet tidspunkt til.
For eksempel er der tilfældet med en punktbelastning hvad, hvis elektriske feltvektor på et punkt placeret på afstand r af lasten er:
OG = kq / rto r
Hvor k er den elektrostatiske konstant, hvis værdi i internationale systemenheder er:
k = 9 x 10 9 Nmto / Cto.
Og vektoren r er enhedsvektoren langs linien, der forbinder hvad med punkt P.
Det erstattes i definitionen af AV:

At vælge det punkt b være på afstand r af ladningen, og at når a → ∞ potentialet er 0, så er Vtil = 0 og den foregående ligning er som:
V = kq / r
Vælg Vtil = 0 når a → ∞ giver mening, for på et punkt meget langt fra belastningen er det vanskeligt at opfatte, at den eksisterer.
Elektrisk potentiale for diskrete ladningsfordelinger
Når der er mange punktladninger fordelt i en region, beregnes det elektriske potentiale, som de producerer på ethvert punkt P i rummet, og tilføjer de individuelle potentialer, som hver enkelt producerer. A) Ja:
V = V1 + Vto + V3 +… VN = ∑ Vjeg
Summationen strækker sig fra i = til N, og potentialet for hver ladning beregnes ved hjælp af ligningen givet i det foregående afsnit.
Elektrisk potentiale ved kontinuerlige belastningsfordelinger
Med udgangspunkt i potentialet for en punktladning kan vi finde potentialet produceret af et ladet objekt med en målelig størrelse på ethvert punkt P.
For at gøre dette er kroppen opdelt i mange små uendelige ladninger dq. Hver bidrager til det fulde potentiale med en dV uendelig.

Derefter tilføjes alle disse bidrag gennem en integral, og således opnås det samlede potentiale:

Eksempler på elektrisk potentiale
Der er elektrisk potentiale i forskellige enheder, takket være det er det muligt at få elektrisk energi, f.eks. Batterier, bilbatterier og stikkontakter. Elektriske potentialer er også etableret i naturen under elektriske storme.
Batterier og batterier
I celler og batterier lagres elektrisk energi gennem kemiske reaktioner inde i dem. Disse opstår, når kredsløbet er lukket, hvilket giver jævnstrøm til at strømme og en pære til lys, eller bilens startmotor kører..
Der er forskellige spændinger: 1,5 V, 3 V, 9 V og 12 V er de mest almindelige.
Outlet
Hvidevarer og apparater, der kører på kommerciel vekselstrøm, er forbundet til en forsænket stikkontakt. Afhængigt af placeringen kan spændingen være 120 V eller 240 V.

Spænding mellem ladede skyer og jorden
Det er den der opstår under storme på grund af bevægelse af elektrisk ladning gennem atmosfæren. Det kan være i størrelsesordenen 108 V.

Van Der Graff generator
Takket være et gummibånd frembringes friktionsladning, der akkumuleres på en ledende kugle placeret oven på en isolerende cylinder. Dette genererer en potentiel forskel, der kan være flere millioner volt.

Elektrokardiogram og elektroencefalogram
I hjertet er der specialiserede celler, der polariserer og depolariserer, hvilket forårsager potentielle forskelle. Disse kan måles som en funktion af tiden ved hjælp af et elektrokardiogram..
Denne enkle test udføres ved at placere elektroder på personens bryst, der er i stand til at måle små signaler..
Da de er meget lave spændinger, skal du forstærke dem bekvemt og derefter optage dem på et papirbånd eller se dem gennem computeren. Lægen analyserer impulser for abnormiteter og registrerer således hjerteproblemer.

Hjernens elektriske aktivitet kan også registreres med en lignende procedure, kaldet EEG..
Træning løst
En belastning Spørgsmål = - 50,0 nC er placeret 0,30 m fra punktet TIL og 0,50 m fra punkt B, som vist i den følgende figur. Svar på følgende spørgsmål:
a) Hvad er potentialet i A produceret af denne afgift?
b) Og hvad er potentialet i B?
c) Hvis en ladning q bevæger sig fra A til B, hvad er den potentielle forskel, gennem hvilken den bevæger sig?
d) Stiger eller falder potentialet ifølge det foregående svar??
e) Hvis q = - 1,0 nC, hvad er ændringen i dens elektrostatiske potentielle energi, når den bevæger sig fra A til B?
f) Hvor meget arbejde udfører det elektriske felt produceret af Q, når testladningen bevæger sig fra A til B?

Løsning til
Q er en punktladning, derfor beregnes dens elektriske potentiale i A ved:
VTIL = kQ / rTIL = 9 x 109 x (-50 x 10-9) / 0,3 V = -1500 V
Løsning b
På samme måde
VB = kQ / rB = 9 x 109 x (-50 x 10-9) / 0,5 V = -900 V
Løsning c
AV = Vb - Vtil = -900 - (-1500) V = + 600 V.
Løsning d
Hvis ladningen q er positiv, øges dens potentiale, men hvis den er negativ, falder dens potentiale.
Løsning e
ΔV = UU / qeller → ΔU = qeller AV = -1,0 x 10-9 x 600 J = -6,0 x 10-7 J.
Det negative log ind ΔU angiver, at den potentielle energi i B er mindre end A.
Løsning f
Da W = -ΔU realiseres feltet +6,0 x 10-7 J af arbejde.
Referencer
- Figueroa, D. (2005). Serie: Fysik til videnskab og teknik. Volumen 5. Elektrostatik. Redigeret af Douglas Figueroa (USB).
- Giambattista, A. 2010. Fysik. 2. plads Ed. McGraw Hill.
- Resnick, R. (1999). Fysisk. Bind 2. 3. udgave på spansk. Compañía Editorial Continental S.A. af C.V.
- Tipler, P. (2006) Fysik til videnskab og teknologi. 5. udg. Bind 2. Editorial Reverté.
- Serway, R. Fysik til videnskab og teknik. Bind 2. 7. Ed. Cengage Learning.



Endnu ingen kommentarer