
Hydrostatisk trykformel, beregning, eksempler, øvelser

Det hydrostatisk tryk er den, der udøver en væske i statisk ligevægt på ethvert tidspunkt i dens indre, det være sig en overflade nedsænket i den, beholdervæggene eller en del af væske, der udgør en del af den samlede masse.
Den måde, hvorpå væsker udøver tryk, adskiller sig fra faste stoffer. Disse udøver tryk nedad, men en væske eller gas gør det i alle retninger.

Når det kommer til en væske, stiger trykket med dybden, som det er kendt fra erfaring, når man dykker ned i vand, hvor stigningen i tryk mærkes i ørerne. Dette tryk kommer fra væskens vægt og den uophørlige bevægelse af de partikler, der sammensætter den, som kontinuerligt rammer overfladen af kroppen nedsænket i væsken..
Hvis vi antager en ukomprimerbar væske - hvilket er sandt i langt de fleste anvendelser - forbliver dens densitet konstant, og i dette tilfælde afhænger trykket lineært af dybden..
Artikelindeks
- 1 Formel
- 2 Eksempler på hydrostatisk tryk
- 2.1 Strukturer, hvor hydrostatisk tryk er relevant
- 3 Øvelser
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 4 Referencer
Formel
Hydrostatisk tryk beregnes ved hjælp af følgende udtryk:
P = Ppengeautomat + ρ · g · h
Hvor:
-P det tryk, der udøves på et punkt
-Ppengeautomat er atmosfærens tryk ved den frie overflade
-ρ er densiteten af væsken
-g er tyngdeacceleration
-h er den dybde, hvor du vil beregne det hydrostatiske tryk
Formlen inkluderer effekterne af atmosfæren, men mange manometre eller manometre placerer 0 i det atmosfæriske tryk. Derfor måler de det differenstryk eller det relative tryk, også kaldet overtryk:
Pm = ρ · g · h
Med hensyn til gasser komprimerer eller ekspanderer de meget let. Derfor er dens densitet, som er forholdet mellem masse og volumen, normalt en funktion af andre parametre, såsom højde og temperatur, i tilfælde af atmosfæriske gasser..
Trykket fra gasser kaldes ofte aerostatisk tryk, idet udtrykket hydrostatisk tryk er forbeholdt væsker.
Eksempler på hydrostatisk tryk
Det hydrostatiske tryk afhænger kun af dybden, så formen eller arealet af beholderens bund er ikke relevant.
Da tryk P er defineret som den lodrette komponent af kraft F pr. Enhed A:
P = F / A
Derefter kan den kraft, der udøves af væsken i bunden af en beholder, være forskellig, men da den fordeles over forskellige udvidelser, er trykket, som er forholdet mellem kraft og areal, det samme for punkter i samme dybde..
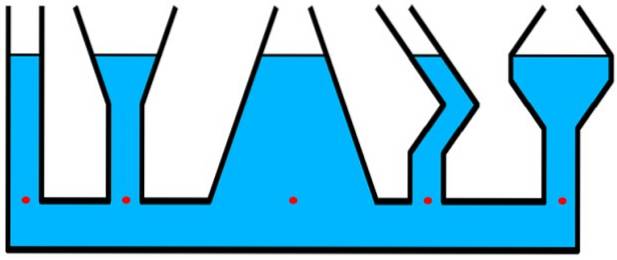
Overvej beholderne i figuren. Trykket er det samme for alle de røde prikker, der er på samme niveau, selvom der er en større mængde væske over dette niveau i den centrale beholder - bredere - end der er det cylindriske og tynde rør yderst til venstre..
Strukturer, hvor hydrostatisk tryk er relevant
-En dæmnings vægge: skønt kraften er den samme for alle punkterne på den flade bund, vokser den på den lodrette væg, når dybden øges, det er grunden til, at støttevæggene er bredere i bunden end øverst.
-På væggene og bunden af en swimmingpool.
-I stjerner som vores sol, hvor hydrostatisk tryk afbalancerer tyngdekraften og holder stjernen i gang. Når denne balance er brudt, kollapser stjernen og gennemgår ekstreme ændringer i dens struktur..
-Flydende lagertanke designet til at modstå hydrostatisk tryk Ikke kun væggene, men porte, der letter påfyldning og udvinding. For dets design tages det i betragtning, hvis væsken er ætsende, og også det tryk og den kraft, den udøver i henhold til dens densitet.
-Dæk og balloner, der oppustes på en sådan måde, at de modstår trykket fra væsken (gas eller væske) uden at rive.
-Ethvert neddykket legeme, der oplever et lodret opadgående tryk eller "lysning" af dets vægt takket være det hydrostatiske tryk, som væsken udøver. Dette er kendt som Archimedes 'princip.
Uddannelse
Archimedes 'princip siger, at når et legeme er nedsænket helt eller delvist, vil det opleve en opadgående lodret kraft, kendt som stød. Stødkraftens størrelse er numerisk lig med vægten af volumenet af vand, der forskydes af objektet..

Lad ρvæske væskens tæthed, Vs det nedsænkede volumen, g tyngdeaccelerationen og B størrelsen af tryk, som vi kan beregne ved hjælp af følgende udtryk:
B = ρvæske .Vs .g
- Øvelse 1
En rektangulær blok, hvis dimensioner er 2,0 cm x 2,0 cm x 6,0 cm flyder i ferskvand med sin længste akse lodret. Længden af blokken, der stikker ud over vandet, er 2,0 cm. Beregn densitet af blokken.
Opløsning
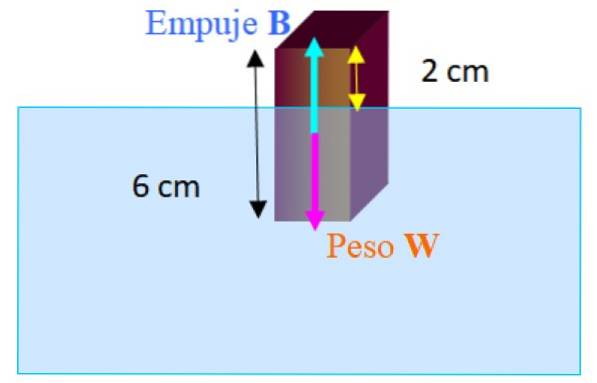
De kræfter, der virker på blokken, er vægten W ned og stød B opad. Da blokken flyder i ligevægt, har vi:
∑ FY = B - W = 0
B = W
Størrelsen af vægten W er produktet af blokens masse m og tyngdeacceleration. Vi bruger definitionen af densiteten ρeller som kvotienten mellem massen m og lydstyrken V af blokken:
ρeller = m / V → m = ρeller . V
For sin del er kraften:
B = ρvæske .Vs .g
Ligestilling af trykstørrelse og vægtstørrelse:
ρvæske .Vs .g = ρeller . F.eks
Tyngdekraften annulleres ved at være en faktor på begge sider, og blokens tæthed kan løses som:
ρeller = ρvæske . (Vs / V)
Vandtætheden i internationale systemenheder er 1000 kg / m3. Volumenene er i alt V og nedsænket Vs, beregnes ved hjælp af V = bredde x højde x dybde:
V = 2,0 cm x 2,0 cm x 6,0 cm = 24,0 cm3
Vs = 2,0 cm x 2,0 cm x 4,0 cm = 16,0 cm3
Erstatning af værdier:
ρeller = ρvæske . (Vs / V) = 1000 kg / m3 . (16/24) = 667 kg / m3
- Øvelse 2
Beregn procentdelen af nedsænket volumen af et stykke is, der flyder i havvand ved 0 ºC.
Opløsning
Is flyder på vand, da dens densitet er lavere: 916,8 Kg / m3, hvilket betyder, at det udvides, når det afkøles, i modsætning til de fleste stoffer, der øges i volumen, når det opvarmes.

Det er en meget heldig omstændighed for livet, siden da fryser vandmasserne kun på overfladen og forbliver flydende i dybden.
Tætheden af havvand er lidt højere end for ferskvand: 1027 Kg / m3. Vi beregner volumenfraktionen V.s / V:
Vs / V = ρeller / ρvæske = 916,8 kg / m3 / 1027 kg / m3 = 0,8927
Dette betyder, at ca. 89% af isen forbliver nedsænket under vand. Kun 11% er synlig flydende på havet.
Referencer
- Giambattista, A. 2010. Fysik. 2. plads Ed. McGraw Hill.
- Knight, R. 2017. Fysik for forskere og teknik: en strategi tilgang. Pearson.
- Cimbala, C. 2006. Fluid Mechanics, Fundamentals and Applications. Mc. Graw bakke.
- Hibbeler, R. 2015. Fluid Mechanics. 1. Ed. Pearson.
- Mott, R. 2006. Fluid Mechanics. 4. plads Udgave. Pearson Uddannelse.
- Streeter, V. 1999. Fluid Mechanics. Mcgraw bakke.



Endnu ingen kommentarer