
Princippet om transmission af kræfter
Hvad er princippet om overførbarhed?
Det overførselsprincippet påføres faste genstande og angiver, at en kraft, der påføres et eller andet punkt på kroppen, er ækvivalent med en anden kraft af samme størrelse og retning, så længe kraften påføres i den samme linje, der indeholder den oprindelige kraft.
Derfor vil enhver kraft af samme størrelse og retning medføre den samme virkning af translationel og rotationsbevægelse på objektet, så længe dets anvendelsespunkt er placeret på samme linje, som vist i den følgende figur.
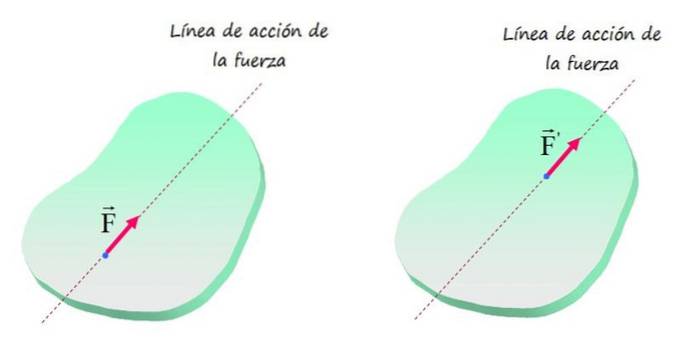
De viste kræfter F Y F'de siges at være ækvivalente kræfter og den stiplede lige linje, der indeholder dem, kaldes handlingslinje for kraft.
Princippet om overførsel er meget nyttigt, da det gør det muligt for de kræfter, der virker på objektet, at glide på bekvemmelighed for at lette analysen..
Forklaring til overførselsprincippet
Princippet om overførsel er baseret på det faktum, at to kræfter F1 Y Fto er ækvivalente, forudsat at de har samme størrelse og samme retning.
Derudover skal de producere det samme øjeblik i forhold til ethvert punkt O, hvilket er garanteret ved at have den samme handlingslinje, og fordi øjeblikket er et produkt af kraft gange afstanden fra O til linjen..
Bemærk, at princippet kun gælder for et stift legeme, det vil sige et objekt, hvori den relative afstand mellem dets dele ikke ændres, fordi de interne kræfter, der holder det sammen, er stærke nok. Derfor ændrer objektet ikke sin form, uanset om eksterne kræfter virker på det eller ej..
På den anden side, hvis genstanden ikke er stiv, ville en ændring af anvendelsespunktet for kræfterne medføre variationer med hensyn til den spænding eller kompression, der påføres kroppen, hvilket ville føre til ændringer i dens form..
At antage, at et legeme er stift, er naturligvis intet mere end en idealisering, da i virkeligheden alle genstande er deformerbare i større eller mindre grad. I mange tilfælde er dette imidlertid en glimrende tilnærmelse, hvis deformationen er lille nok til at blive betragtet som ubetydelig..
Begrænsninger
Transmissibilitetsprincippet har som angivet en begrænsning med hensyn til de interne virkninger af rullende eller glidende kræfter. Den følgende figur viser et objekt med kræfterne F Y F'anvendt på forskellige punkter i samme handlingslinje.
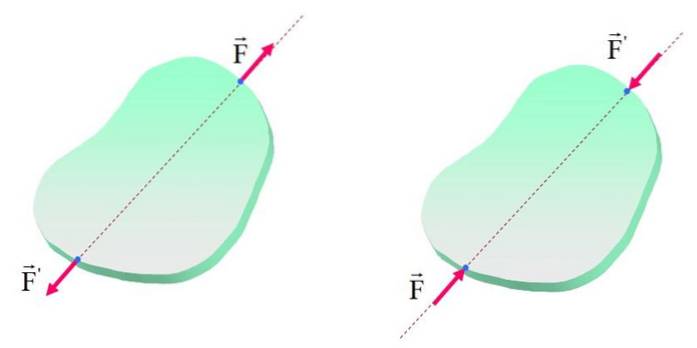
Bemærk at i begge figurer er kroppen (stiv eller ej) i ligevægt, da kræfterne har samme størrelse og retning og modsatte retninger. Desuden er kræfterne, som sagt, på samme handlingslinje, men i venstre figur er effekten på kroppen af spænding, mens den i højre side er kompression..
Derfor, selvom kroppen forbliver i ro, er de indre effekter forskellige og bliver tydelige, hvis objektet ikke er helt stift. For venstre er kræfterne tilbøjelige til at forlænge kroppen, mens de i højre side har en tendens til at forkorte det.
Eksempler på overførselsprincippet
Eksempel 1
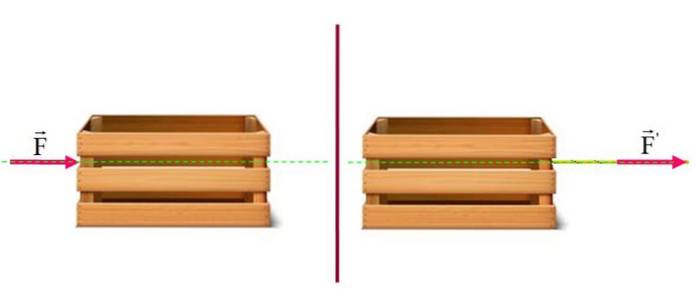
Antag at du har et tungt bagagerum på et vandret gulv. Effekten af at blive skubbet fra venstre side er den samme som at blive trukket af et vandret reb fra højre side, mens begge kræfter påføres langs den viste grønne vandrette linje. I dette tilfælde er bagagerumets bevægelse den samme.
Eksempel 2
Der er en lang planke som en hylde. For at installere det svarer det til at fastgøre det fra loftet ved hjælp af reb i enderne end at placere stivere under, også i samme ender.
I begge tilfælde vil de kræfter, der afbalancerer planken, have samme størrelse og retning, der virker på de samme handlingslinjer, men anvendes på forskellige punkter..
Princippet om overførelighed og øjeblikke
Antag, at vi har en kraft F anvendt ved et punkt A, det øjeblik, der stammer fra denne kraft omkring det punkt O, der er vist i figuren, er:
MELLER = rTIL × F
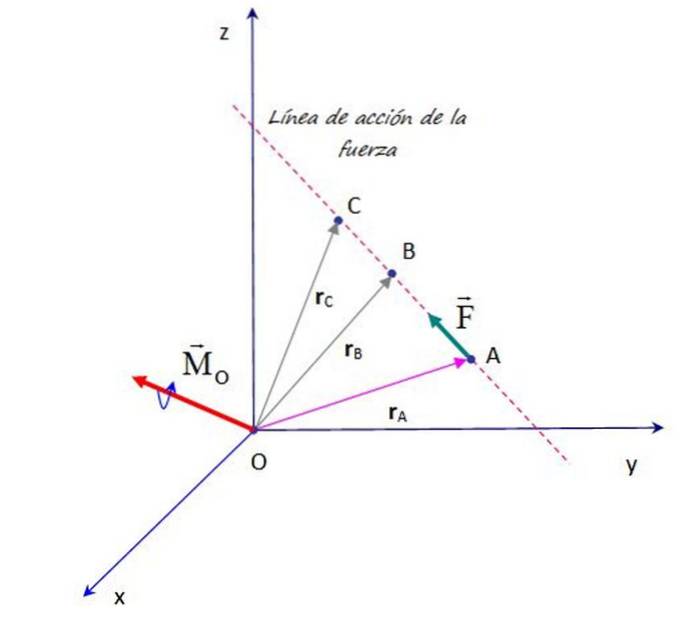
Princippet om overførelighed sikrer det F, handler på et hvilket som helst punkt langs dets handlingslinje, for eksempel punkterne B, C og mere, har det samme øjeblik med hensyn til punkt O. Derfor er det gyldigt at bekræfte, at:
MELLER = rTIL × F = rB × F = rC × F
Løst øvelser
Øvelse 1
En homogen kugle har masse M = 5 kg og understøttes i hvile på en vandret overflade uden friktion.
-
- a) Tegn i et diagram den kraft, som overfladen udøver på kuglen.
- b) Konstruer kuglens frie kropsdiagram
- c) Beregn værdien af den normale kraft, som overfladen udøver på kuglen.
-
Løsninger a og b
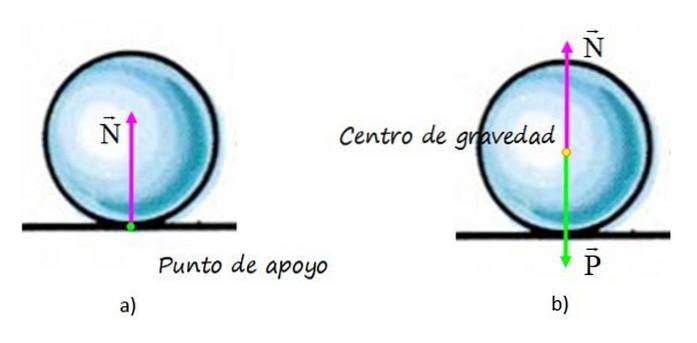
Graf a) viser den kraft, der udøves af overfladen på kuglen, kaldet normal N, da det er vinkelret på overfladen. Anvendelsespunktet for kraften falder sammen med kuglens støttepunkt på overfladen (punkt i grøn farve), og handlingslinjen er den lodrette, der passerer gennem kuglens geometriske centrum..
I graf b) er kuglens frie kropsdiagram, hvor bortset fra det normale vises vægten, som påføres i tyngdepunktet, betegnet med punktet i gult.
Takket være overførselsprincippet, den normale kraft N det kan flyttes op til dette punkt uden at ændre dets virkninger på sfæren. Disse effekter er ingen ringere end at holde kuglen hvilende på bordet i balance..
-
Løsning c
Da kuglen er i ligevægt og tager lodret opad som positiv og negativ lodret nedad, resulterer Newtons anden lov i:
N - P = 0
Det vil sige vægten og den normale balance, derfor er de lige store:
N = P = Mg = 5 kg × 9,8 m / sto = 49 N, lodret lodret opad.
Øvelse 2
Angiv, om overførselsprincippet er opfyldt i følgende tilfælde:
-
Første sag
En 20 N-kraft, der påføres vandret på et stift legeme, erstattes af en anden 15 N-kraft, der påføres et andet sted på kroppen, skønt begge påføres i samme retning.
-
- Opløsning
I dette tilfælde vil princippet om overførbarhed ikke blive opfyldt, da skønt de to kræfter påføres i samme retning, har den anden kraft ikke den samme størrelse som den første. Derfor findes der ikke en af de uundværlige betingelser for overførselsprincippet..
-
Anden sag
En 20 N kraft påført vandret på en stiv krop erstattes af en anden 20 N kraft, påført på et andet punkt på kroppen og lodret.
-
- Opløsning
Ved denne lejlighed er princippet om overførbarhed ikke opfyldt, da selvom de to kræfter har samme modul, anvendes de ikke i samme retning. Igen findes en af de uundværlige betingelser for overførselsprincippet ikke. Det kan siges, at de to kræfter er ækvivalente.
-
Tredje sag
En kraft på 10 N, der påføres vandret på et stift legeme, udveksles til et andet også på 10 N, der påføres et andet sted på kroppen, men i samme retning og retning..
-
- Opløsning
I dette tilfælde er overførselsprincippet opfyldt, da de to kræfter er af samme størrelse og påføres i samme retning og retning. Alle de nødvendige betingelser i overførselsprincippet er opfyldt. Det kan siges, at de to kræfter er ækvivalente.
-
Fjerde sag
En kraft glider lige i retning af din handling.
-
- Opløsning
I dette tilfælde er princippet om overførbarhed opfyldt, da størrelsen af den anvendte kraft er den samme kraft ikke varierer, og den glider i sin handlingslinje. Igen er alle de nødvendige betingelser for overførselsprincippet opfyldt.
Øvelse 3
To eksterne kræfter påføres et stift legeme. De to kræfter påføres i samme retning og i samme retning. Hvis modulet for det første er 15 N og det andet er 25 N, hvilke betingelser skal en tredje ekstern kraft opfylde for at erstatte resultatet af de to foregående for at opfylde princippet om transmissibilitet??
-
Opløsning
På den ene side skal værdien af den resulterende kraft være 40 N, hvilket er resultatet af tilføjelse af modulet for de to kræfter.
På den anden side skal den resulterende kraft handle på et hvilket som helst punkt på den lige linje, der forbinder de to anvendelsespunkter for de to kræfter..
Referencer
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley.
- Beer, F. 2010. Vektormekanik til ingeniører. McGraw Hill. 5. plads Udgave.
- Giancoli, D. 2006. Fysik: Principper med applikationer. 6. Ed prentice hall.
- Hibbeler, R. 2004. Ingeniørmekanik: Statik. Prentice hall.
- Meriam, J.L. 2012. Ingeniørmekanik: Statik. 7. udgave. Wiley & Sons.



Endnu ingen kommentarer